Games101-2-4 Math
Lecture 02 Review of Linear Algebra
a). Cross Product
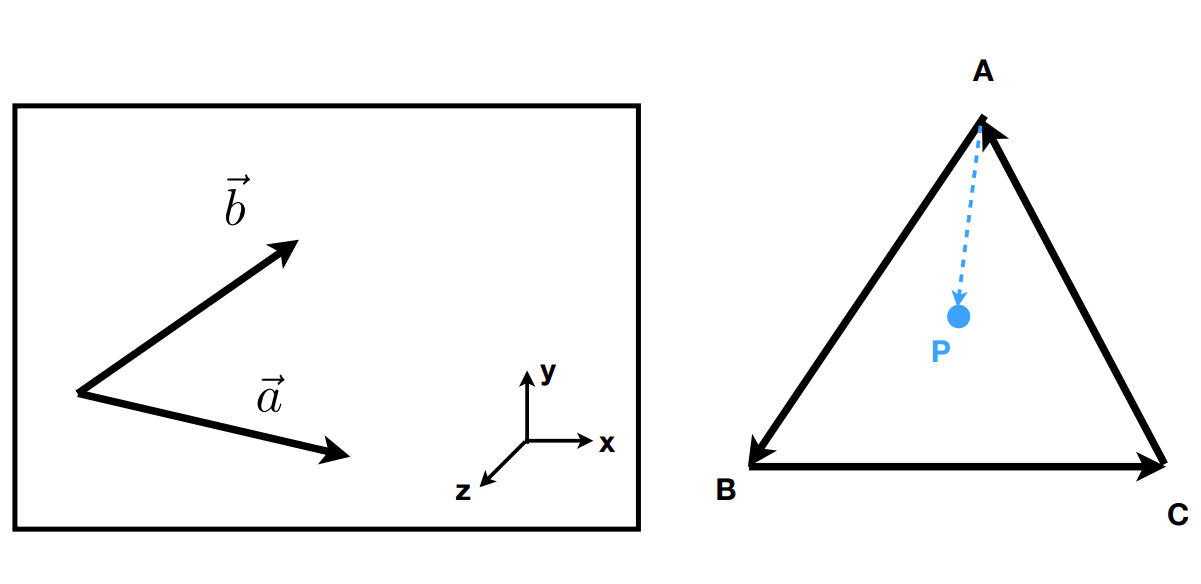
判断相对的左右、前后、内外

判断左右:如$ \vec{a} \cdot \vec{b} > 0$那 $\vec{b}$ 就在 $\vec{a}$ 的左侧(按图中的右手坐标系)
判断内外:判断 $\vec{AB}$ 和 $\vec{AP}$ 的关系,可判断$P$ 点的在 $\vec{AB}$ 的左侧,同理可判断$P$ 在 $\vec{BC}$ 和 $\vec{CA}$ 的左侧,即均在向量同侧。由此,可判断$P$ 点的在 $ABC$ 的内部
b). Orthonormal Coordinate Frames(正交直角坐标系)

Lecture 03 Transformation
a). 2D Transformation
Scale Matrix
Reflection Matrix
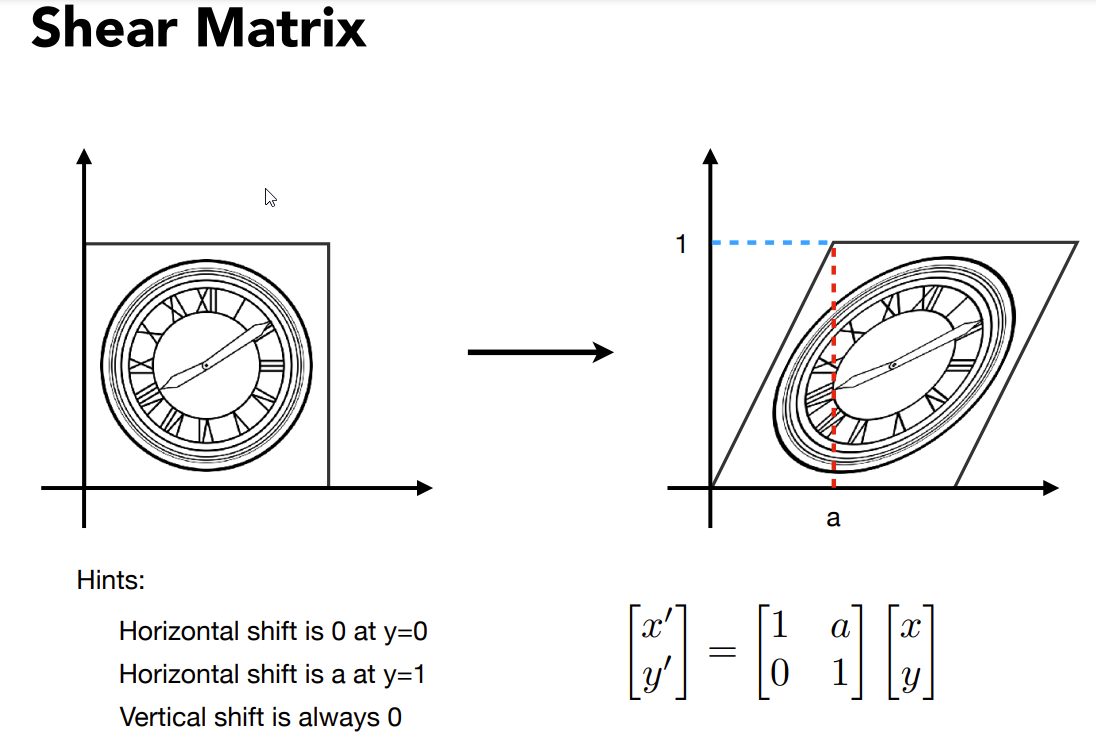
Shear Matrix(切变矩阵)
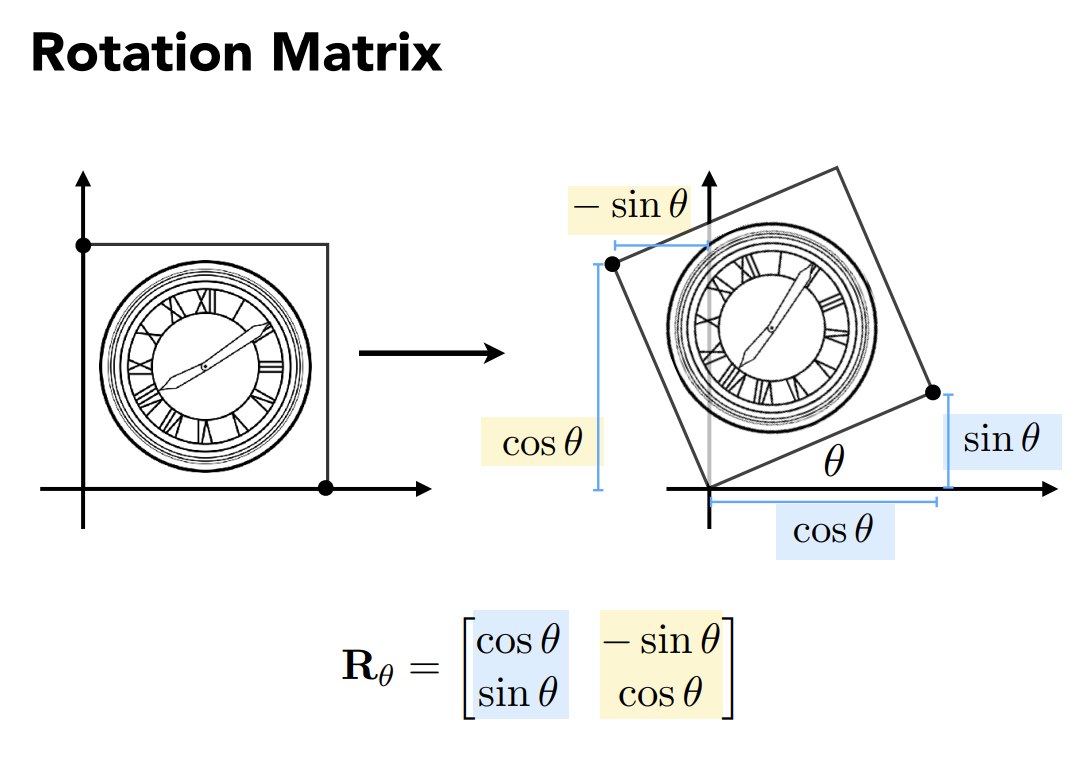
Rotation matrix(默认原点(0, 0), CCW/逆时针旋转)
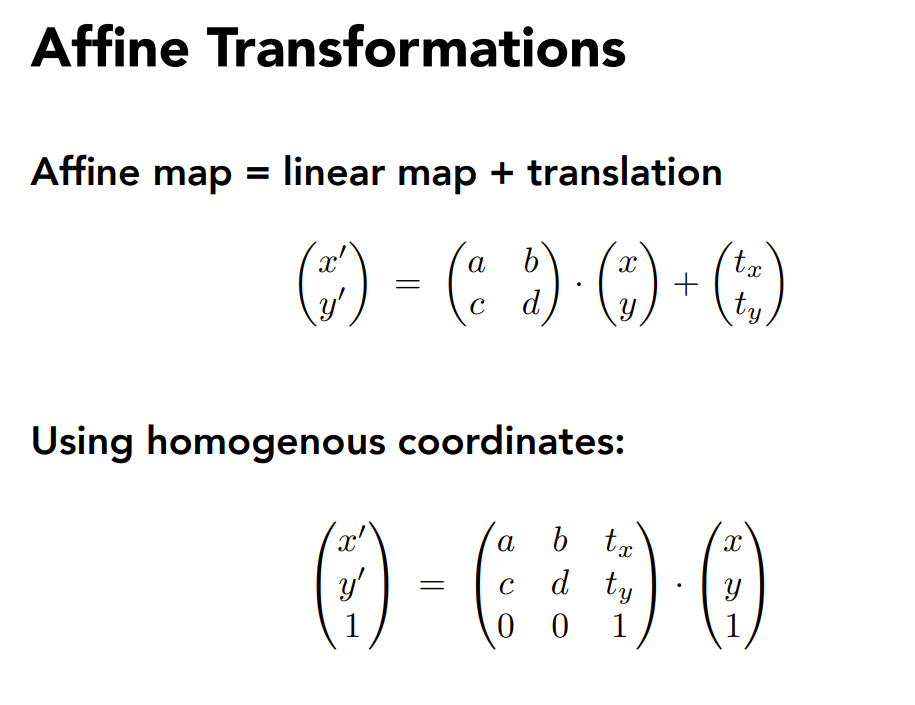
b). Homogeneous coordinates(齐次坐标)
To solve: 平移不是线性变换,无法用2*2矩阵表示(2D)

- 为什么点和向量的其次项不同?
- 向量具有平移不变性,齐次项为0可使其不受$t_x$、$t_y$的影响
- 考虑向量与点、向量/点之间的运算

- point + point得到两点的中点
- 所有的仿射变换(Affine Transformation)都可以用齐次坐标系表示
- 为什么点和向量的其次项不同?
复杂变换,如
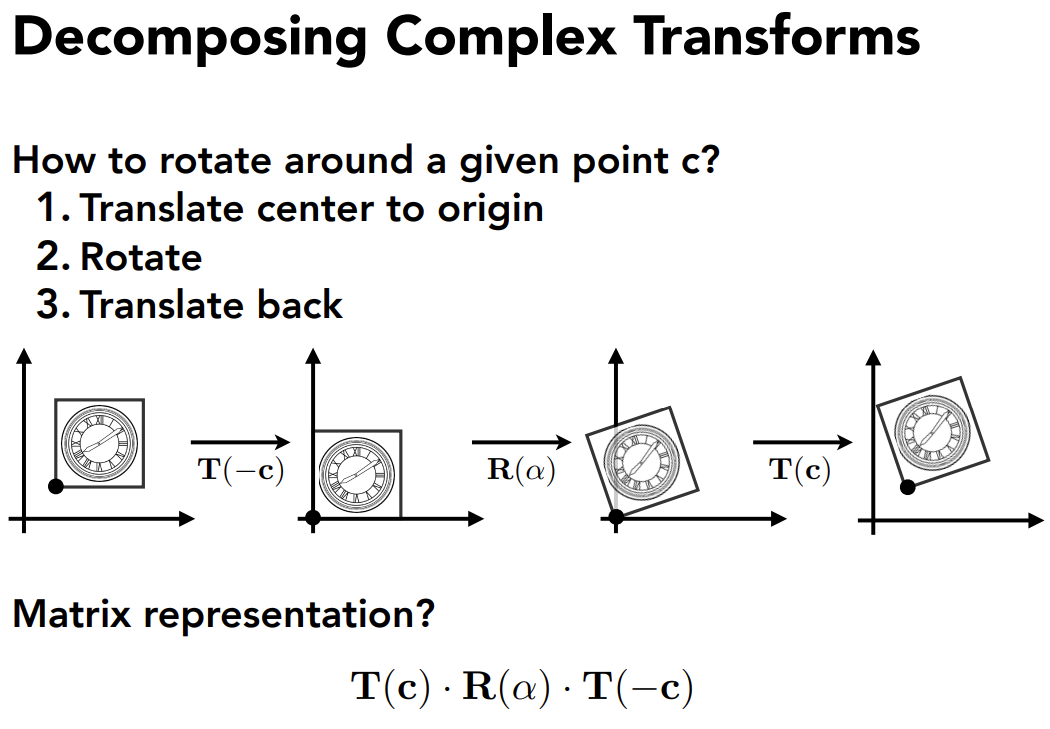
c). 3D Transformation

- 三维空间中使用齐次坐标的变换
上述矩阵先线性变换再平移,相当于:
- 补充知识:正交矩阵
Lecture 04 Transformation Cont.
a). 3D变换
a.1) Scale、Translation

a.2) 3D Rotations
旋转矩阵:
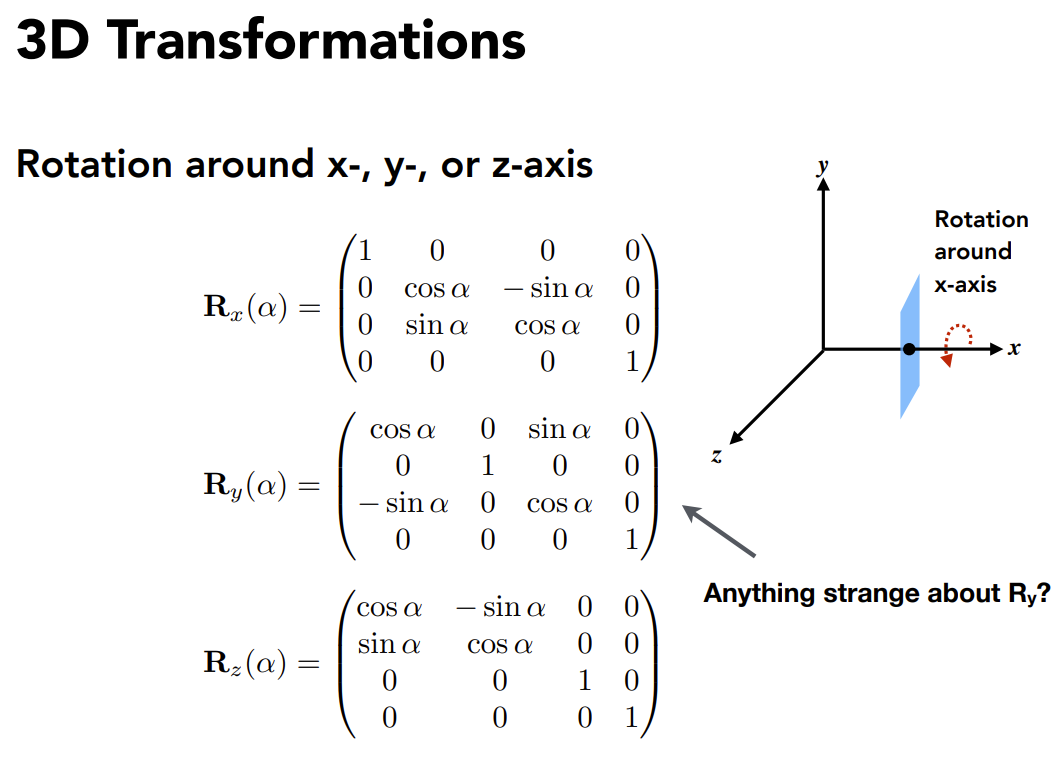
注意绕y轴旋转和其他的区别($y=cross(z, x)$)
三轴旋转可以表示3D空间的所有旋转变换,例如飞机(Roll、Pitch、Yaw)
罗德里格旋转公式(表示绕任意经过原点轴的任意旋转)
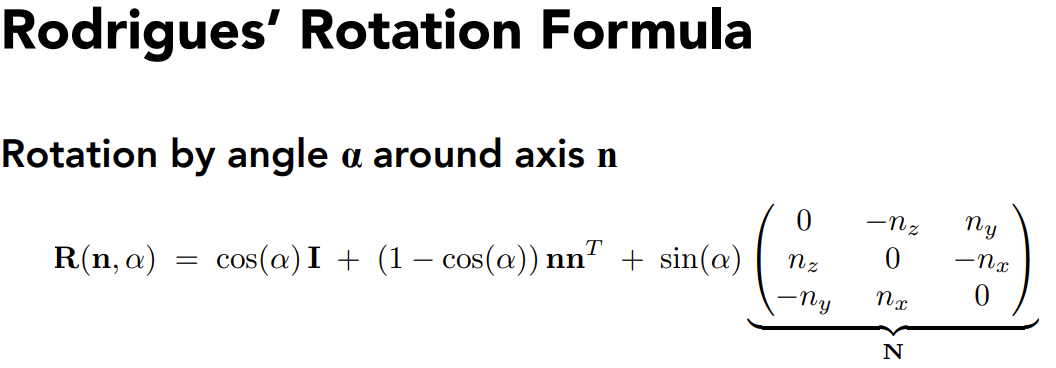
- 默认旋转轴经过原点
- $\left(\begin{array}{ccc}
0 & -n_{z} & n_{y} \\
n_{z} & 0 & -n_{x} \\
-n_{y} & n_{x} & 0
\end{array}\right)$是叉乘向量的矩阵形式 - 四元数多是为了旋转之间的插值用的
- 四元数待课后补充
b). Viewing Transformation
- 概念:Viewing Transformation(观测矩阵)相当于MVP中的VP
- View/Camera transformation
- Projection transformation
- Orthographic projection
- Perspective projection
b.1) View Transformaiton

Difine the camera:
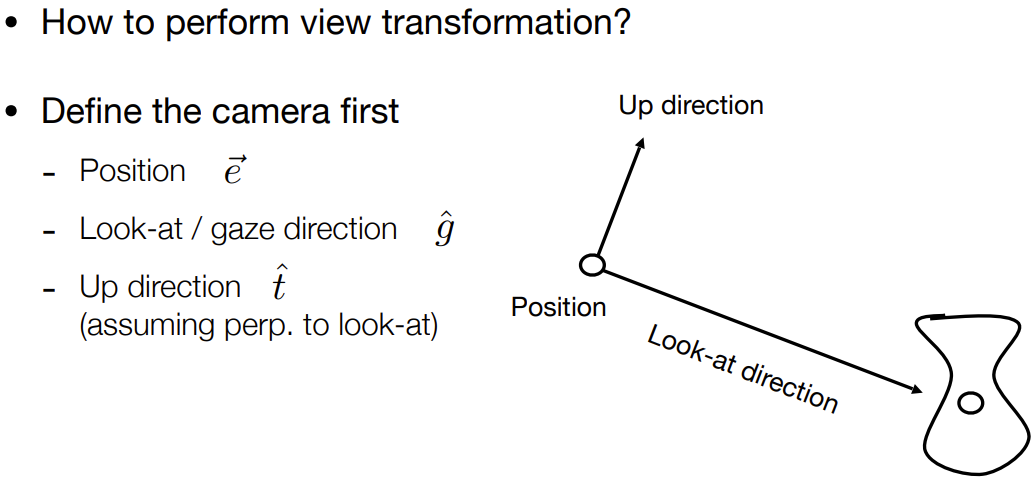
View Space:
- 相机位于原点,上是$Y$,看向$-Z$
- 看成所有相机不动,全是其他物体动
- $M_{view}$:
- in math:
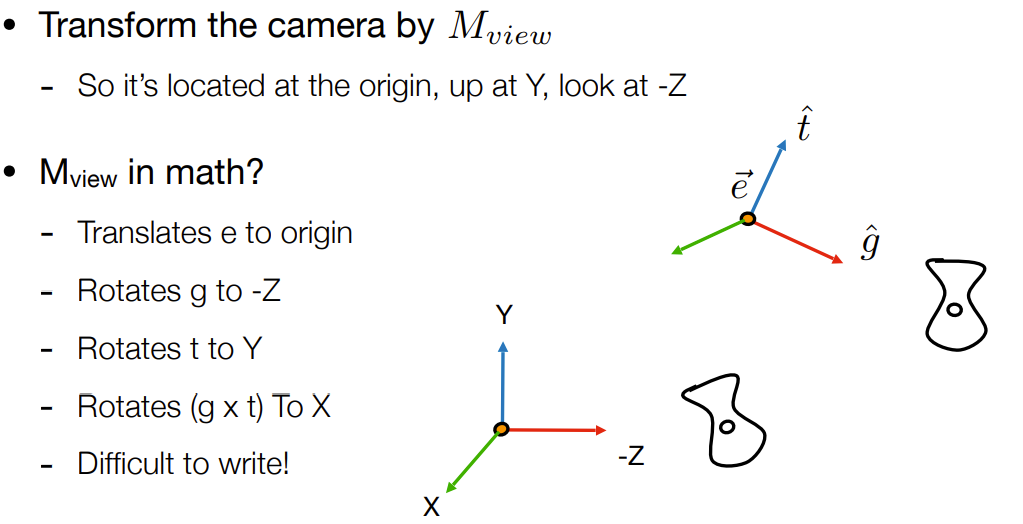

- 直接应用矩阵空间变换
- in math:
b.2) Projection transformation
这里的投影变换中对xyzw都乘了z,因此最后需要齐次除法(透视除法),转换到NDC(Normalized Device Coordinates)
b.2.1 Orthographic Projection
简易理解:
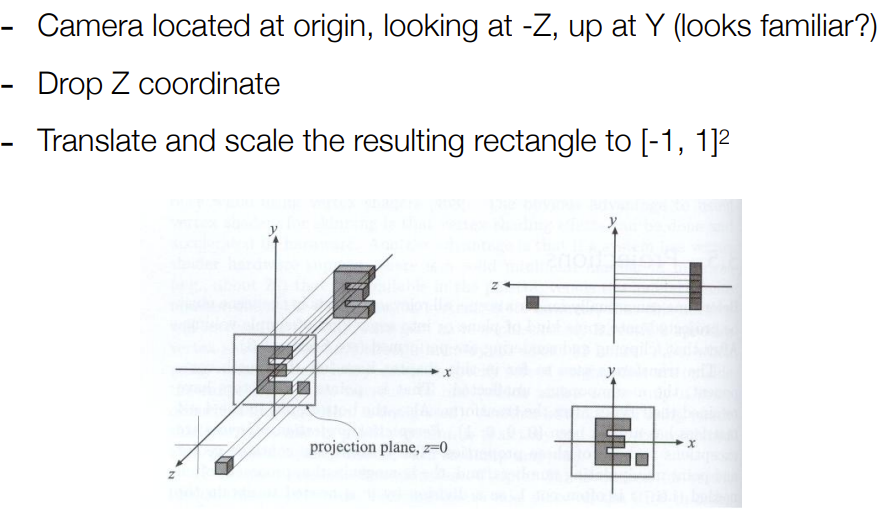
- 注意$[-1, 1]$
图形学中的做法:
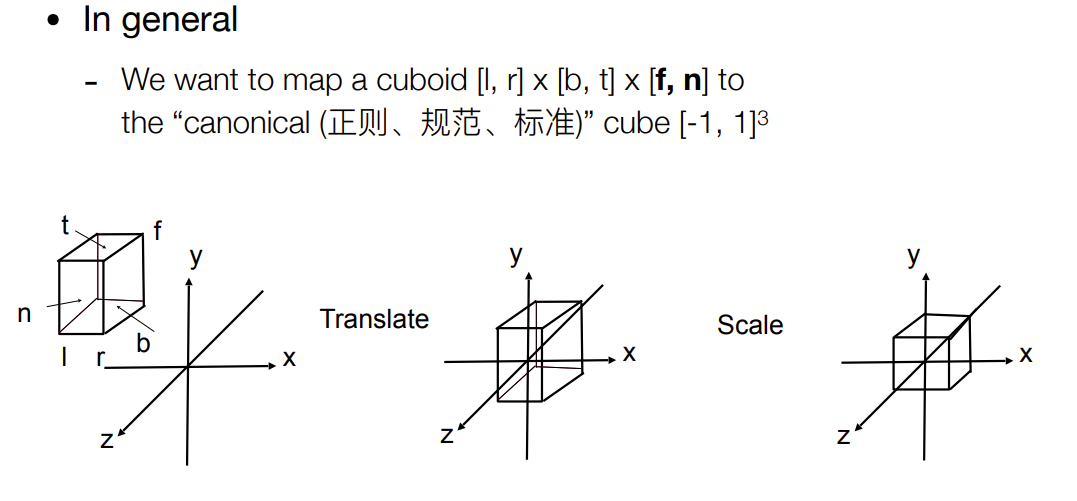
- 通过平移将立方体中心化
- 缩放成标准立方体(“canonical” cube)
- 这里采用右手坐标系,缺点是$f<n$,远的z值小于近的z值
矩阵形式:
Caveat:
- (使用右手坐标系)看向 $-Z$ 使得$f<n$,远的z值小于近的z值
- 这也是为什么OpenGL使用左手坐标系(但也会造成其他问题)
b.2.2 Perspective Projection
前置知识:
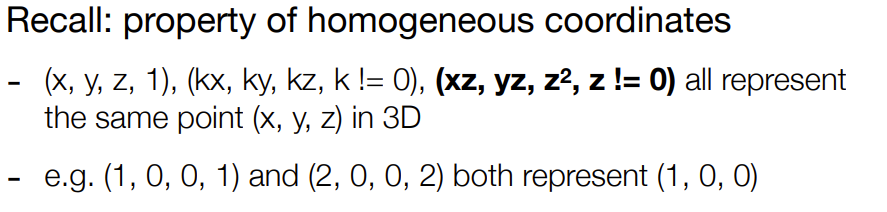
How to do perspective projection
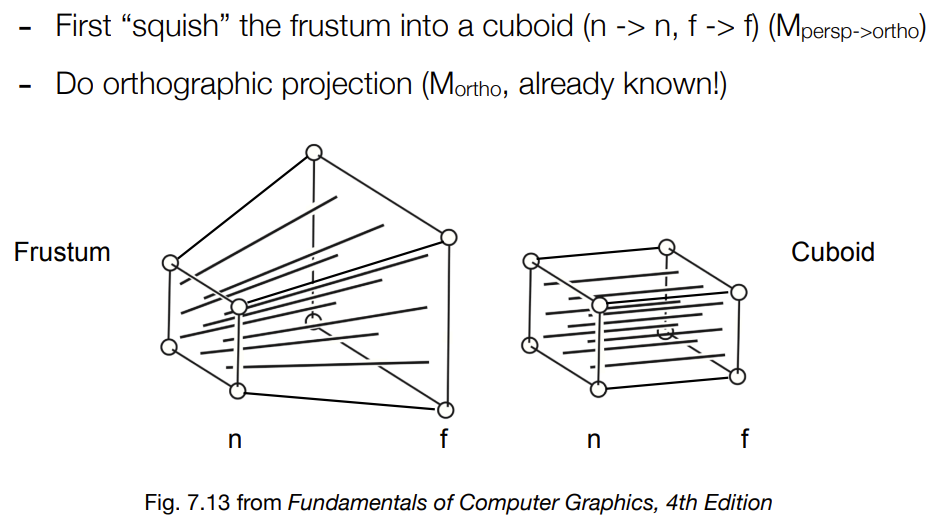
挤压(squish)

- $M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{array}\right)$ - 不知道经过挤压后$z$的变化(即第三行乘以$\left(\begin{array}{l}
x \\
y \\
n \\
1
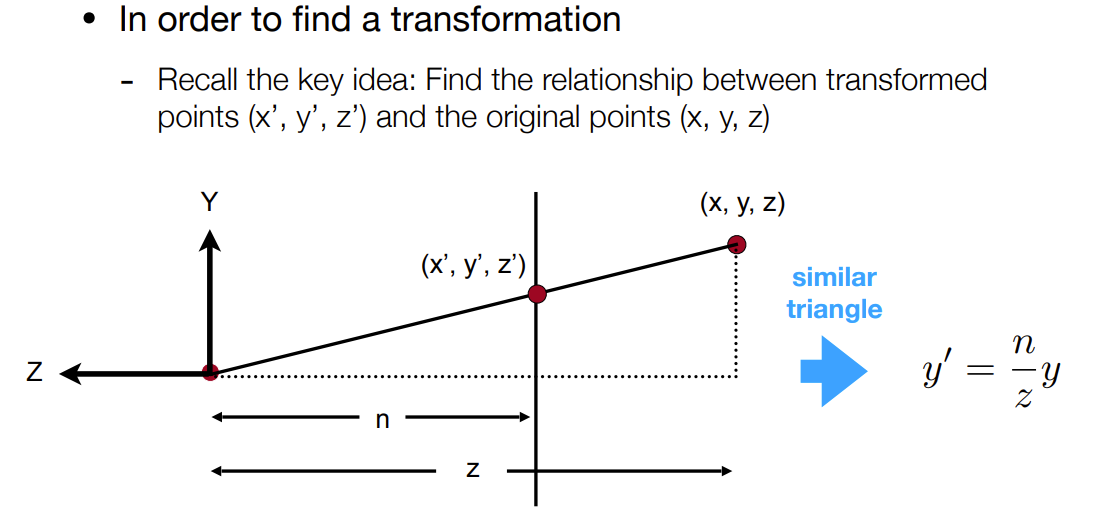
\end{array}\right)$未知),但知道:- 在近平面的点不会变化
- 在远平面的中点不会变化
- $z=n$时,$\left(\begin{array}{l}
x \\
y \\
n \\
1
\end{array}\right) \Rightarrow\left(\begin{array}{l}
x \\
y \\
n \\
1
\end{array}\right)==\left(\begin{array}{c}
n x^{n} \\
n y \\
n^{2} \\
n
\end{array}\right)$- 易得$\left(\begin{array}{llll}
0 & 0 & A & B
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
n \\
1
\end{array}\right)=n^{2}$ - $An+B=n^2$
- 易得$\left(\begin{array}{llll}
- $z=f$时,对于远平面中点,$\left(\begin{array}{l}
0 \\
0 \\
f \\
1
\end{array}\right) \Rightarrow\left(\begin{array}{l}
0 \\
0 \\
f \\
1
\end{array}\right)==\left(\begin{array}{c}
0 \\
0 \\
f^{2} \\
f
\end{array}\right)$- 易得$\left(\begin{array}{llll}
0 & 0 & A & B
\end{array}\right)\left(\begin{array}{l}
0 \\
0 \\
f \\
1
\end{array}\right)=f^{2}$ - $Af+B=f^2$
- 易得$\left(\begin{array}{llll}
得$A=n+f$,$B=-nf$
$M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right)$之后进行平行投影的变换,得
$\mathbf{M}_{\text {per }}=\left[\begin{array}{cccc}
\frac{2 n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\
0 & \frac{2 n}{t-b} & \frac{b+t}{b-t} & 0 \\
0 & 0 & \frac{f+n}{n-f} & \frac{2 f n}{f-n} \\
0 & 0 & 1 & 0
\end{array}\right]$
- $M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
【补充】
作业1中用到的绕任意轴旋转:
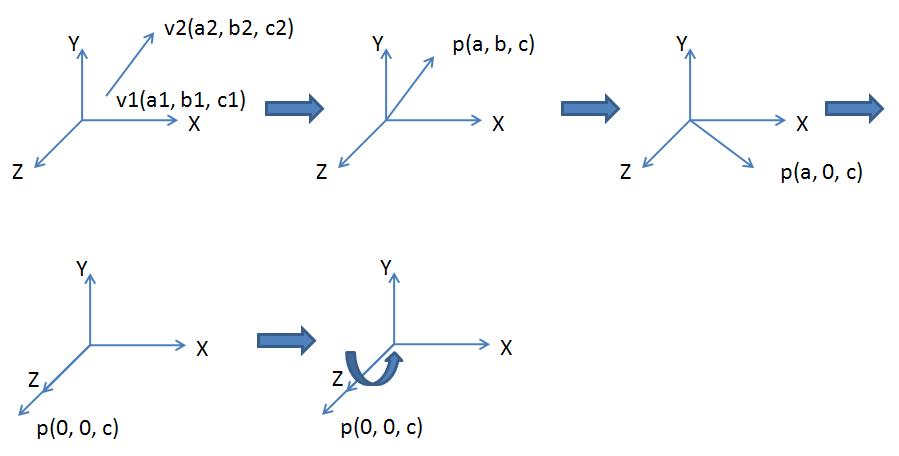
- 步骤:
- 将旋转轴平移至原点
- 将旋转轴旋转至YOZ平面
- 将旋转轴旋转至于Z轴重合
- 绕Z轴旋转θ度
- 执行步骤3的逆过程
- 执行步骤2的逆过程
- 执行步骤1的逆过程
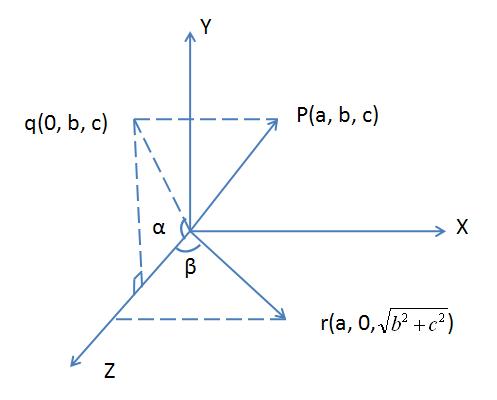
如果旋转轴是过原点的,那么第一步和最后一步的平移操作可以省略,也就是把中间五个矩阵连乘起来,再转置一下,得到下面的绕任意轴旋转的矩阵