Games101-5-6 Rasterization

发表于 更新于 分类于 阅读次数：

Lecture 05 Rasterization(Triangles)

a). Perspective Projection

  • 如何定义一个frustum：

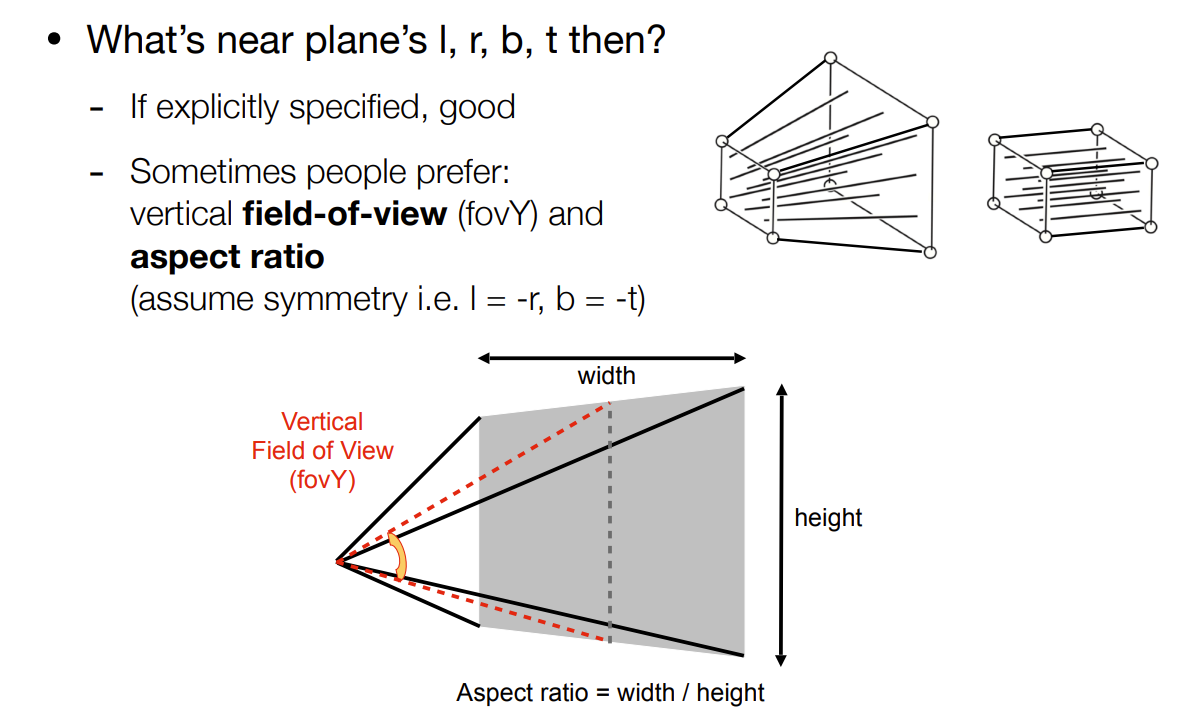
    Frustum

    • 近平面宽度、高度（得到宽高比）
    • FOV(Field of View)

b). Viewport transformation

  • 经过MVP后，模型空间中点变换到标准立方体（canonical cube, x,y,z[-1, 1]）中。之后就需要进行视口变换（Viewport transformation）

  • 定义屏幕空间

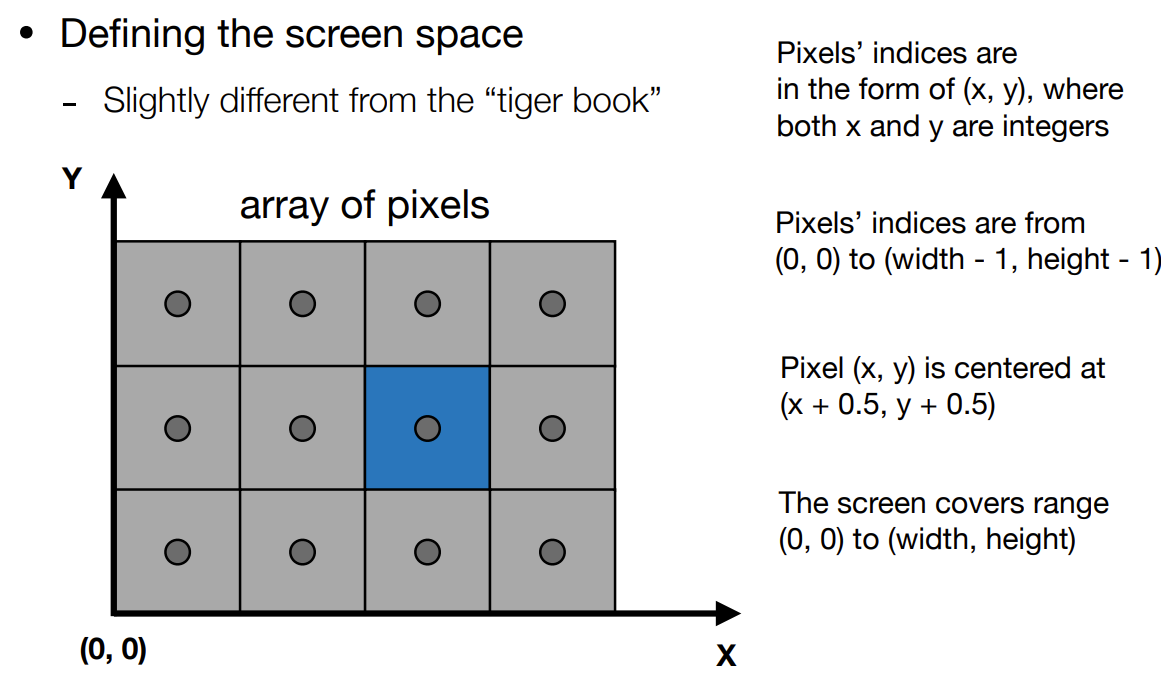
    Difine_the_screen_space

    • OpenGL屏幕空间坐标原点为左下（上图），DX坐标原点为左上
    • 像素位置该像素（方块）左下角的坐标，如左下角像素坐标为$(0, 0)$，但像素中心为$(0.5, 0.5)$

  • Viewport transformation

    ScreenSpace_transformation

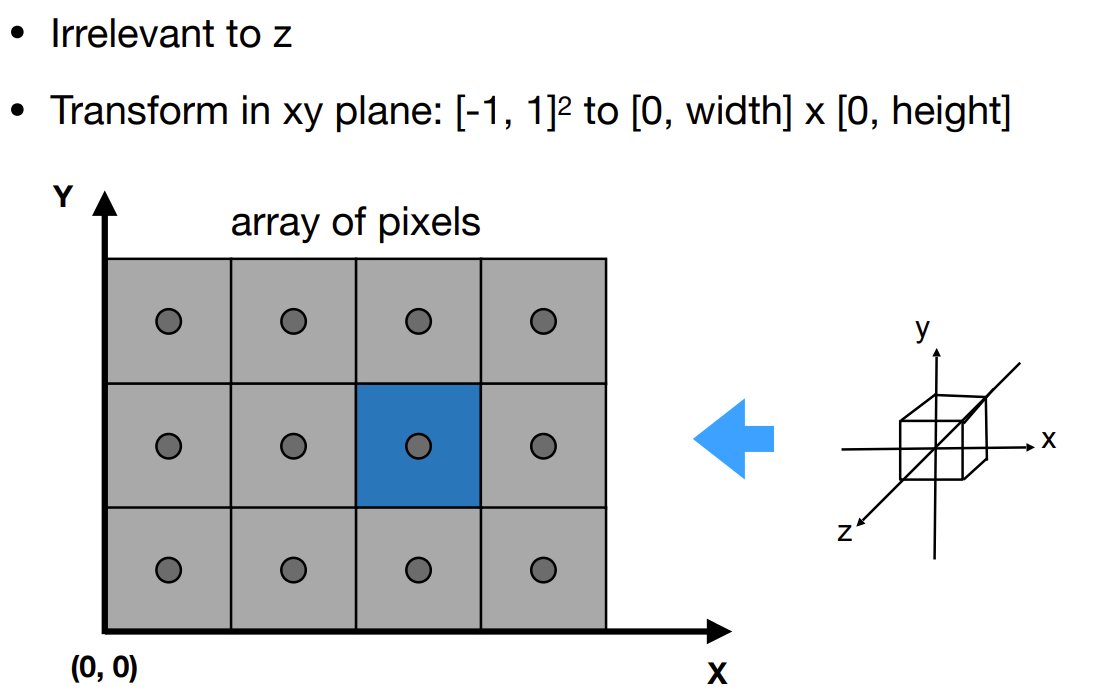
c). Rasterization

  • Frame Buffer: Memory for a Raster Display

    • 显存中的一块区域

    • 补充：Render texture（详情见Other/Note）

      • 以下以Unity为例：

        渲染过程中，贴图最开始在CPU内存，这时的贴图被称为client-side的texture，最后被送到GPU，这时叫server-side的texture；

        Render texture是将FrameBufferObject连接到一个server-side的texture；

        • 注意：FrameBufferObject不一定只有一个，也不一定连接屏幕；

        详情：http://t.csdn.cn/3JHqA

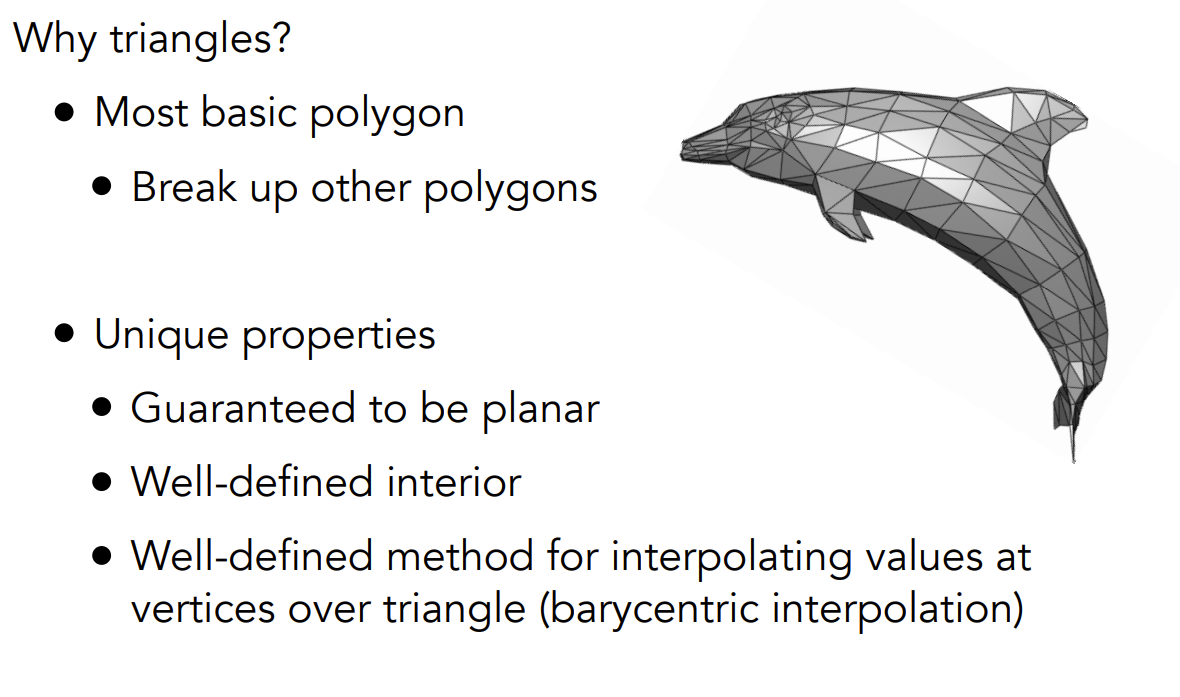
  • Triangles - Fundamental Shape Primitives

    • 无法分割为其他多边形
    • 保证是一个平面
    • 容易区分内部和外部
    • 内部插值方便
    • Triangles

  • Fundament： What Pixel Values Approximate a Triangle?T2PV

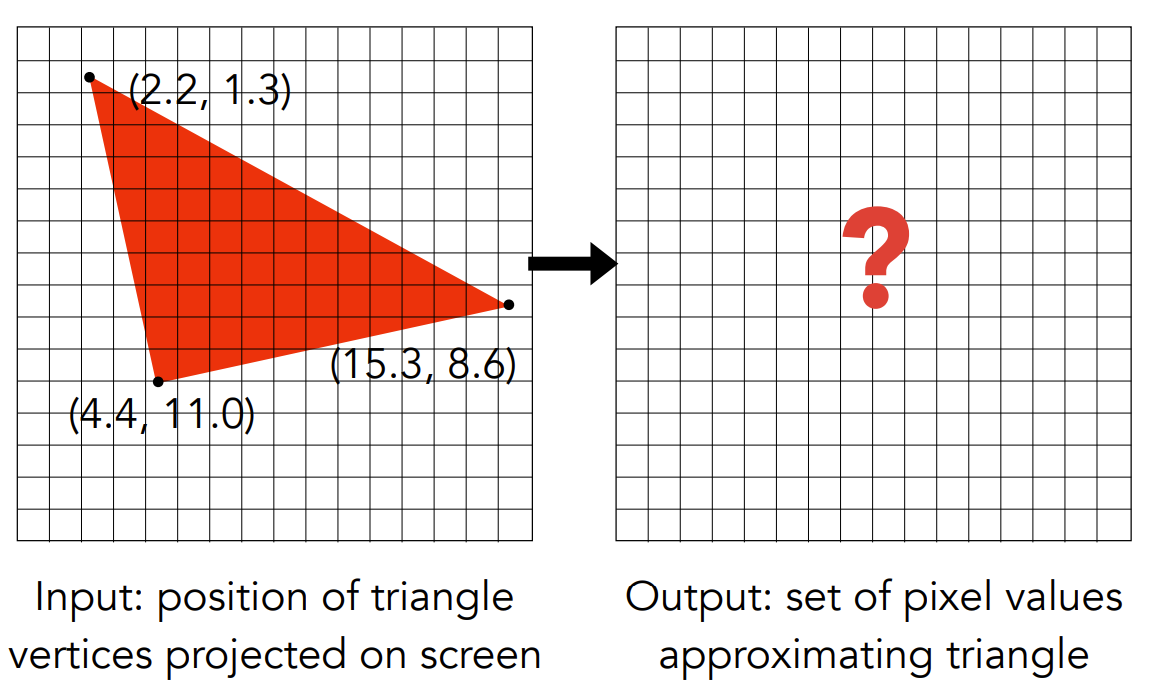
    • Sampling（采样）：逐像素中心采样，判断像素是否在三角形内

      • for (int x = 0; x < xmax; ++x)
 output[x] = f(x);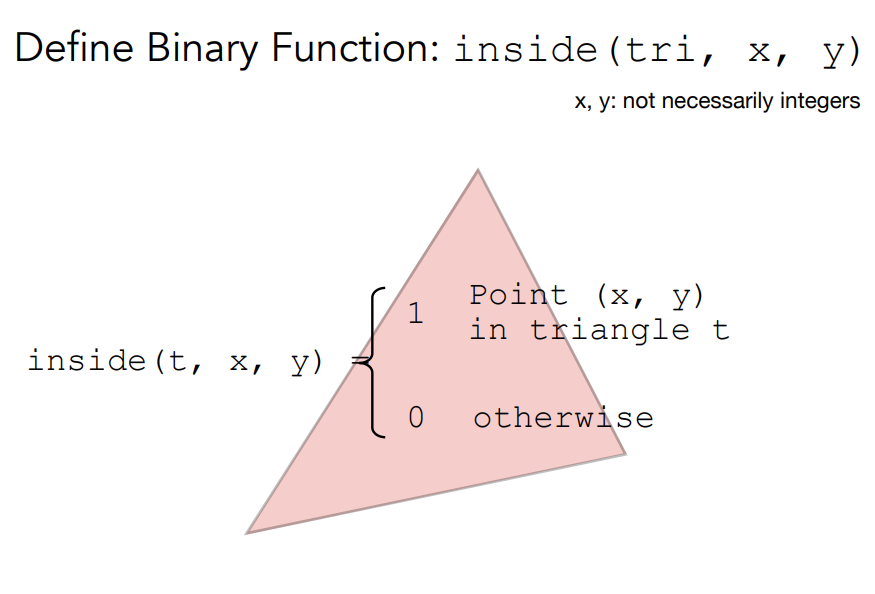

      • if_PinT

    • 判断$(x,y)$是否在三角形内：做三次叉乘，看正负符号是否相同，相同则在三角形内；

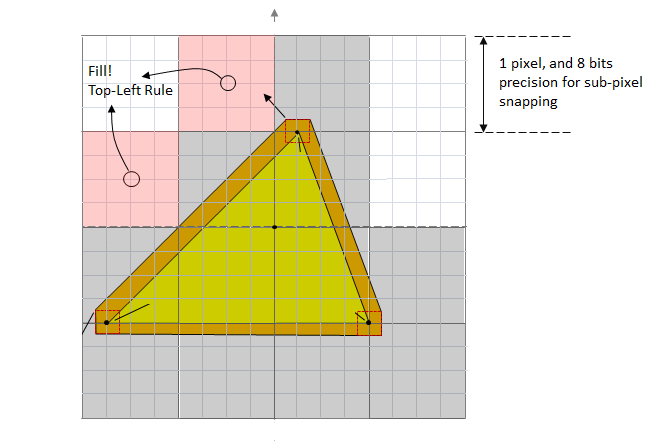
    • Edge Cases：要么不做处理，要么特殊处理（OpenGL，DX里规定落于左边和上边算三角形中的点，而落于右边和下边的不算“Top-Left Rule“）Top_left_rule

  • 光栅化加速

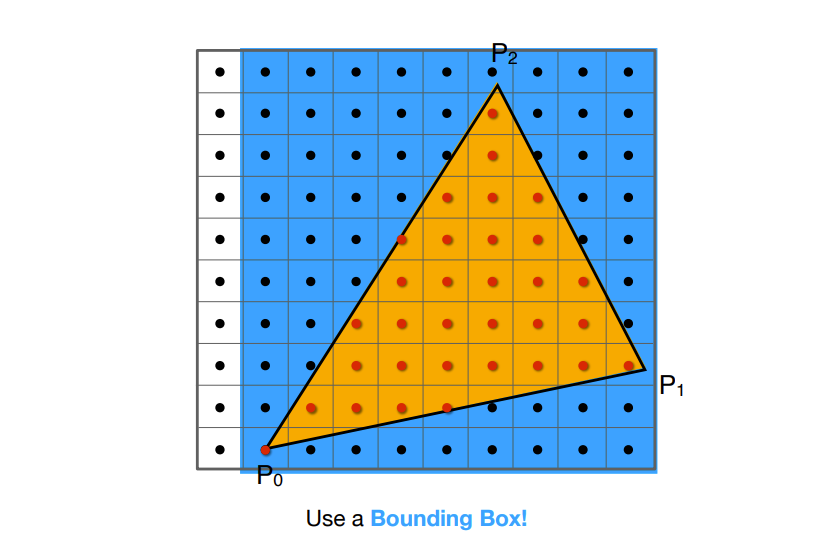
    • 光栅化中，对每一个像素都判断是否在三角形中性能浪费过大。因此，加入Bounding Box（包围盒）来限定需要进行判断的区域BoundingBox
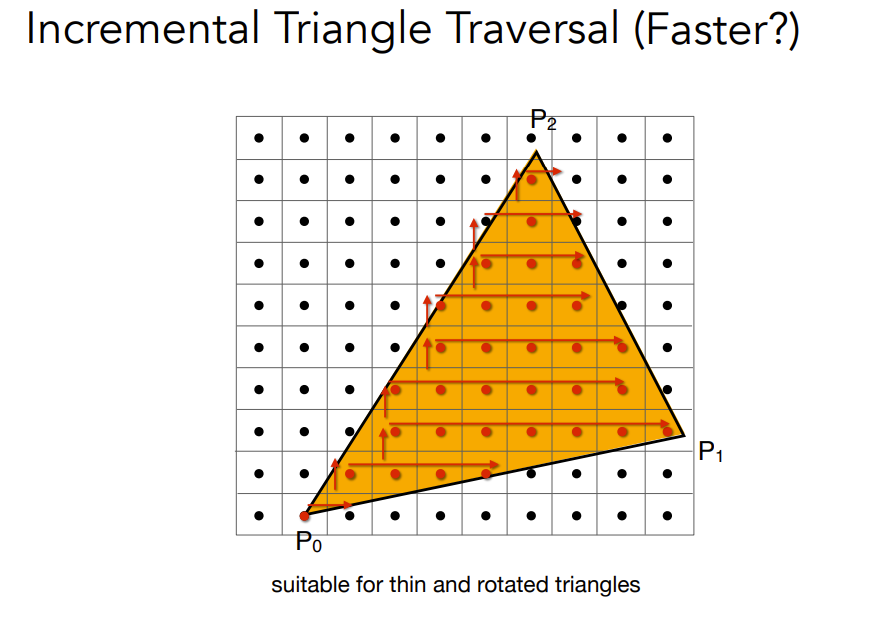
    • Incremental Triangle Traversal（找到三角形中每一行最左和最右的像素，但实际上没那么容易，是用于细长并旋转的三角形）Incremental_Triangle_Traversal

Lecture 6: Rasterization 2(Antialiasing and Z-Buffering)

a). Sampling Artifacts(Errors / Mistakes / Inaccuracies) in Computer Graphics

  • 由于采样造成的“Artifacts“
    • 锯齿（ Jaggies）——空间上采样
    • 摩尔纹（Moire）——欠采样图像
    • 车轮错觉（Wagon wheel effect）——时间上采样
    • ……
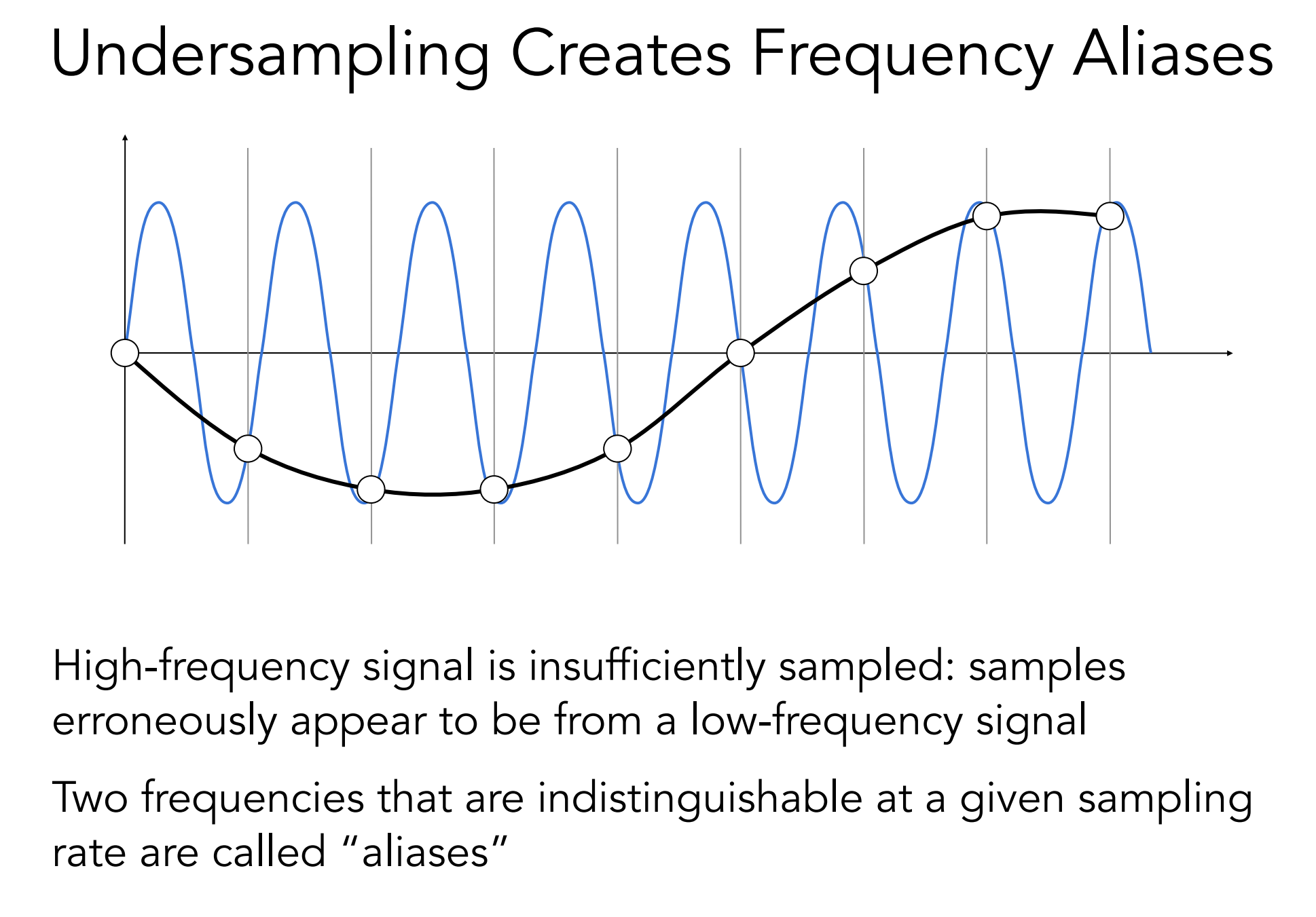
  • 造成错误的原因：信号频率高，而采样频率低（可联系奈奎斯特定理：当采样频率大于信号中最高频率的2倍时(fs>2f)，采样之后的数字信号完整地保留了原始信号中的信息）

b). Antialiasing Idea:Blurring (Pre-Filtering) Before Sampling

  • 抗锯齿的思路就是在采样前”模糊“；

    AS

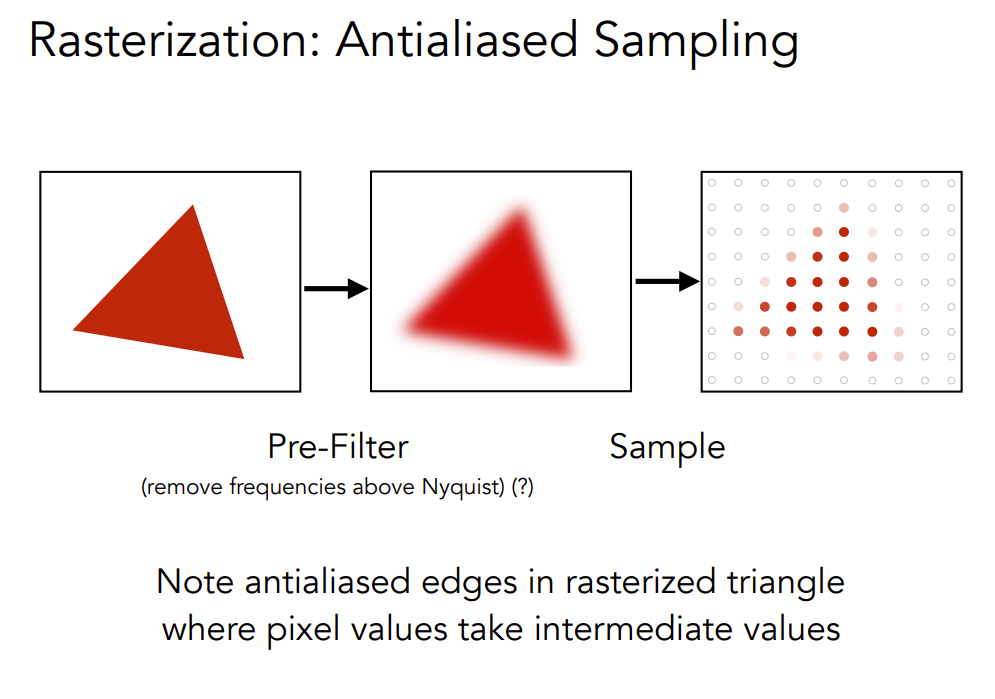
    • 注意：先模糊，后采样。对应频域上先低通滤波（或其他操作，如卷积、超采样，FSAA那种图像层面的抗锯齿暂不考虑），后采样（卷积定理：时域信号与冲激信号相乘，等于两者对应的频域信号卷积。反之，也成立）；

c). Frequency Domain

c.1). Fundamental

  • 傅里叶变换

  • 卷积定理：时域中乘积等于频域上卷积，反之也成立。（时域信号与冲激信号相乘，等于两者对应的频域信号卷积。反之，也成立。）

  • Aliases: 在给定的采样率下，无法区分两个不同频率Aliases

c.2). Filtering: Getting rid of certain frequency contents

  • K空间：反应图像进过二维傅里叶变换后的结果，越靠中间，频率越小；K_space
    • 出现十字星的原因：把图像看成类似Wrap Mode的Repeat，即重复的图像。使得其四个方向的高频内容增加，形成十字星；
  • Filter（滤波器）：
    • High-pass filterHigh_pass filter
    • Low-pass filterLow_pass_filter
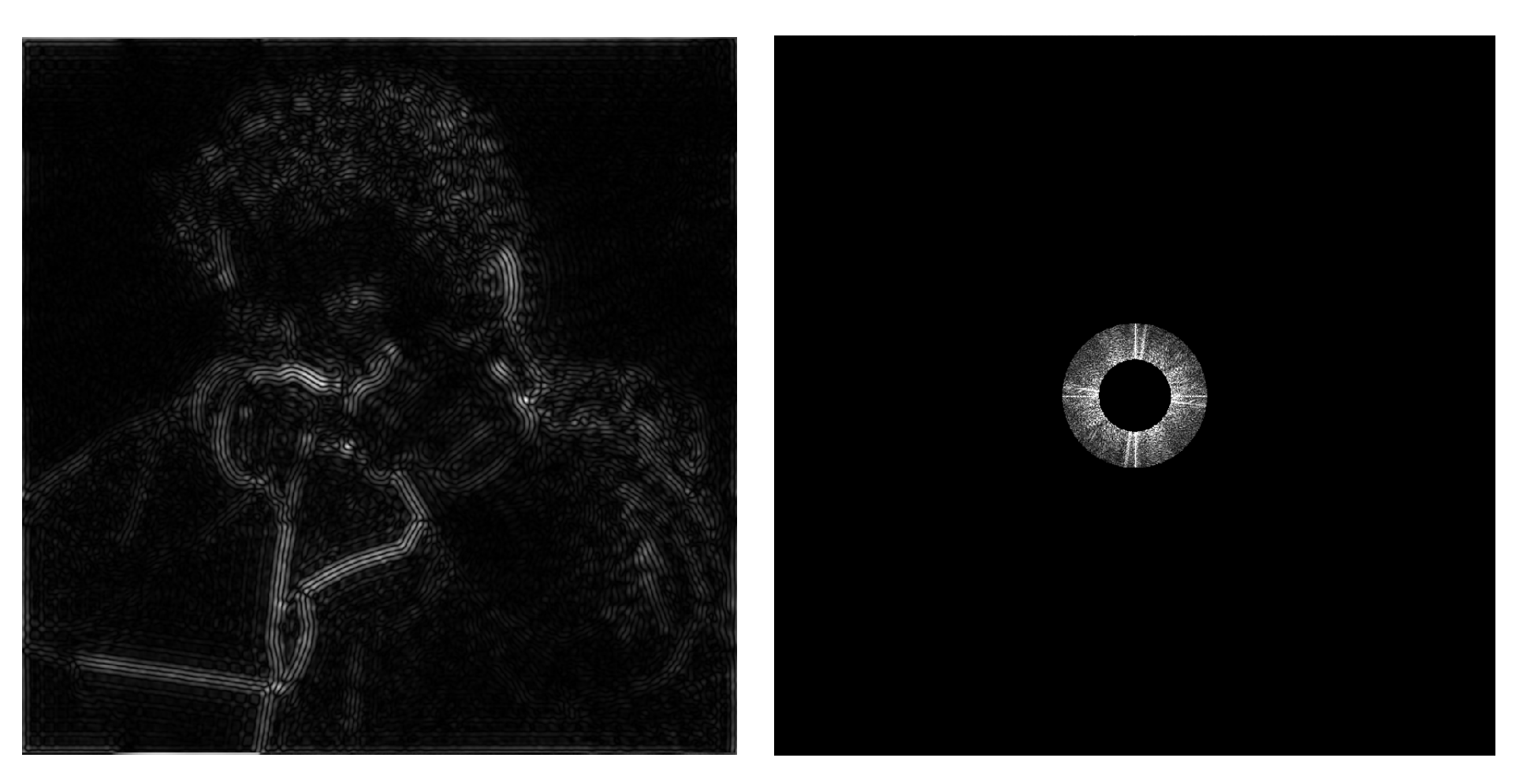
    • Filter Out Low and High FrequenciesF_Low_and_high

c.3). Convolution

  • Filtering = Convolution (= Averaging)
    • 注意：只是在这里相等，而滤波和卷积概念上不相同；
  • 对信号进行滤波，就是用卷积核和信号做卷积；
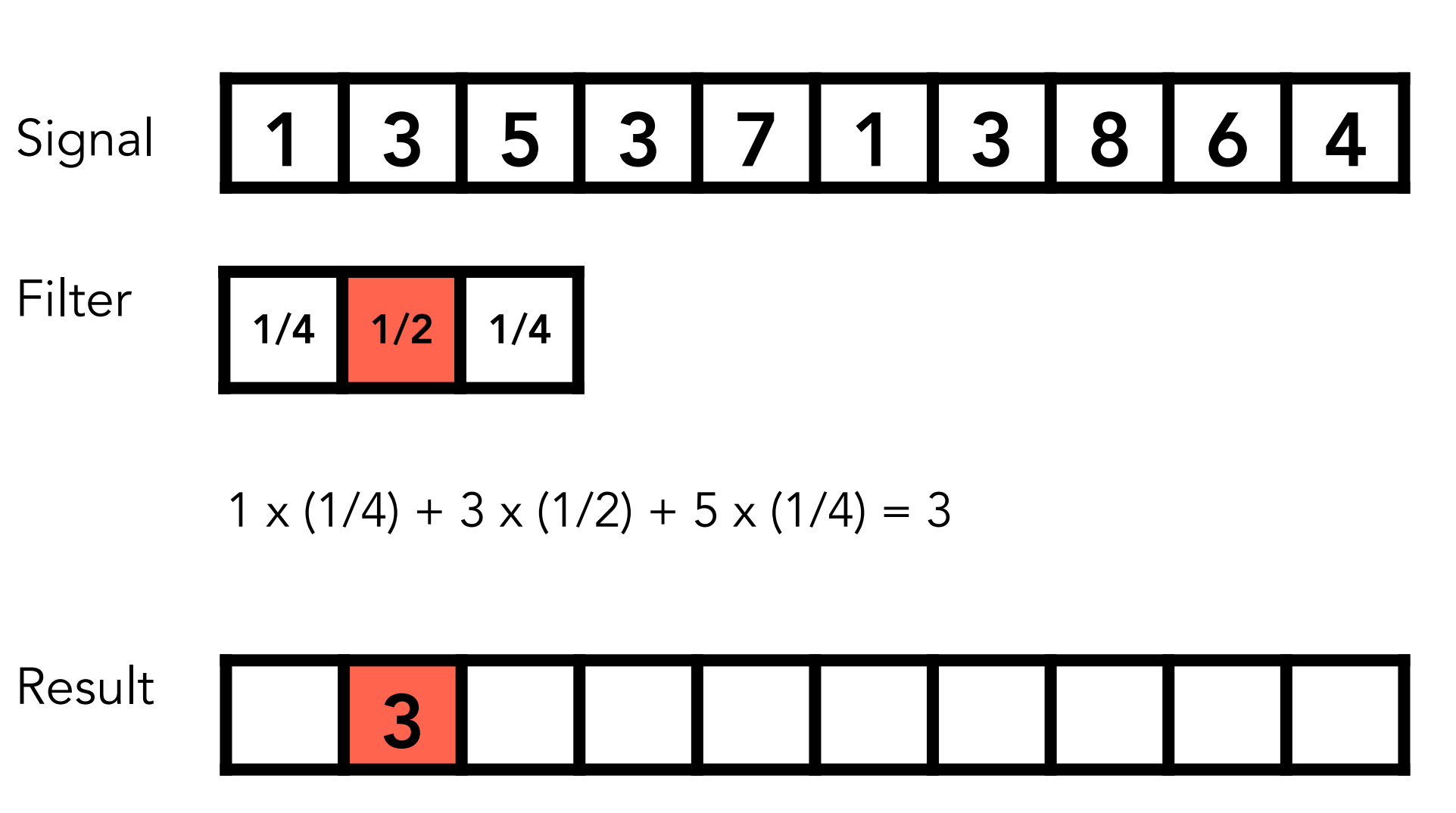
    • Point-wise local averaging in a “sliding window”convolution
  • 卷积定理：在空域（时域）做卷积，等于在频域做乘积；反之亦然。
    • 因此，对图像滤波有两种处理方法；
      • Option 1: 在空域上与滤波器（卷积核）做卷积；
      • Option 2:
        1. 将图像和滤波器（卷积核）转换到频域（傅里叶变换）；
        2. 两者在频域相乘；
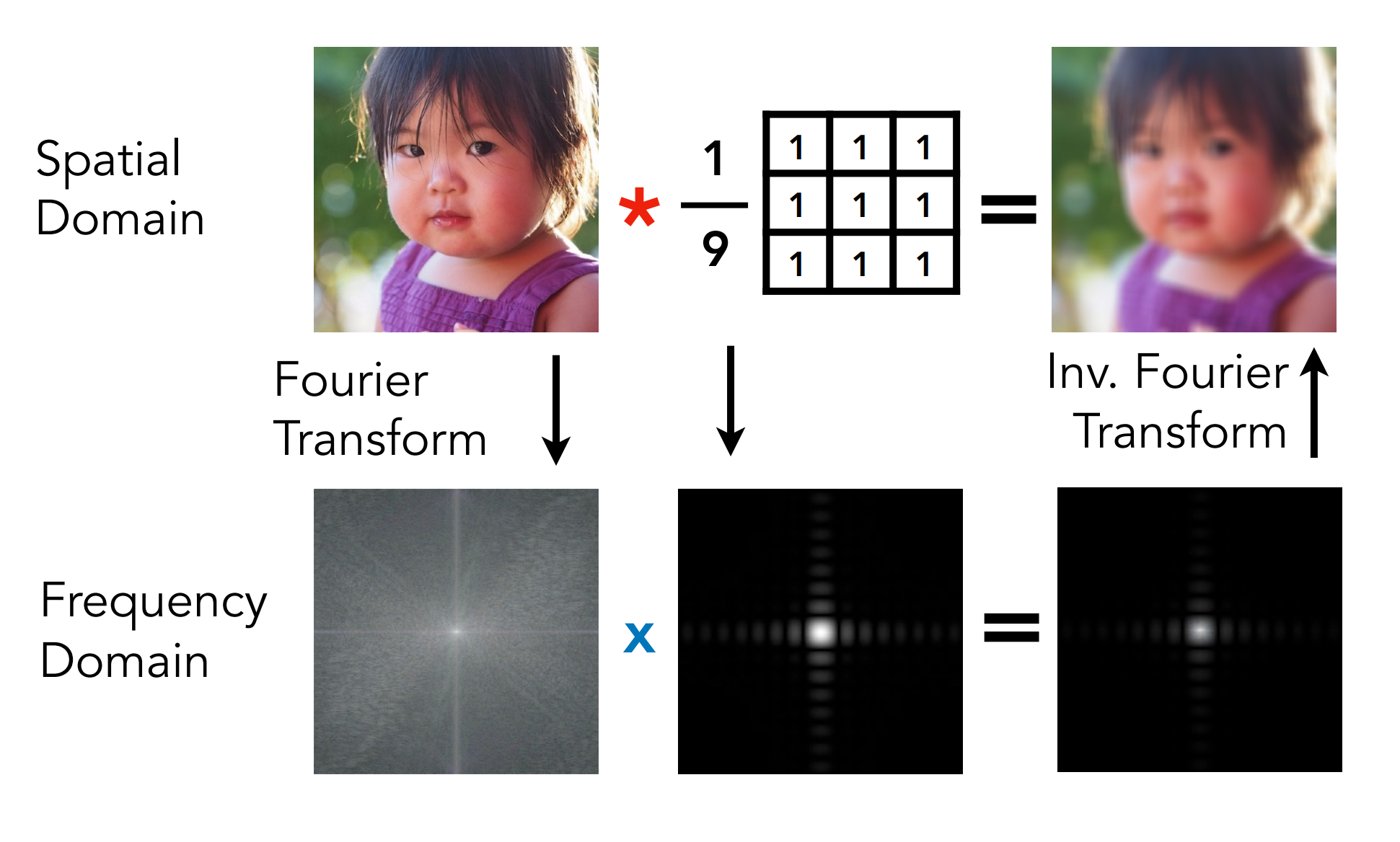
        3. 将得到的结果重新变换到空域（逆傅里叶变换）；Convolution_Theorem
  • Box FilterBoxFilter
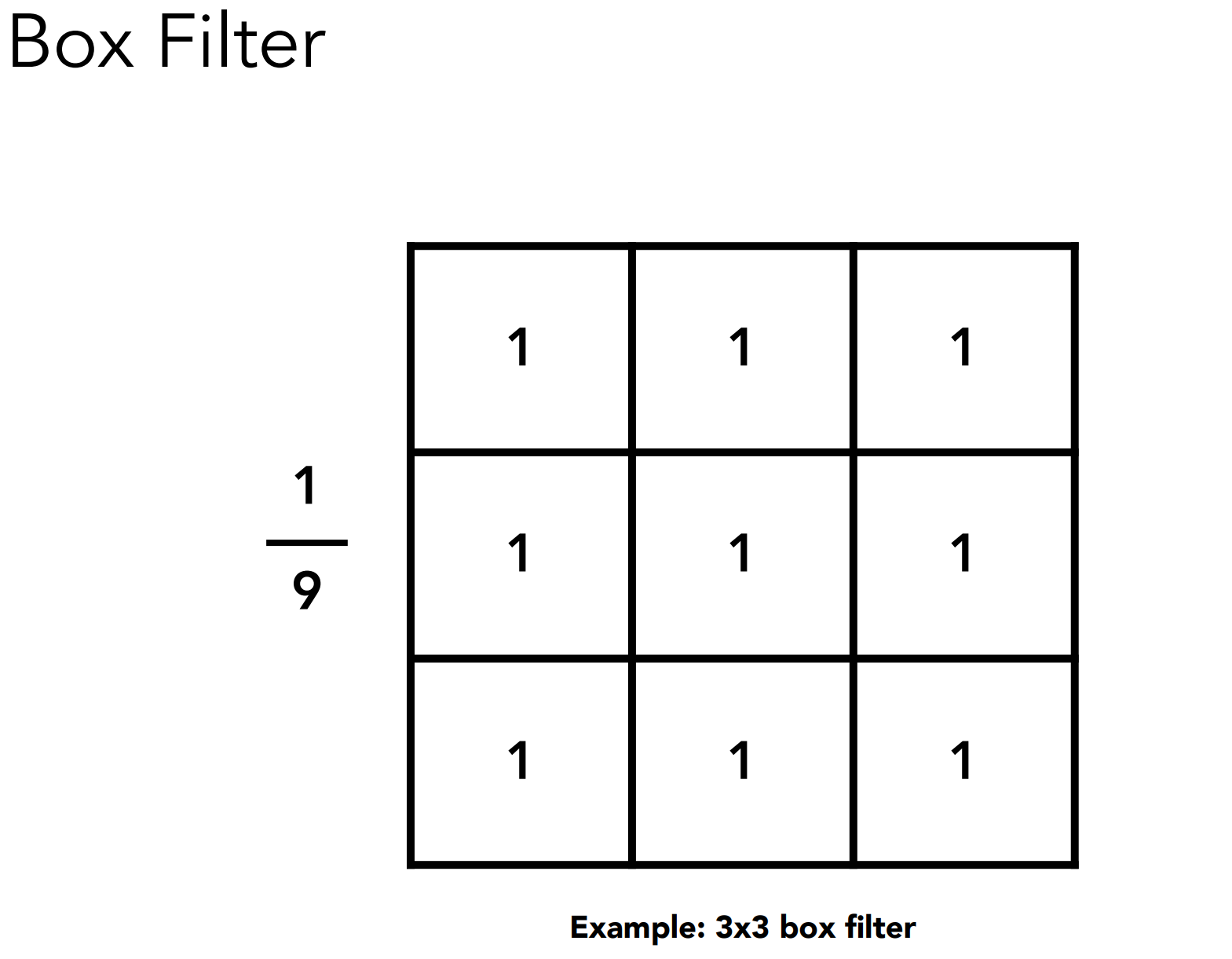
    • 箱式滤波类似于低通滤波BoxF_LP
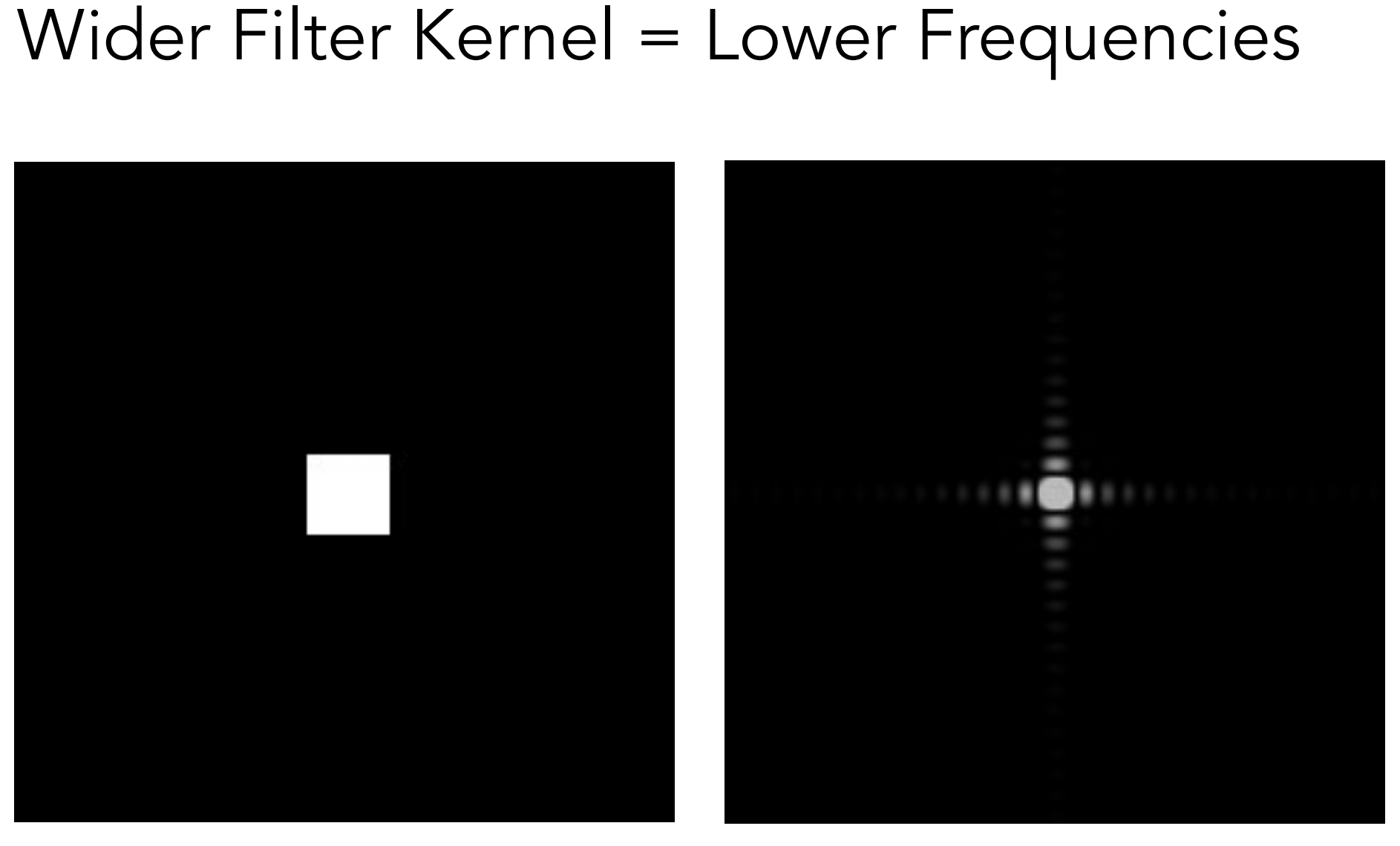
    • 更大的卷积核意味着更低的频率WiderFK

c.4). Sampling = Repeating Frequency Contents

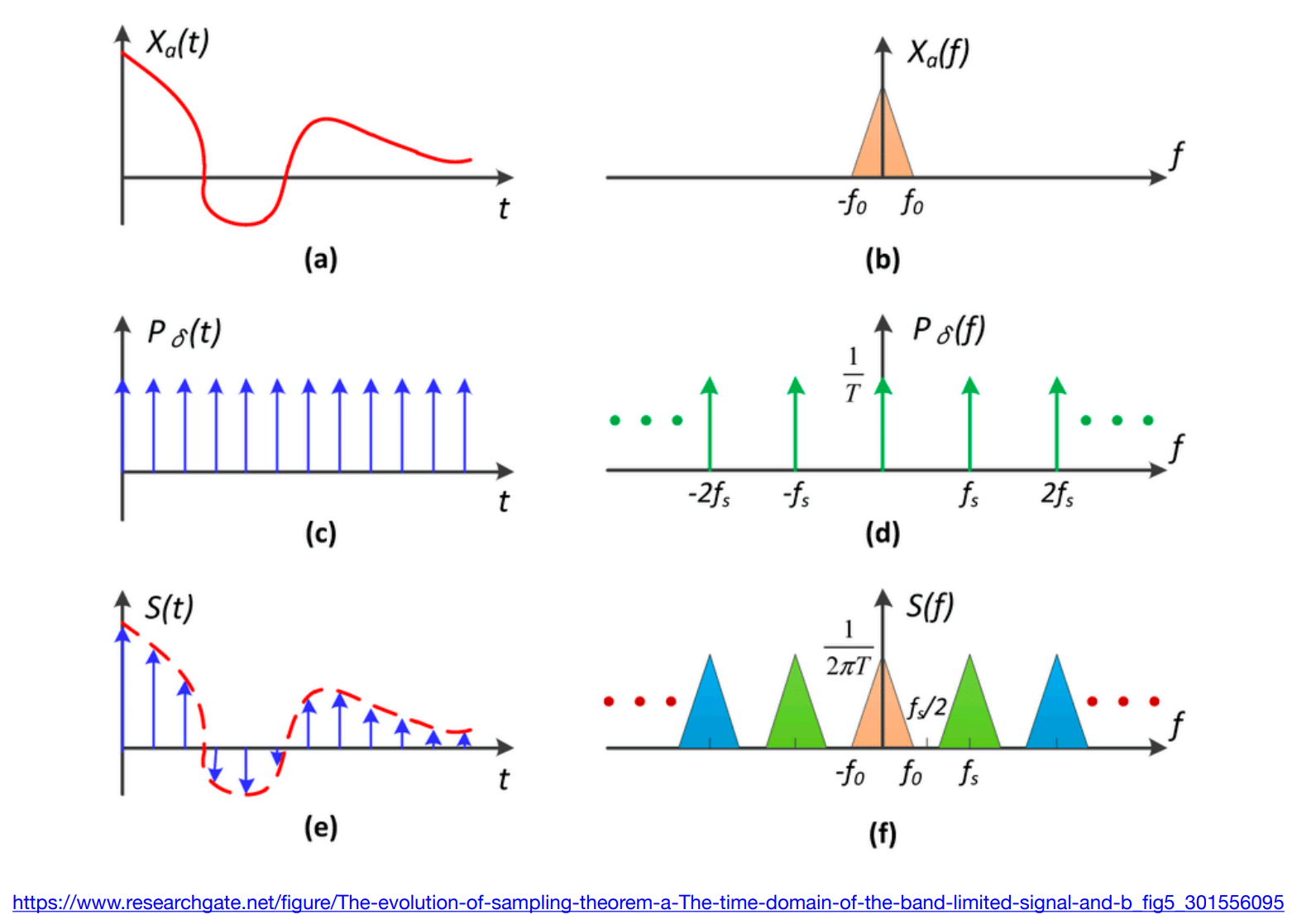
Sampling

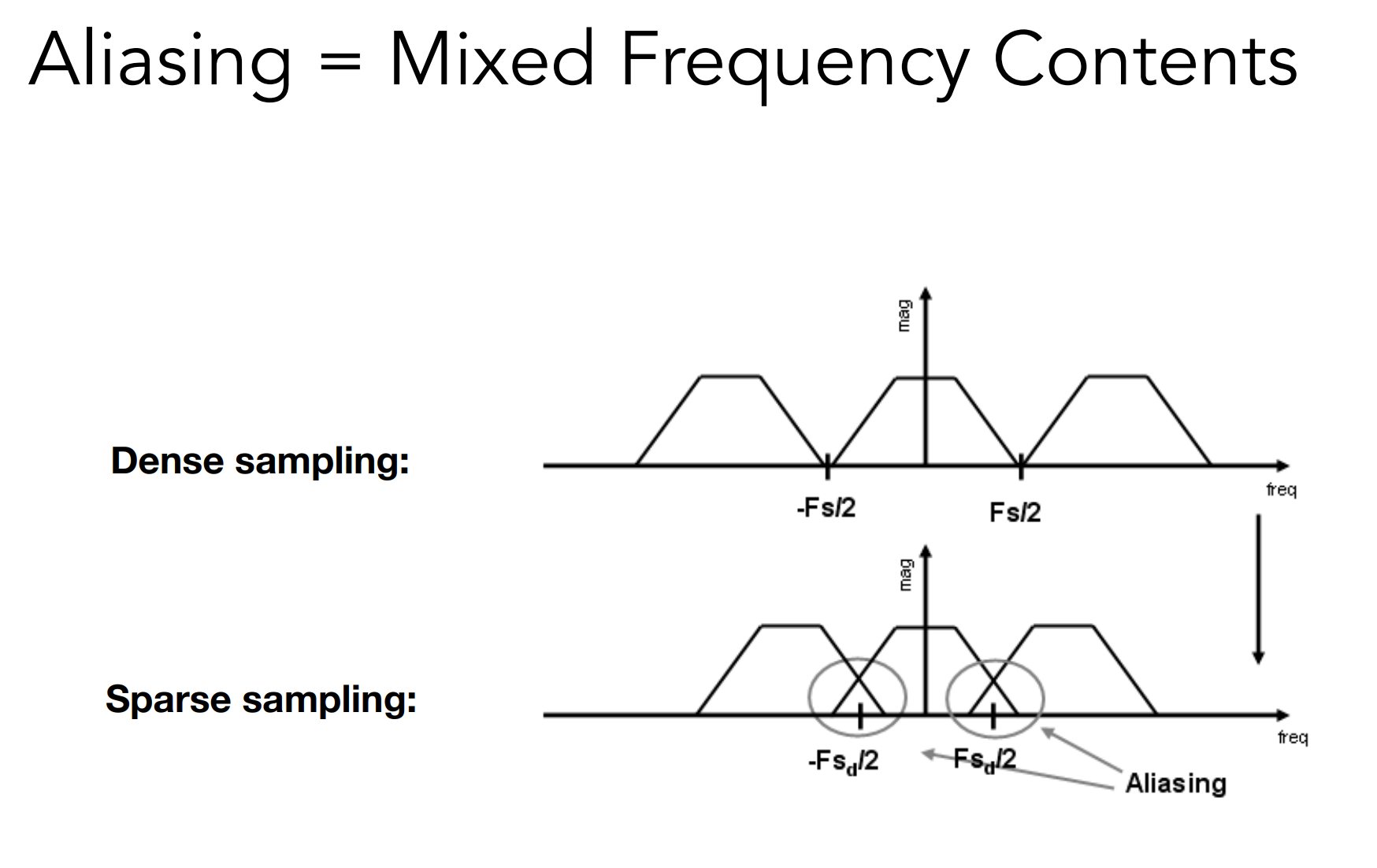
  • 锯齿=混叠MixedFrequencyContents

d). Antialiasing

  • 解决锯齿的选择：
    • 提高采样率
      • 增大冲激信号在频域的距离；
      • 更高分辨率的显示器；
      • 缺点：成本高，且需要很高的分辨率
    • 抗锯齿
      • 让信号在采样（重复，Repeat）前变“窄”，即在采样前过滤掉高频部分
  • Antialiasing = Limiting, then repeatingAA
  • Pre-Filter
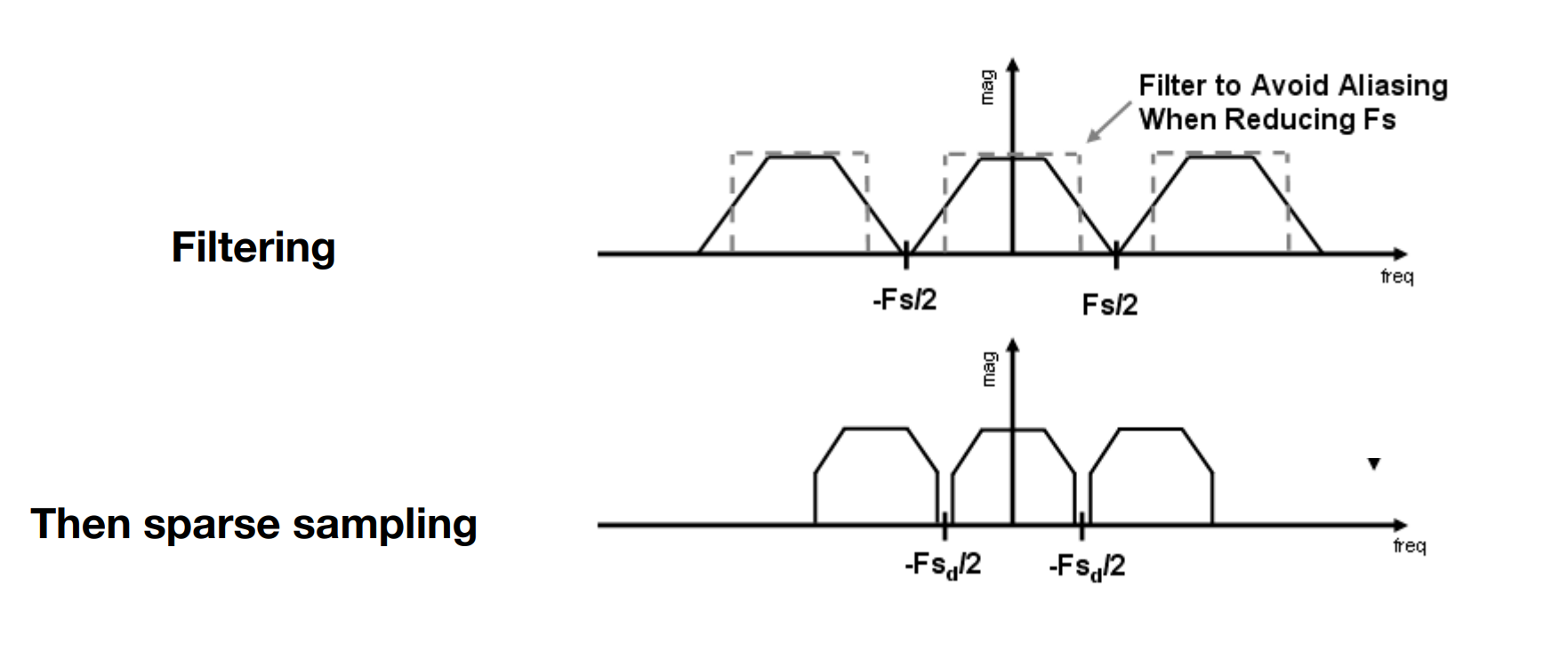
    • Solution:
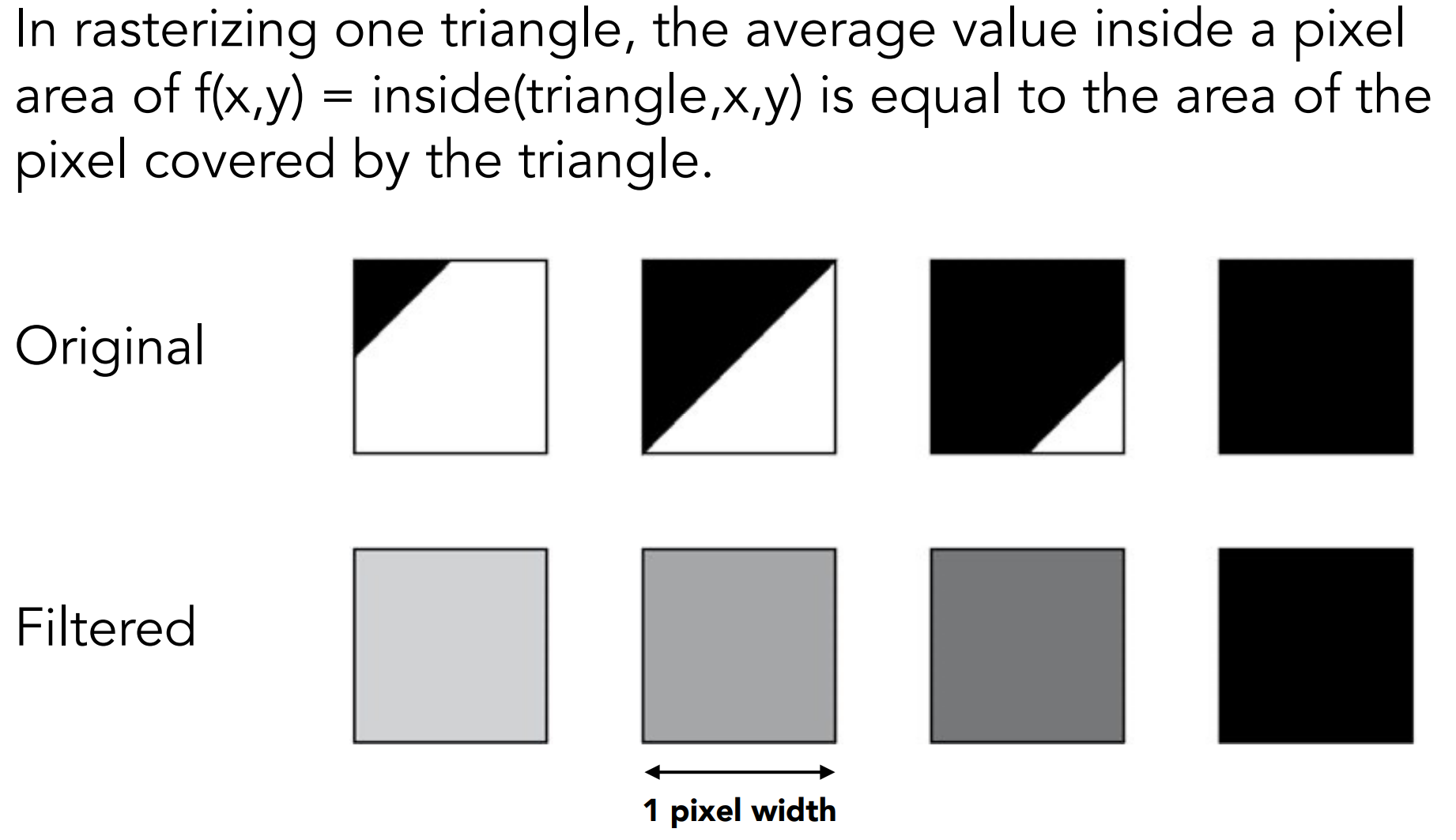
      • Convolve f(x,y) by a 1-pixel box-blur
        • Recall: convolving = filtering = averaging
      • Then sample at every pixel’s center
  • 通过计算像素平均值来抗锯齿Avertage_Pixel_Value

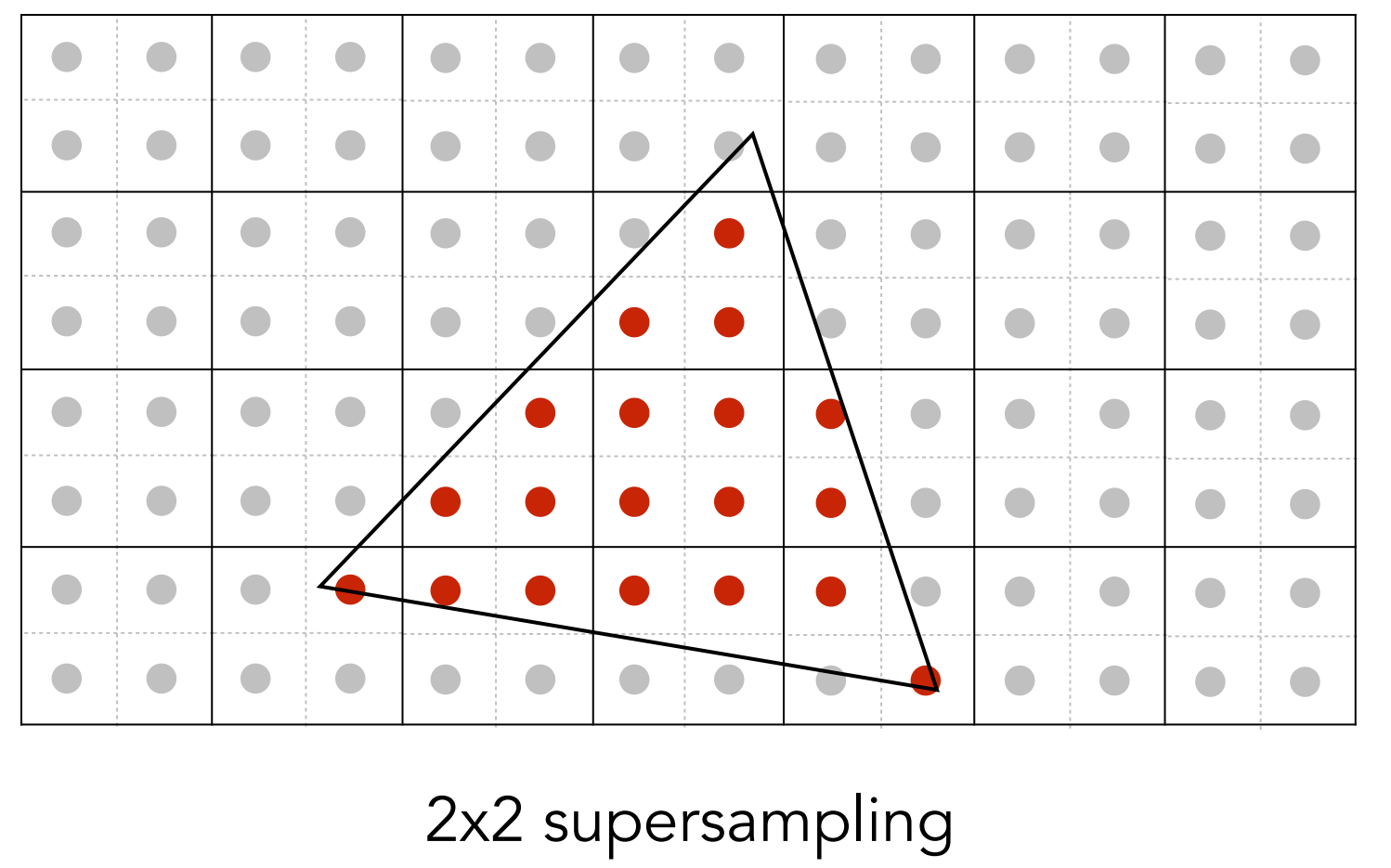
e). SSAA(Super Sampling Antialiasing)

  • 通过将一个像素分割成NxN个像素来进行采样和shading，最后将每个像素点内部所细分的采样点的颜色值全部加起来再求均值，作为该像素点的抗锯齿之后的颜色值SSAA

f). MSAA(Multi-Sampling Antialiasing)

  • MSAA是对SSAA的改进。SSAA的计算量大，一个像素中会有多个点进行shading，而MSAA只是计算究竟有几个采样点会被三角形cover，计算颜色的时候只会利用像素中心坐标进行一次shading。MSAA
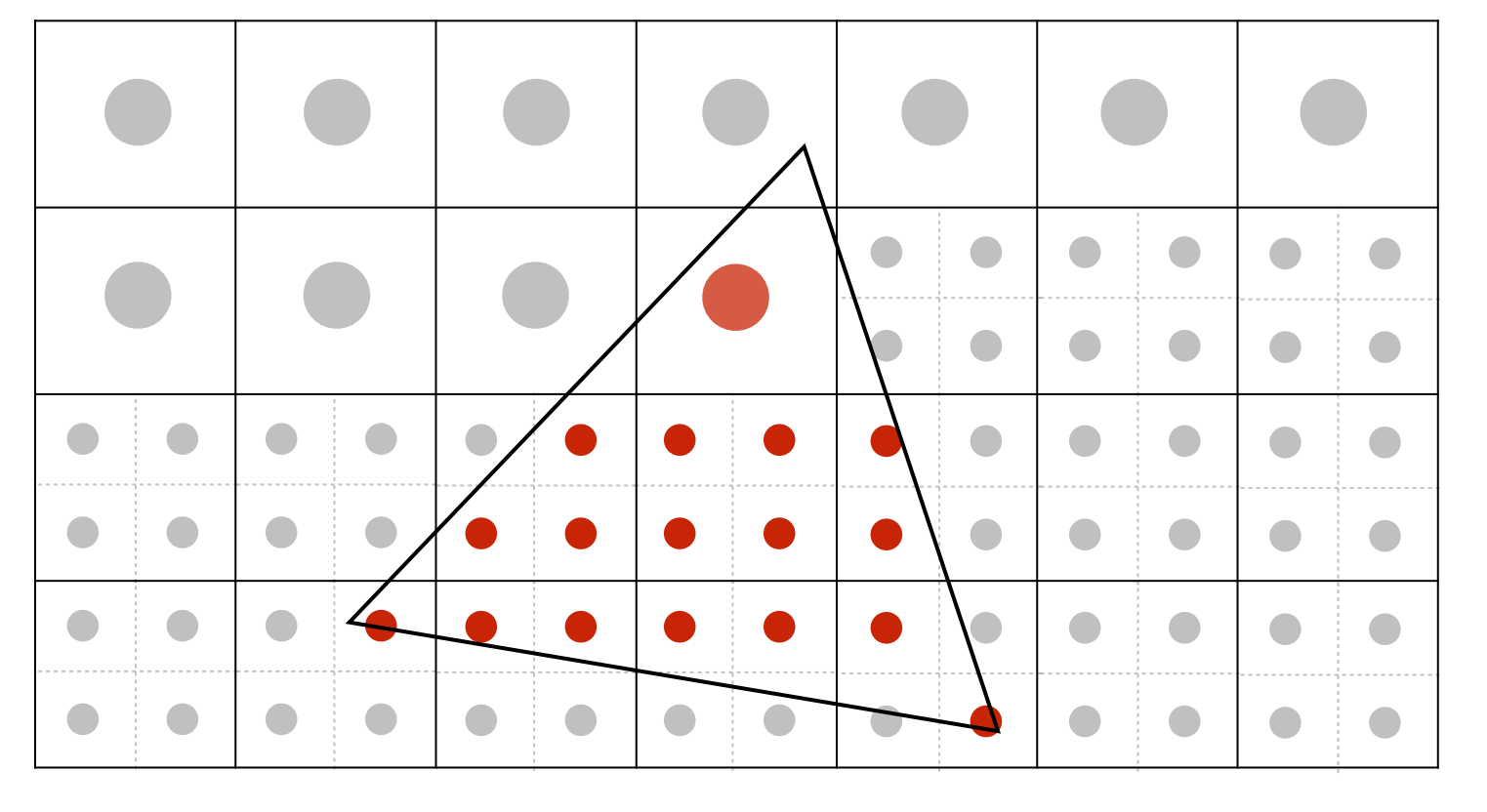
  • 如图中大点所在的像素块，三角形只覆盖了其中的三个点（左下，右上，右下），则该像素的颜色为$75\%Color_{origin}$，之后，再对像素中心进行采样
  • 注意：MSAA只是近似Blur，而没提高采样率。要注意和SSAA以及高分辨率的区分
  • 在实际中，子像素的划分并不是均匀划分为NxN，而是通过其他更有效的方法，而且有些样本还会得到复用；
  • SSAA中每个像素点有4个子采样点，每个三角形对每个像素点的4个子采样点各着色1次（共4次），再把计算结果根据深度和覆盖信息保存到对应的子采样点，最后对4个采样点取均值作为最终的像素颜色；
  • MSAA中每个像素点有4个子采样点，每个三角形对每个像素点只在中心点着色1次，再把计算结果根据深度和覆盖信息保存到对应的子采样点，最后对4个采样点取均值作为最终的像素颜色；

g). Other AA

  • FXAA(Fast Approximate AA)
    • 图像层面上进行处理，是一个后期处理，先得到有锯齿的图像，再通过图像匹配找到有锯齿的边界，之后，替换为没有锯齿的边界；
  • TAA(Temporal AA)
    • 可以联系UE_NOTE
    • 将空域采样点，均匀分布到时域上；

h). Z-buffer

h.0). Painter’s Algorithm

  • 画家算法：
    • 对三角形进行排序，先画远的，再画近的；
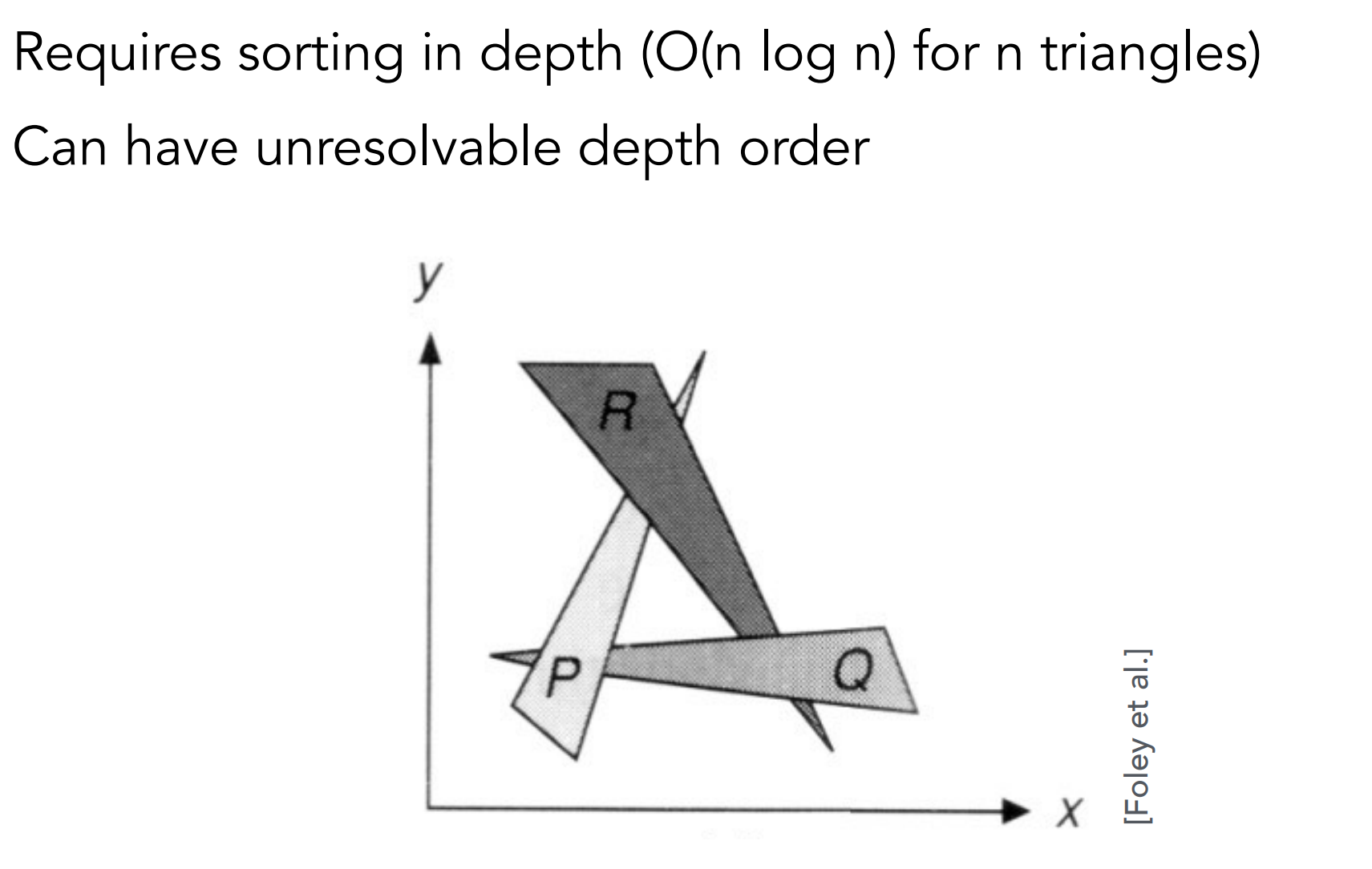
    • 不能解决相互遮挡问题，因此采用Z-bufferPainters_Algorithm

h.1). Z-buffer

  • Idea：
    • 储存每个采样（像素）中最小的深度值；
    • 储存深度值到缓存区（buffer）中；
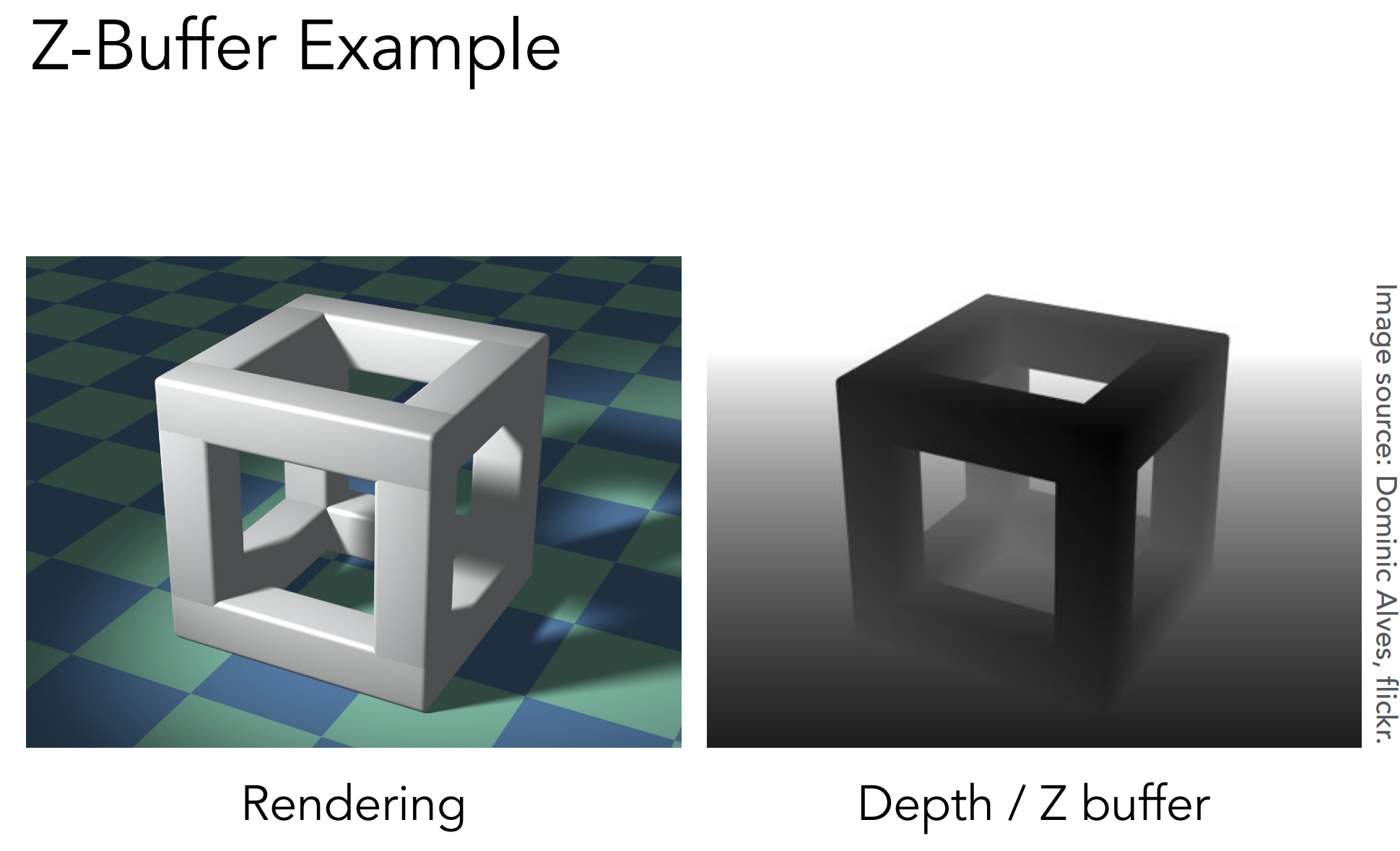
  • 为了简单起见，我们看作z是正数(smaller z -> closer, larger z -> further)；Z-Buffer
  • 深度缓存步骤：
    1. 初始化深度缓存，将其中每个值初始化为∞
    2. 遍历每个三角形面上的每一个像素点[x,y]，如果该像素点的深度值z，小于Z-buffer[x,y]中的值，则更新zbuffer[x,y]值为该点深度值z，并同时更新该像素点[x,y]的颜色为该三角形面上的该点的颜色。
      • 伪代码：PCode

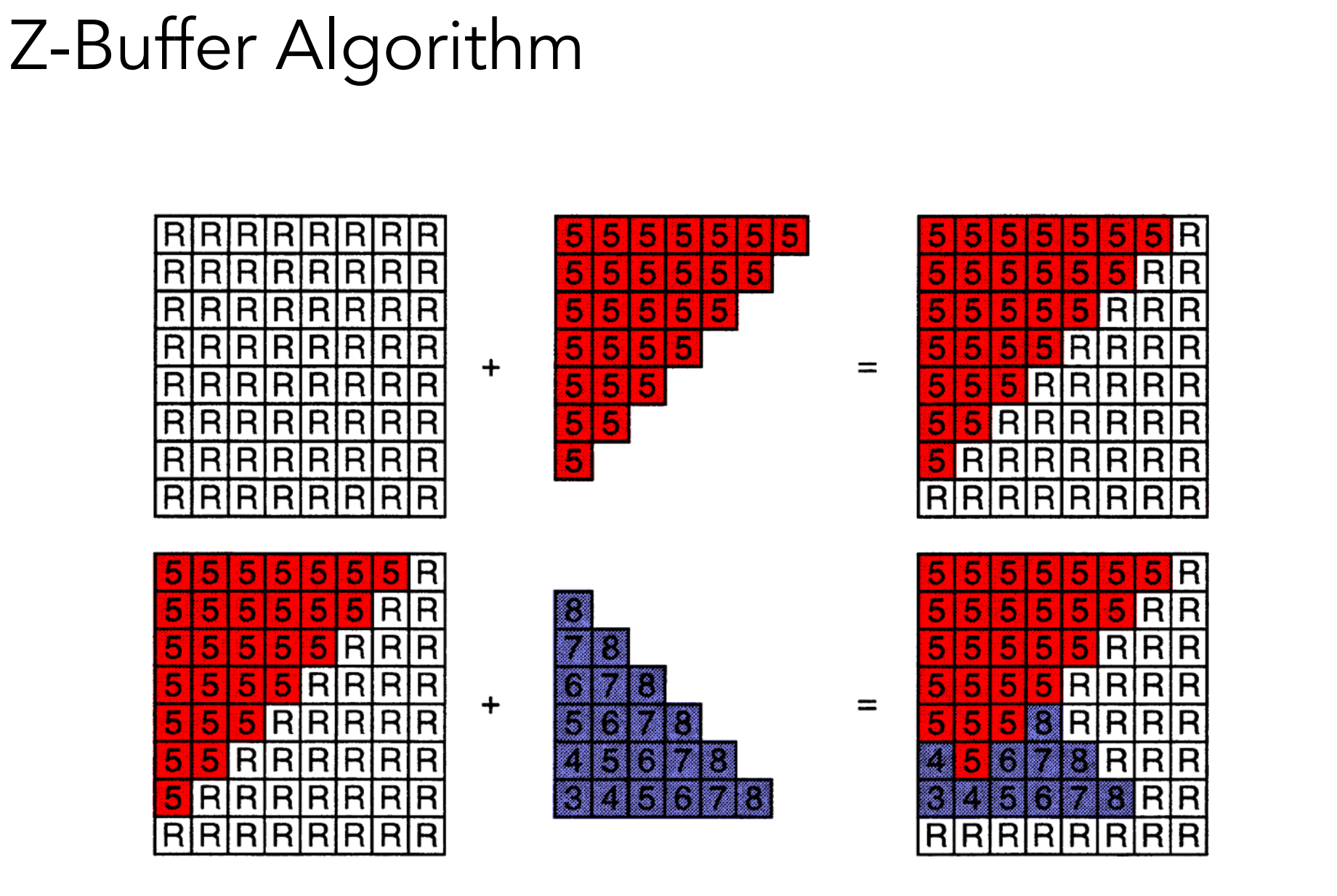
Z-Buffer_Algorithm

  • 时间复杂度$O(n)$。Z-buffer并没有进行排序，只是求得最小（深度）值，因此时间复杂度为线性；
  • 三角形的绘制顺序并不影响最终结果（不考虑不透明等情况）；