Games101-7-9 Shading
Lecture 07/08 Shading(Illumination, Shading and Graphics Pipeline)
a). Definition

b). A Simple Shading Model(Blinn-Phong Reflectance Model)
b.1). Fundamental
Blinn-Phong是一个经验模型,并不是严格基于物理的;
进入视线内的光照一般有以下构成:
- 高光(Specualr)
- 漫反射(Diffuse)
- 环境光(Ambient)
- 自发光(Emissive)
Shading is Local: Compute light reflected toward camera at a specific shading point
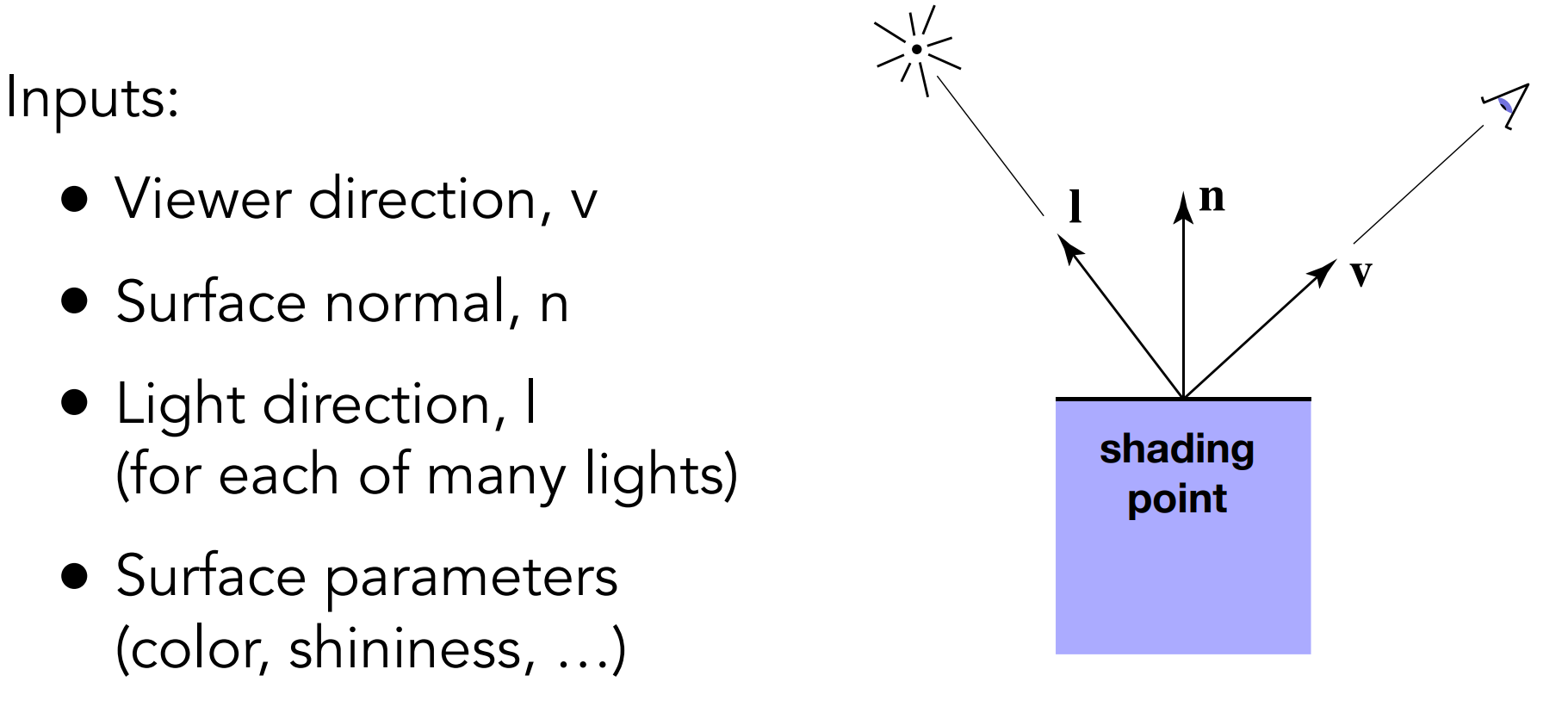
No shadows will be generated! (shading ≠ shadow)
- 阴影会由另外的Shadow Caster来着色;

b.2). Diffuse Reflection
- Blinn-Phong中,漫反射的光均匀散射到各个方向;
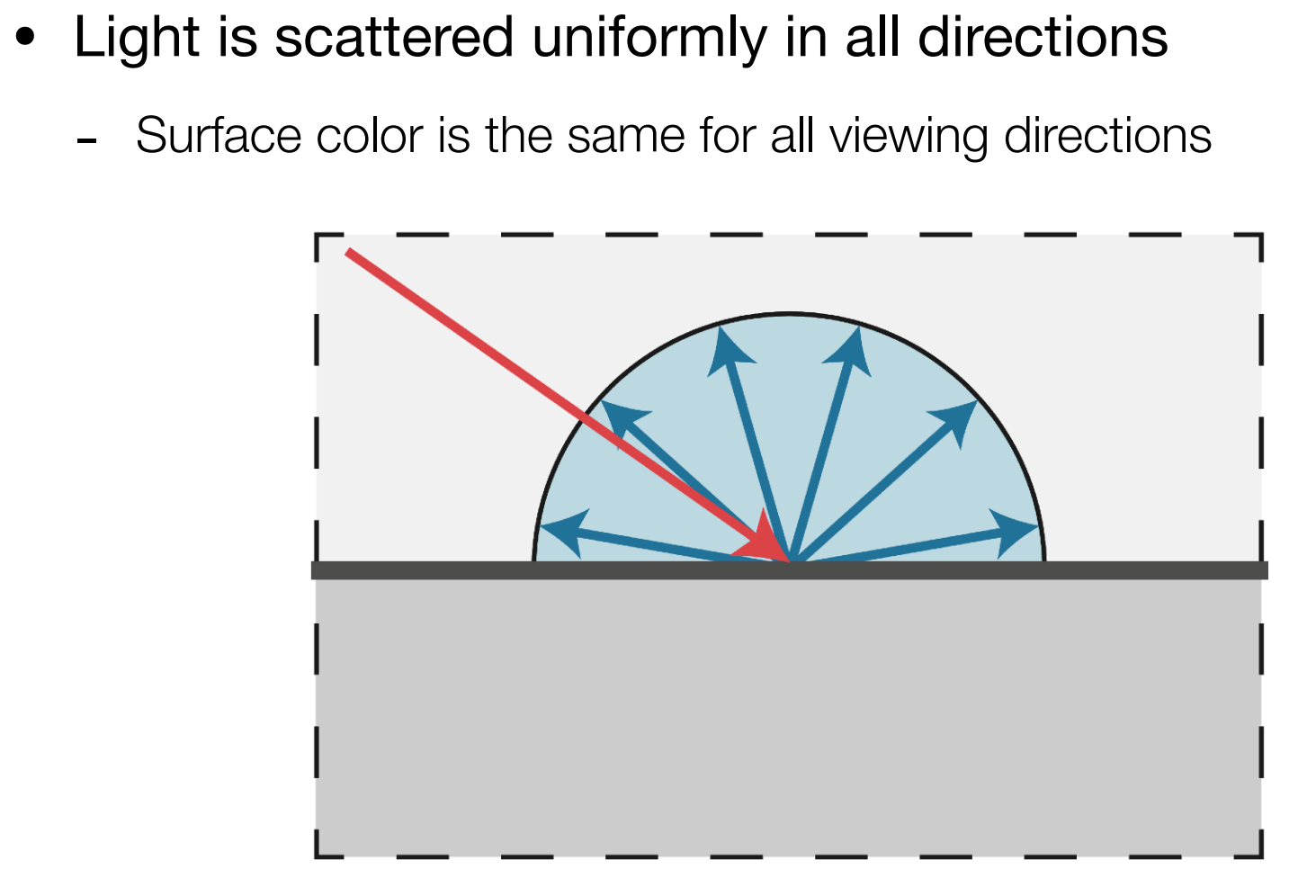
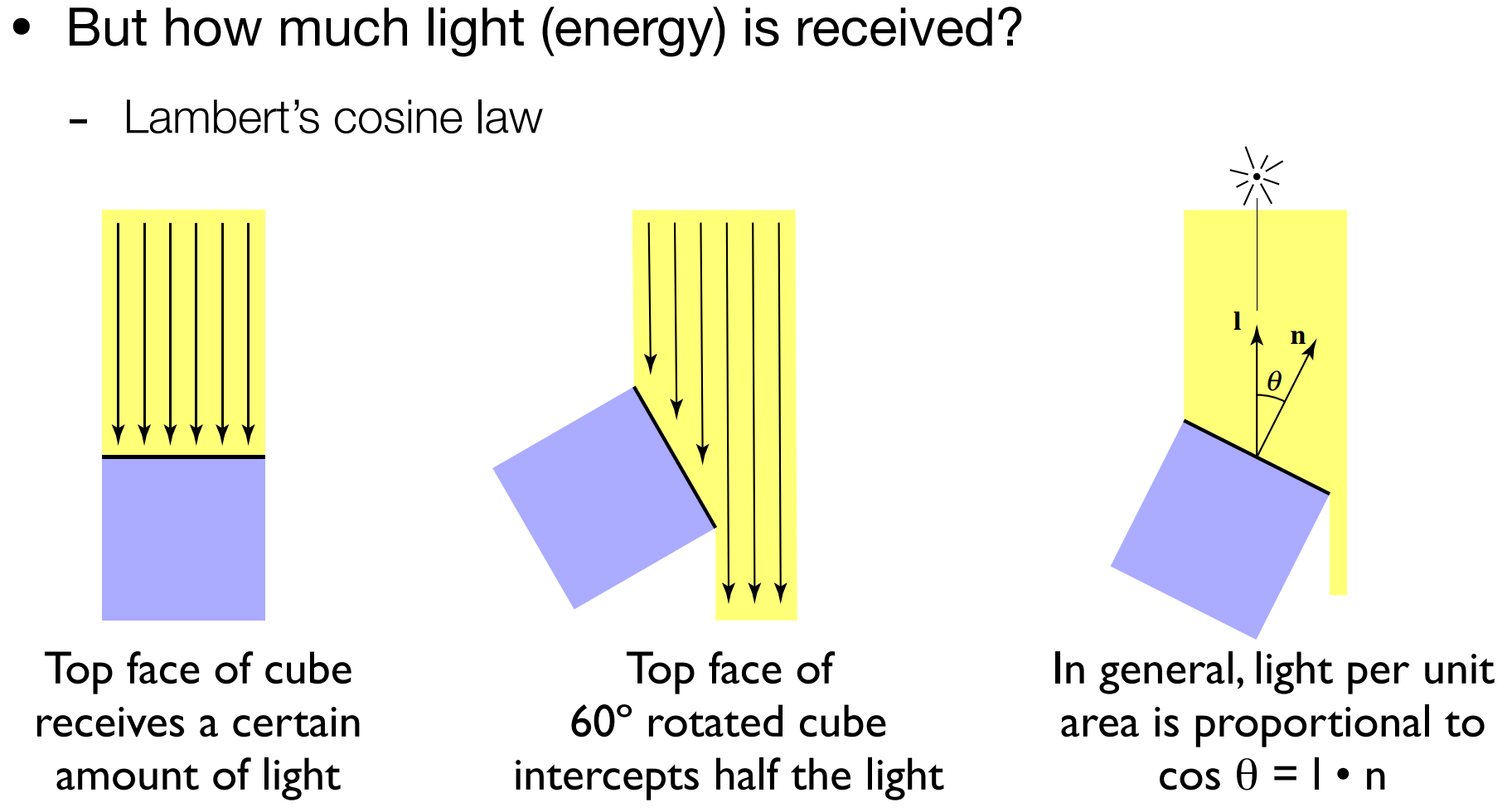
Lambert’s cosine law:接收到的能量与 $l·n$ 成正比例
Light Falloff
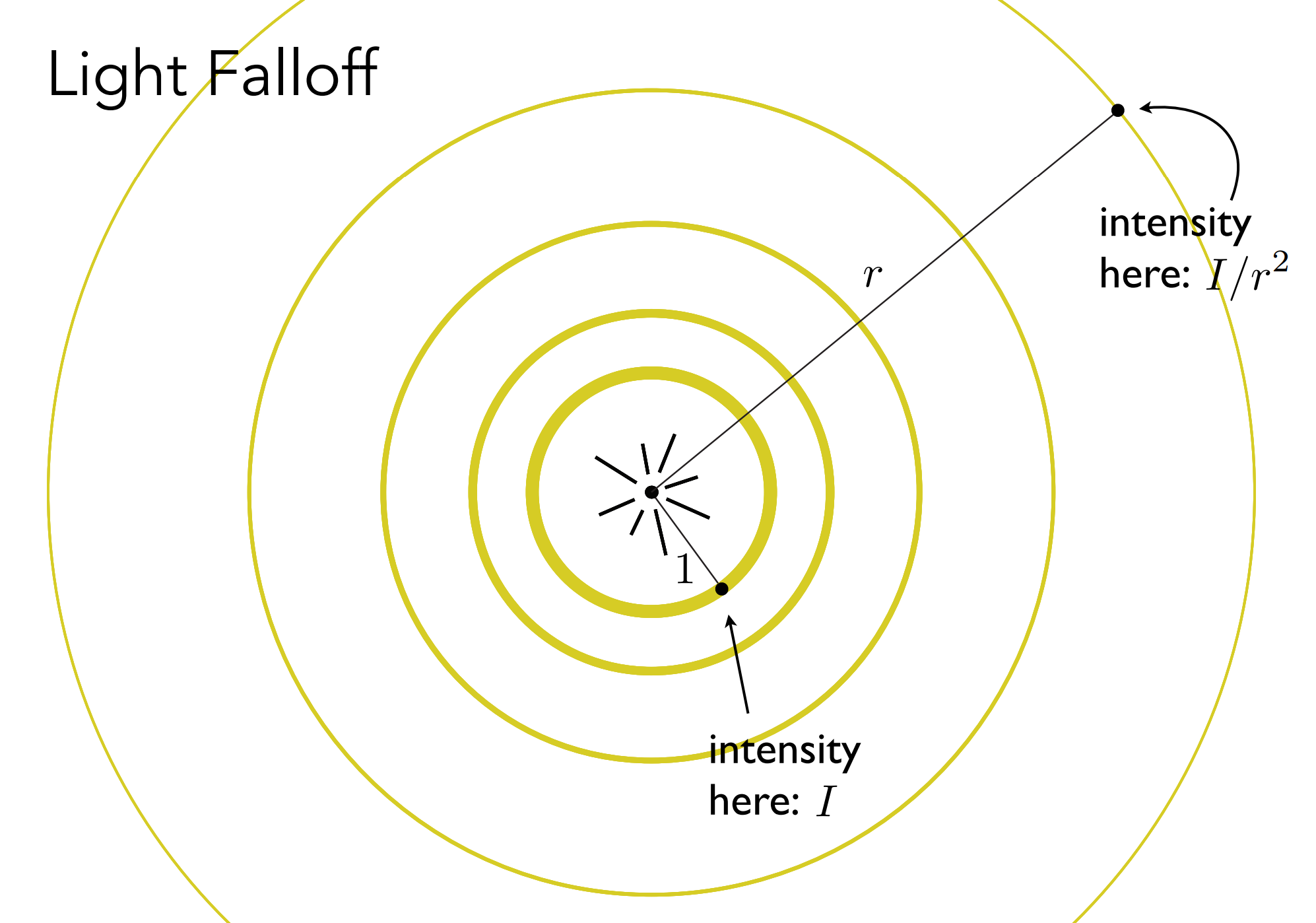
漫反射最终的着色:
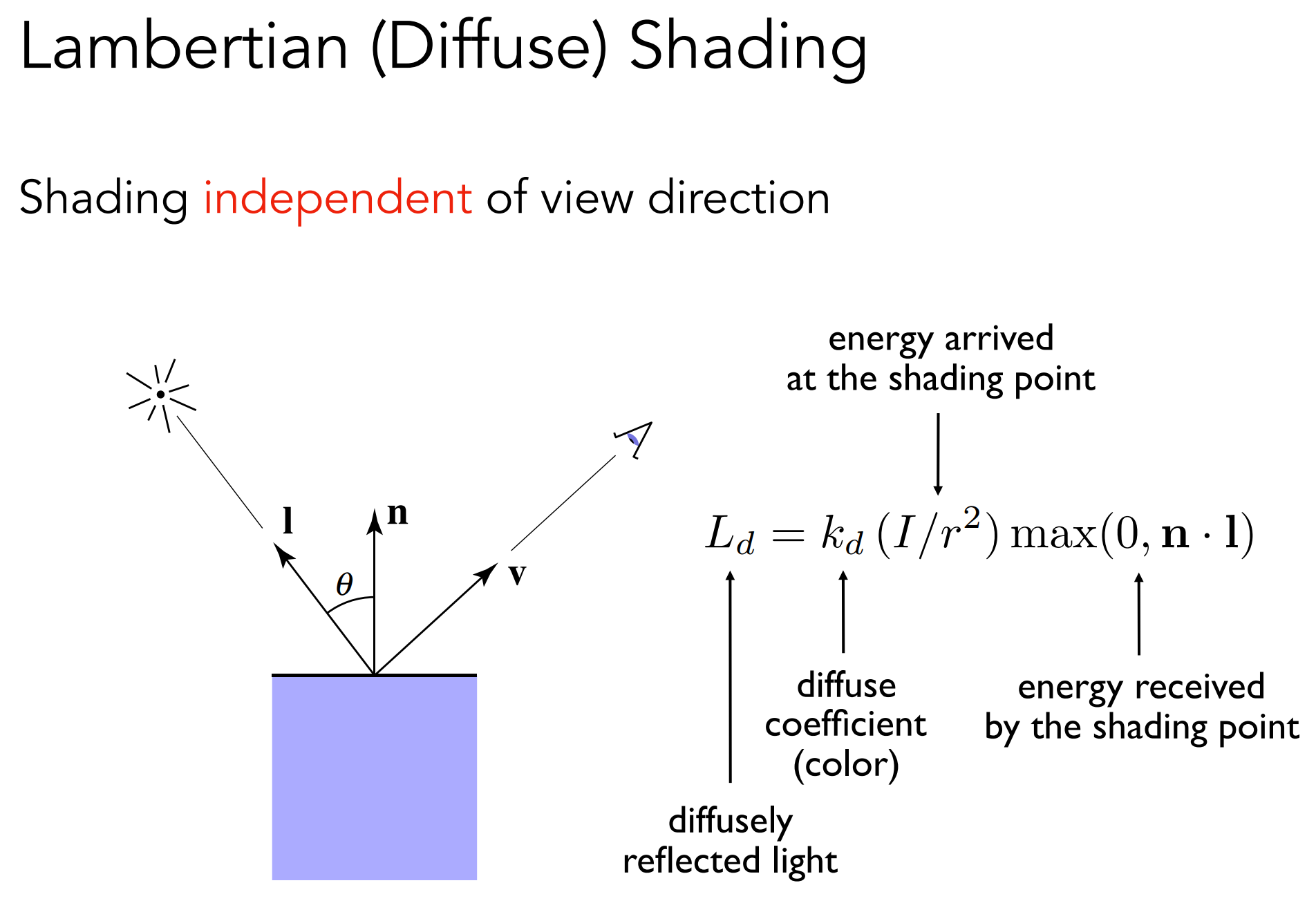

b.3). Specular Term(Blinn-Phong)
Intensity depends on view direction
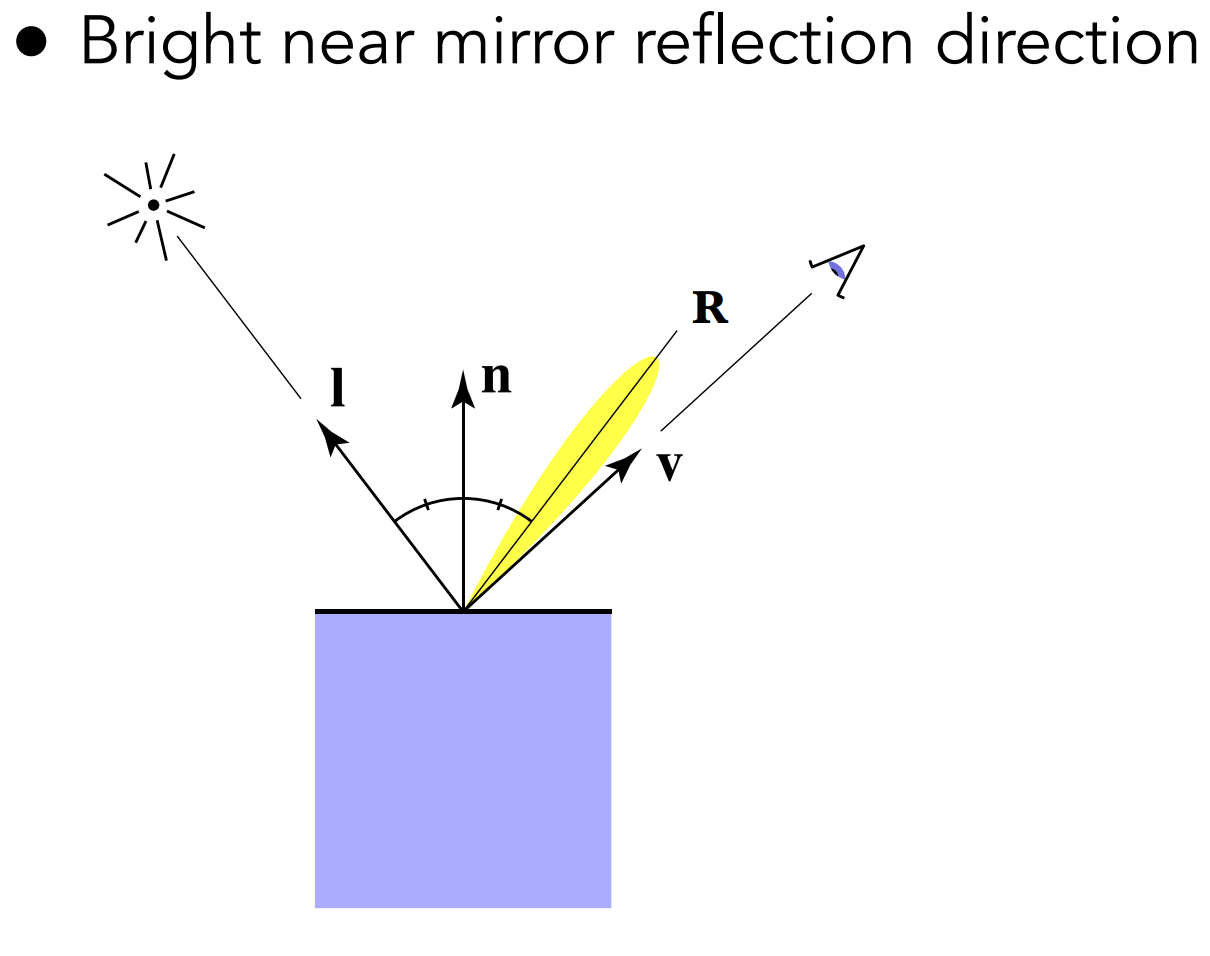
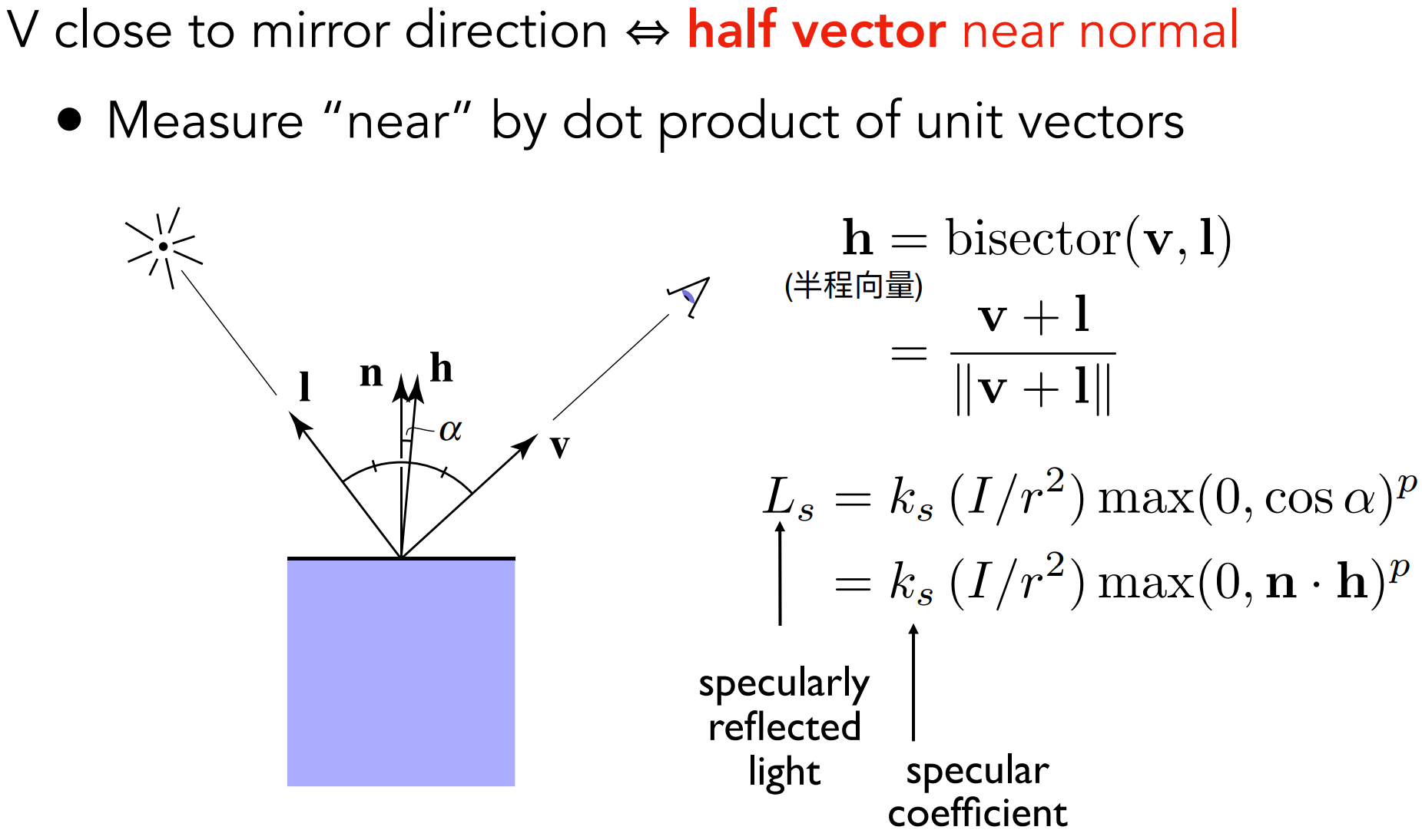
- 采用半程向量简化计算。采用半程向量$h$与$n$点乘的是Blinn-Phong模型,而采用镜面反射方向$r$和视线方向$v$点乘的是Phong模型;
- 指数$p$的作用:Increasing p narrows the reflection lobe
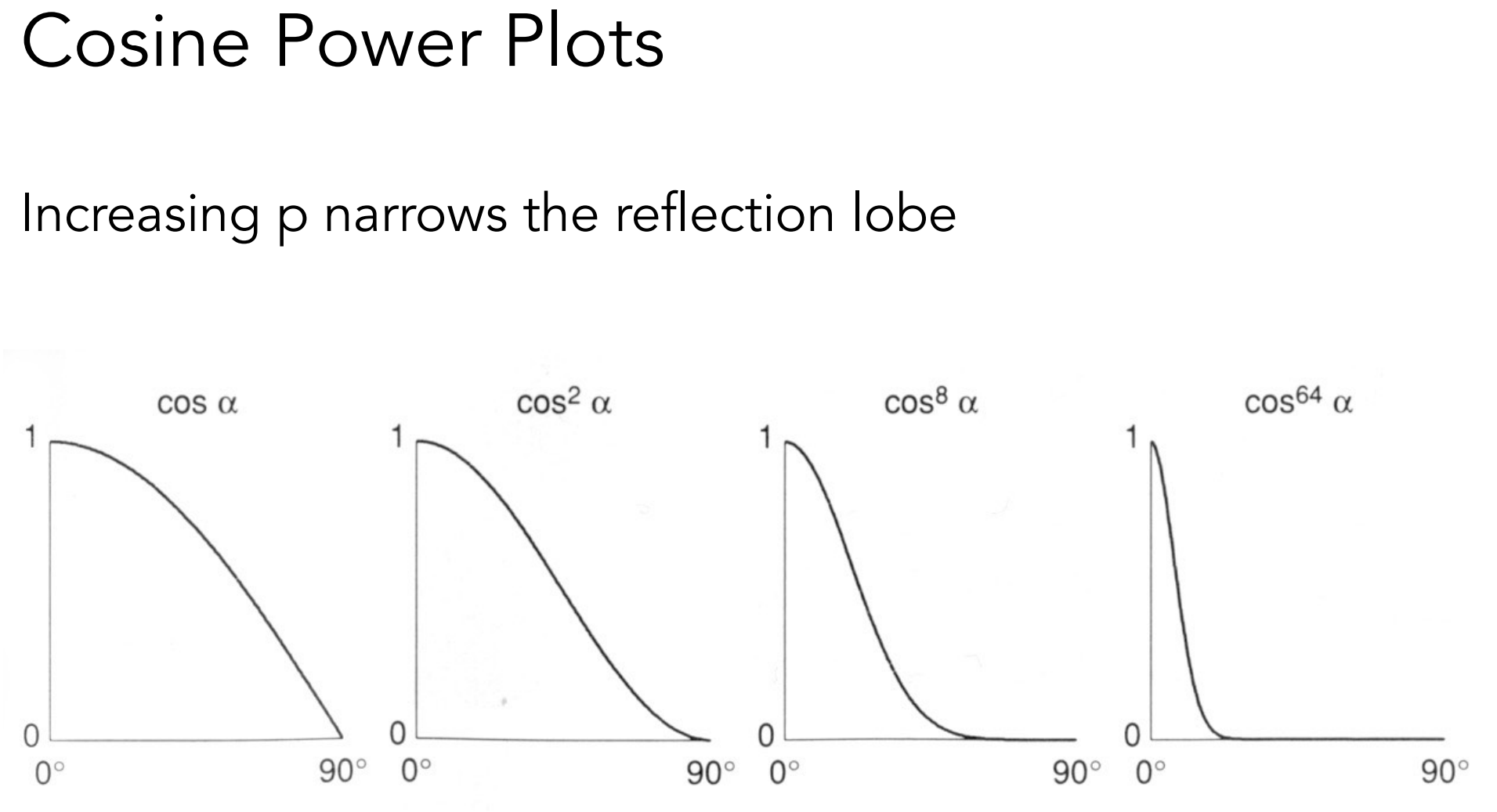
- 效果总览:
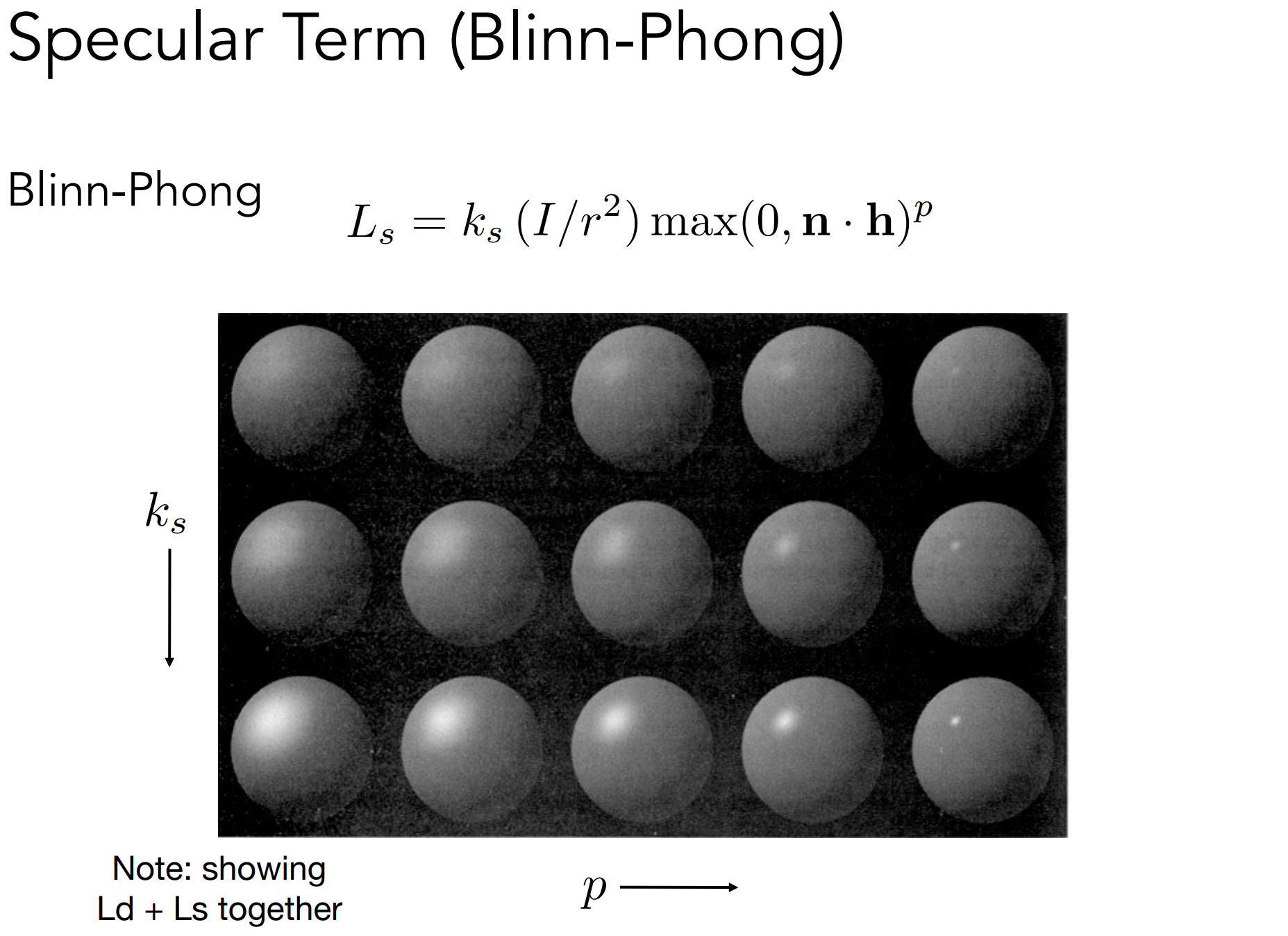
b.4). Ambient Term
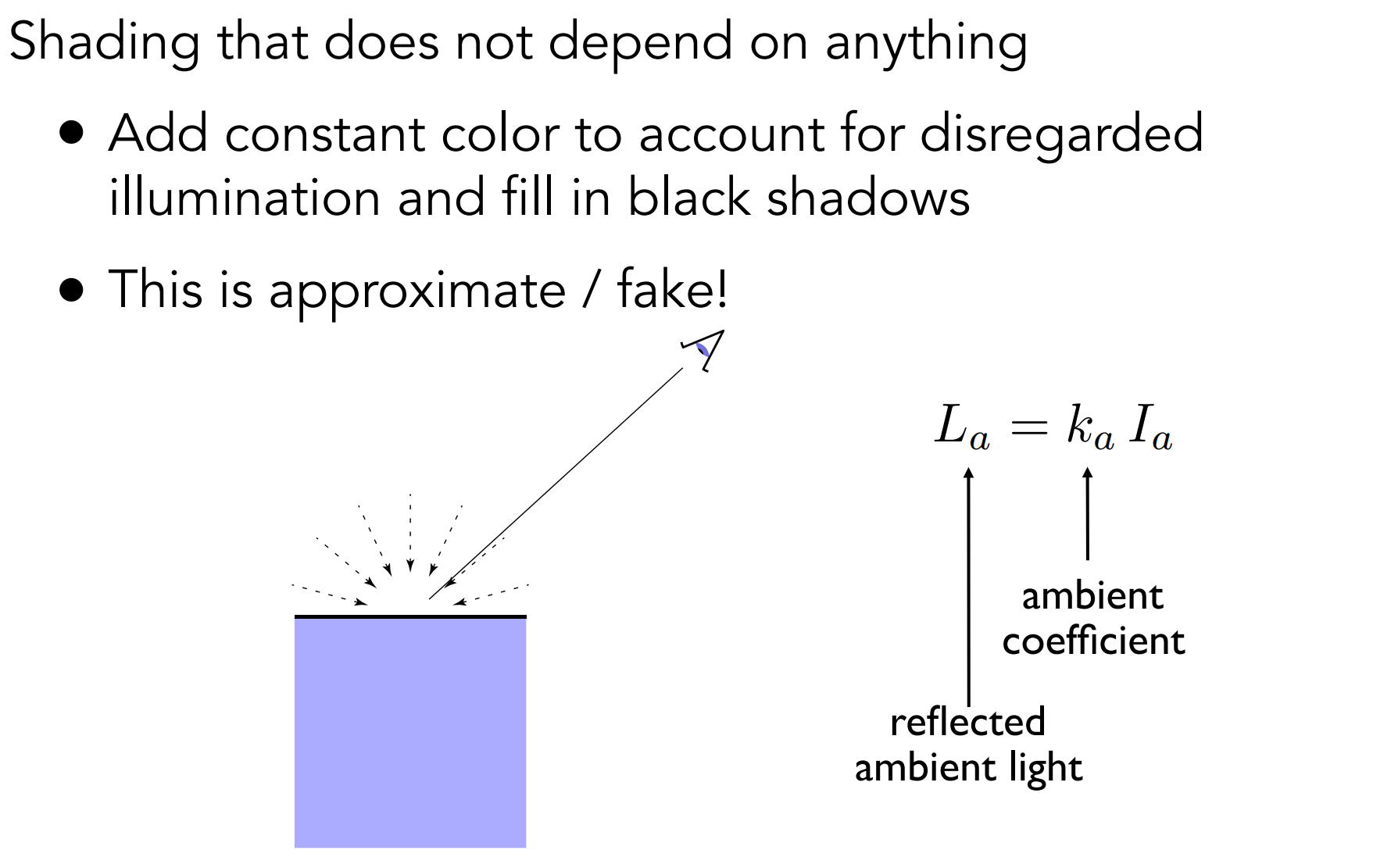

c). Shading Frequencies
c.1). Flat shading
c.2). Gouraud shading 
c.3). Phong shading
c.4). 对比
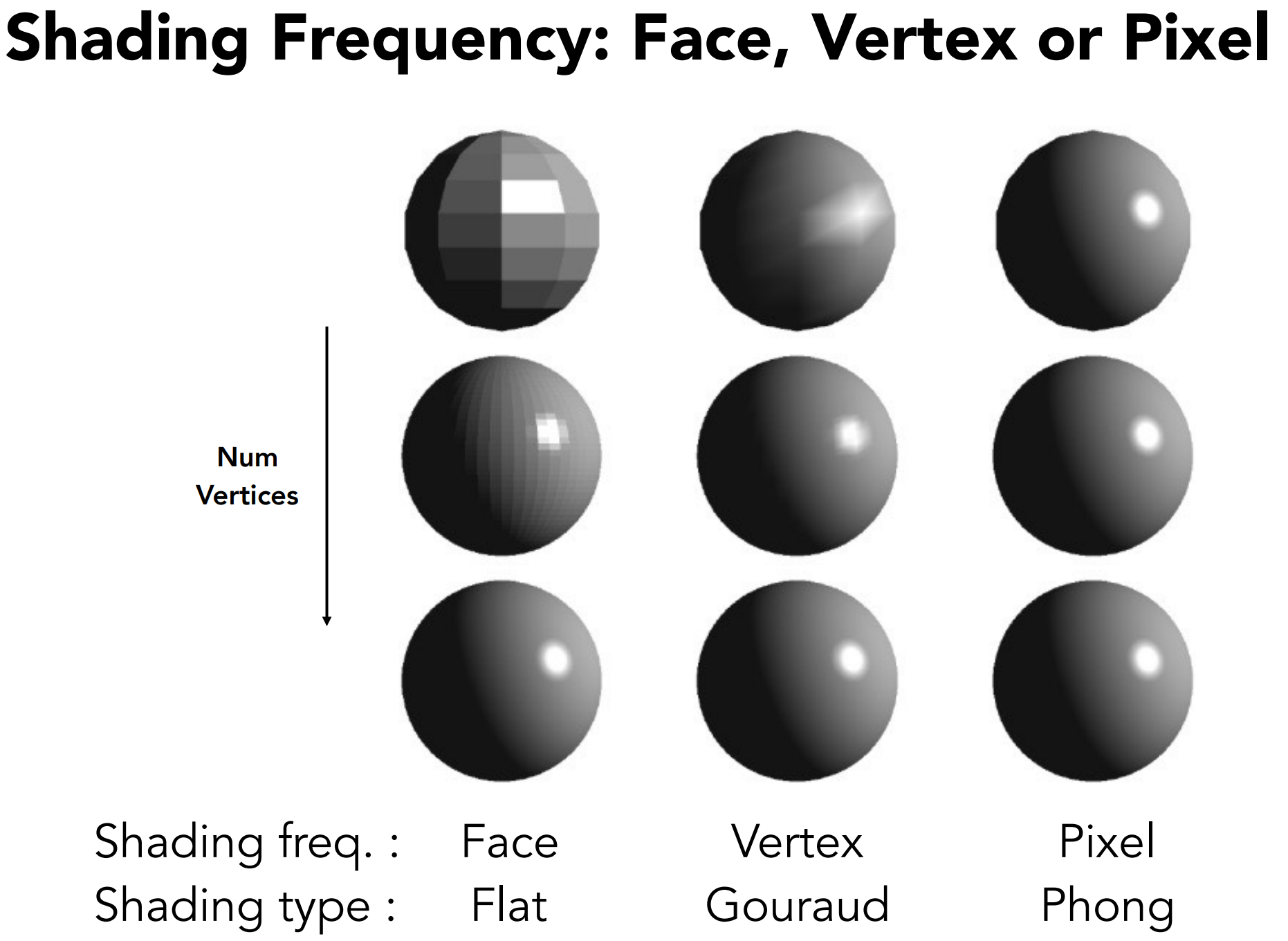
- 不一定Phong着色就比Flat优秀。在极高面数的一些情况下,Flat Shading性能开销比Phong Shading小,且呈现效果相差无几;
c.5). 定义顶点/像素法线
顶点法线为相邻三角形的加权平均(权重与三角面的面积有关,当然也可简单平均,但效果较加权平均差);
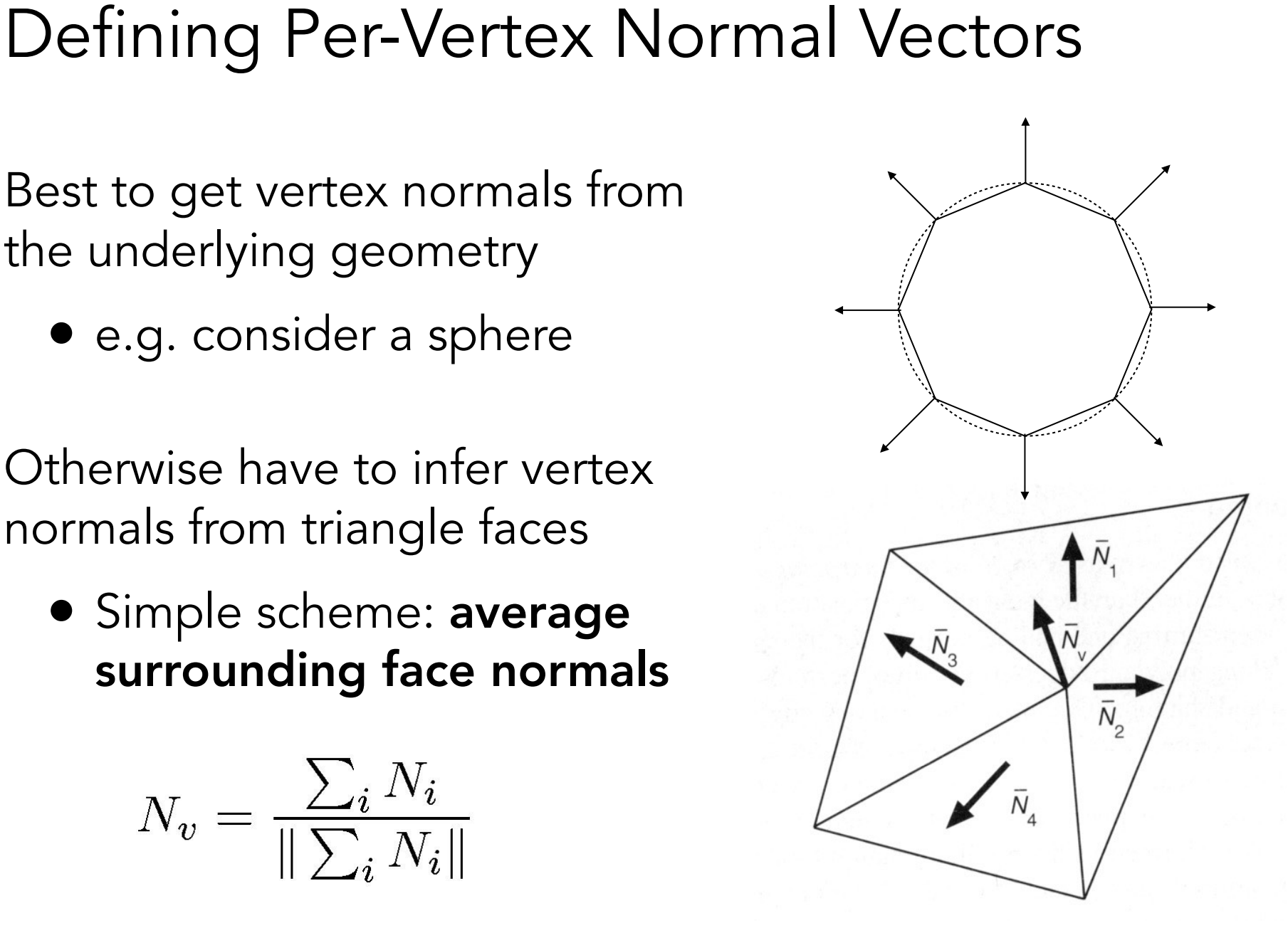
逐像素的法线通过对顶点法线进行重心插值(Barycentric interpolation)后归一化(normalize)得到;
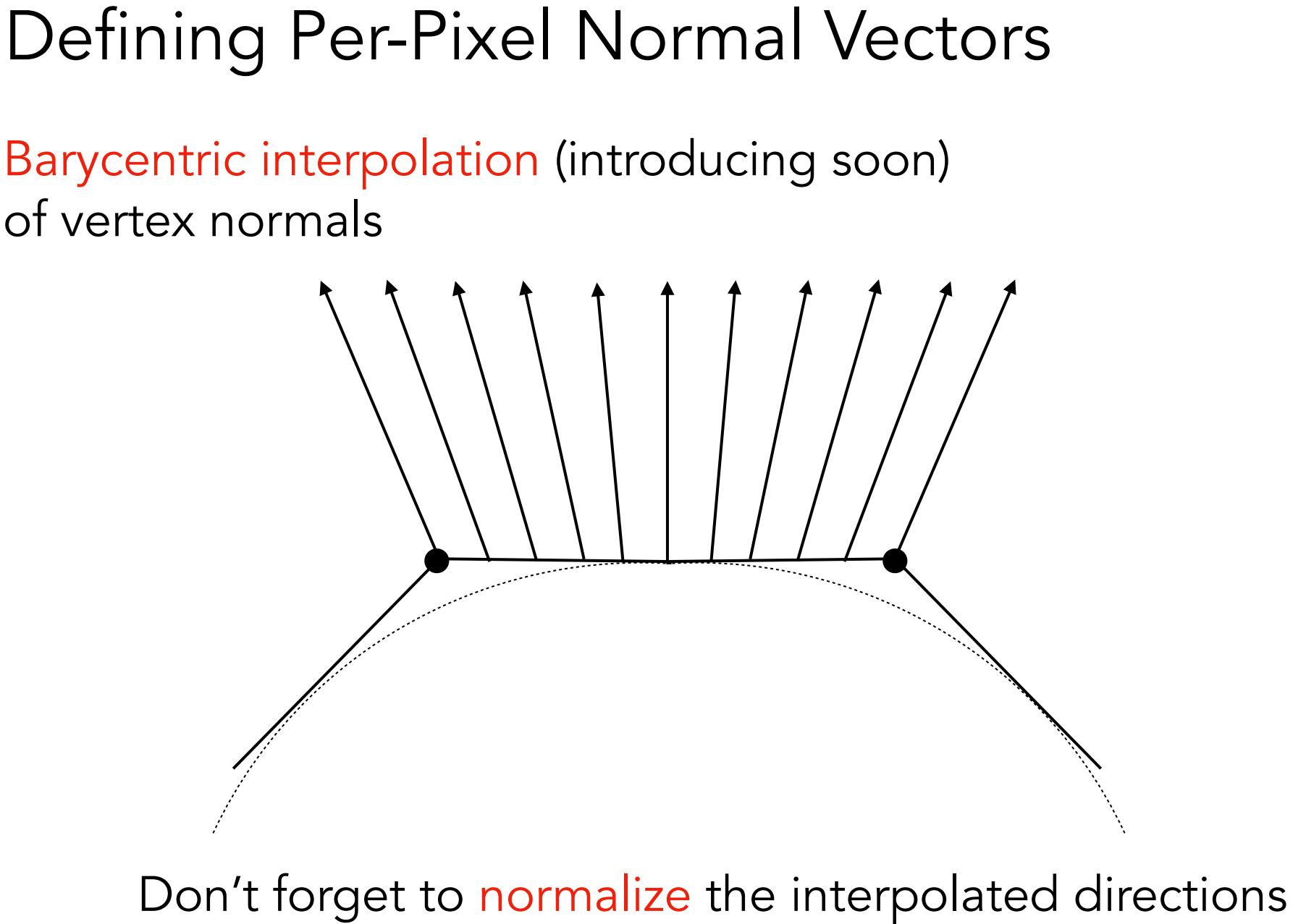
d). Graphics(Real-time Rendering) Pipeline
- 这段可看冯的入门精要作为简单的补充
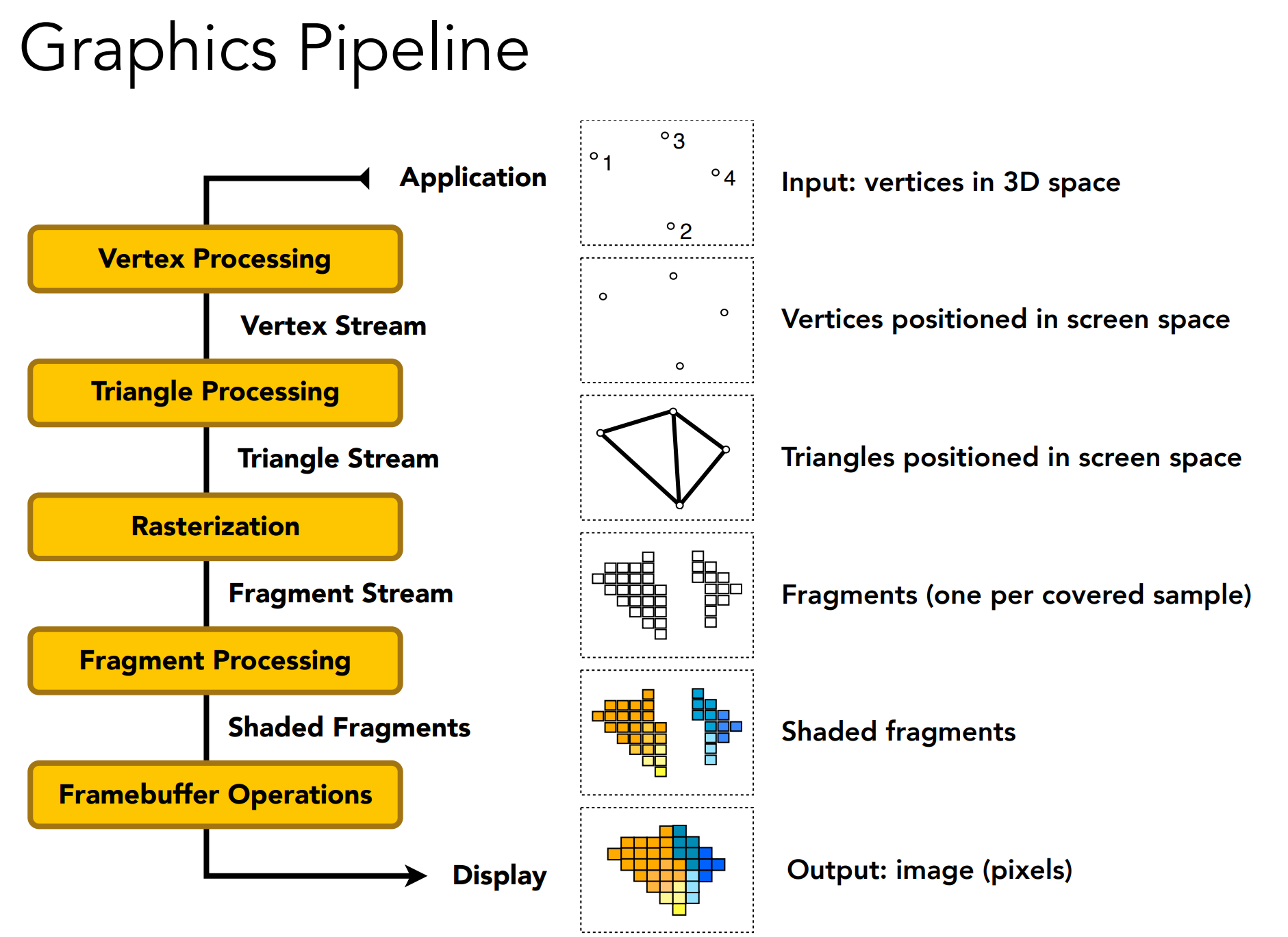
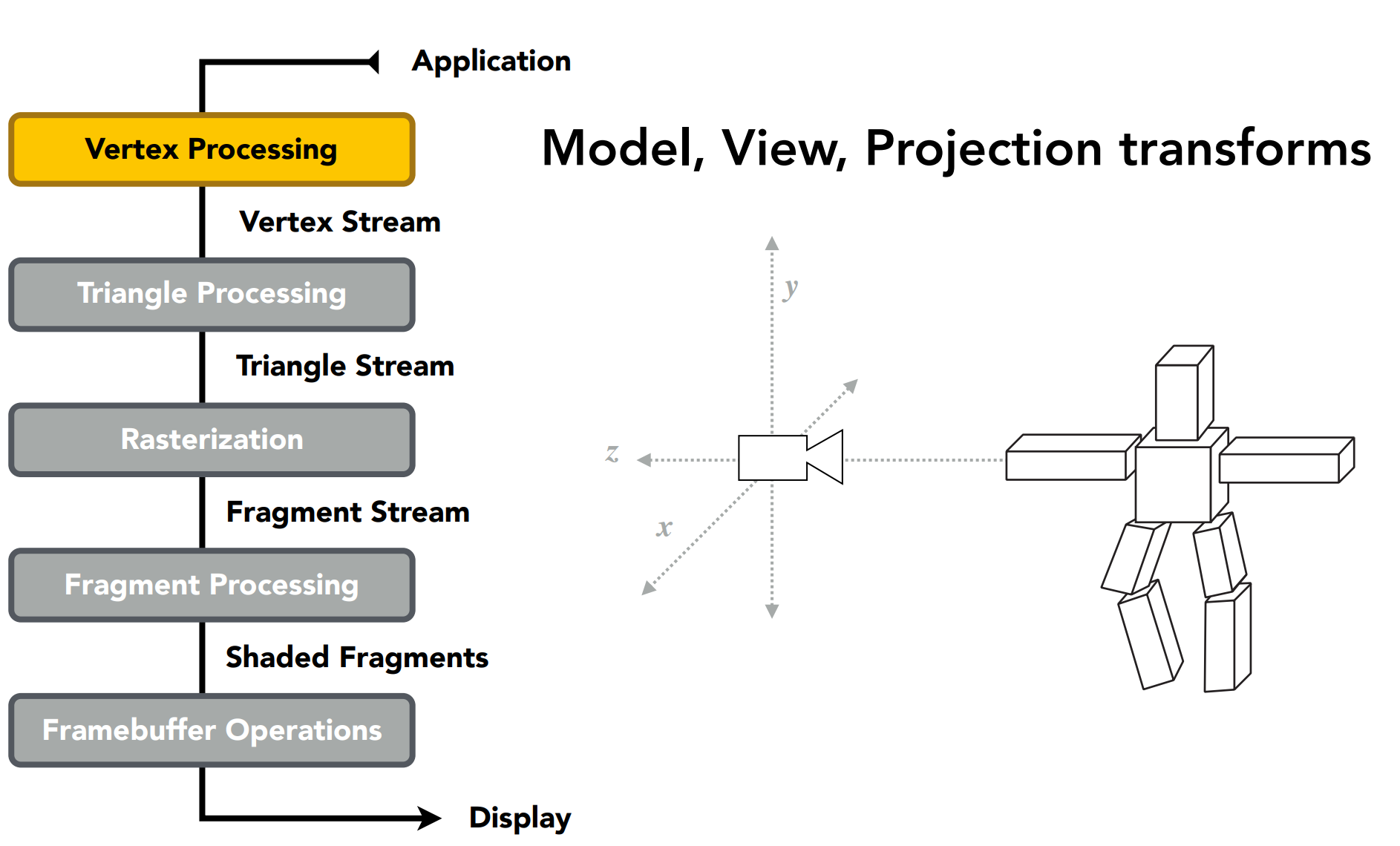
MVP矩阵相关的发生在顶点阶段;
光栅化;
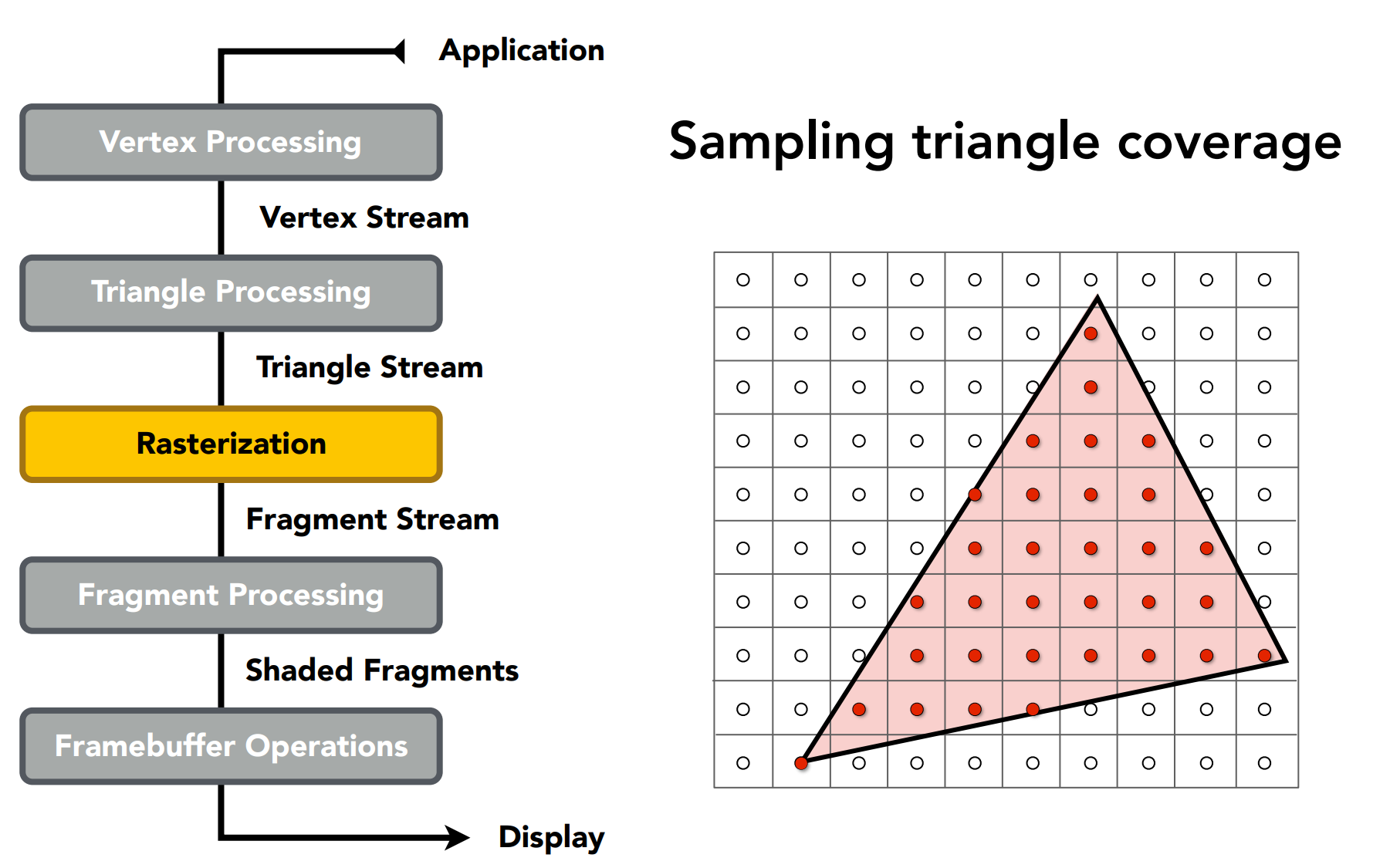
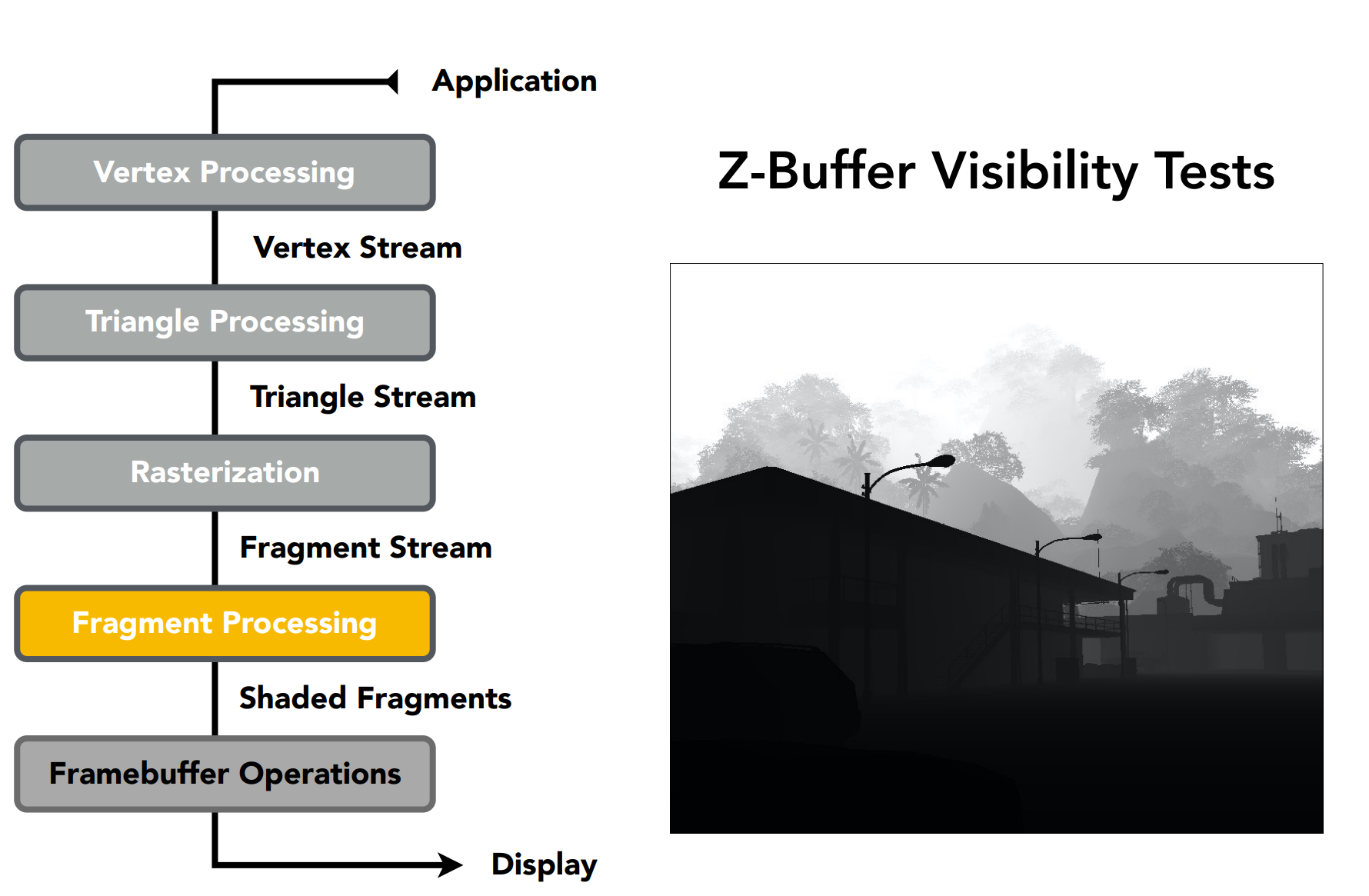
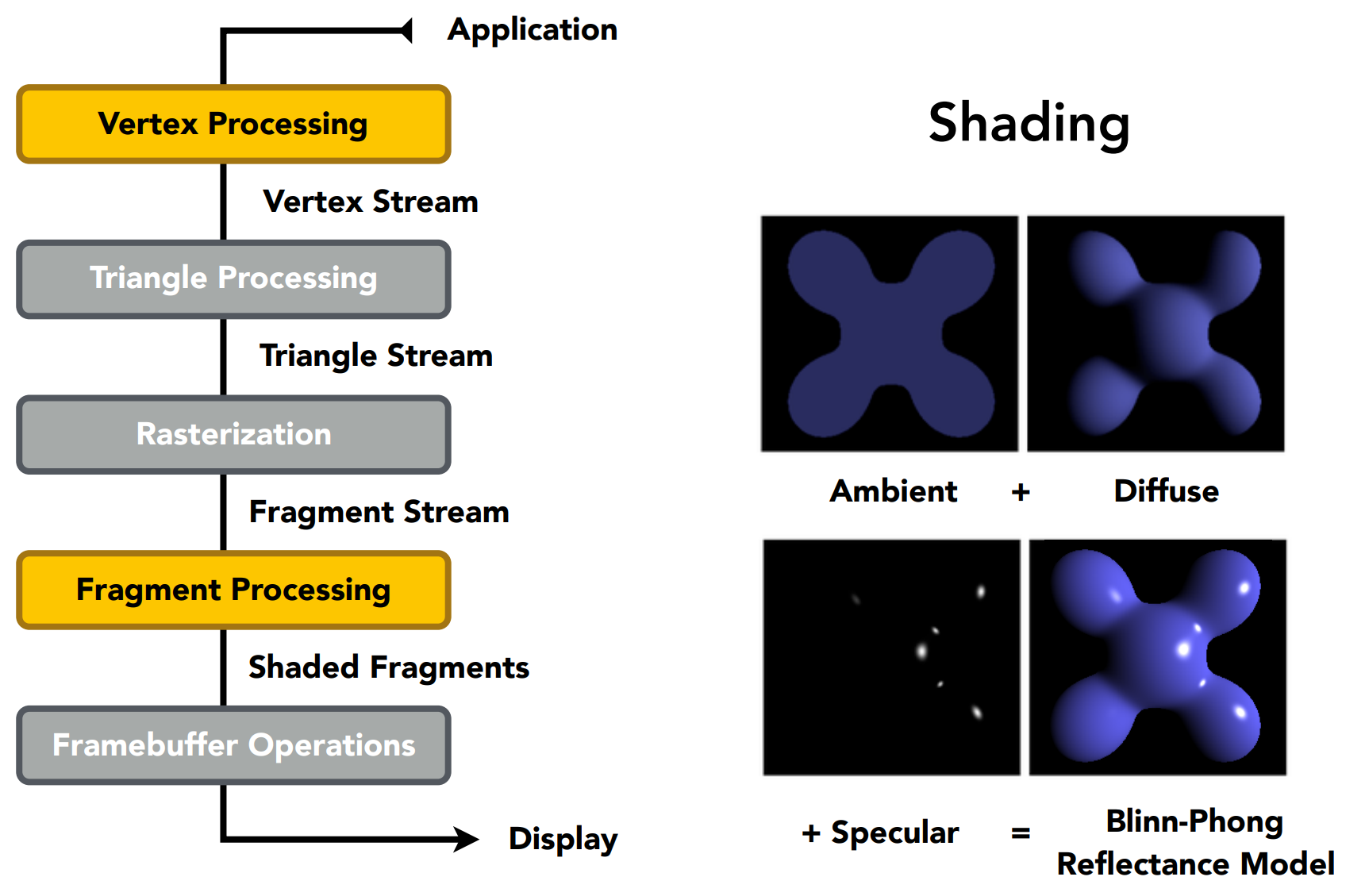
Shading可在Vertex Processing阶段,也可在Fragment Processing阶段;
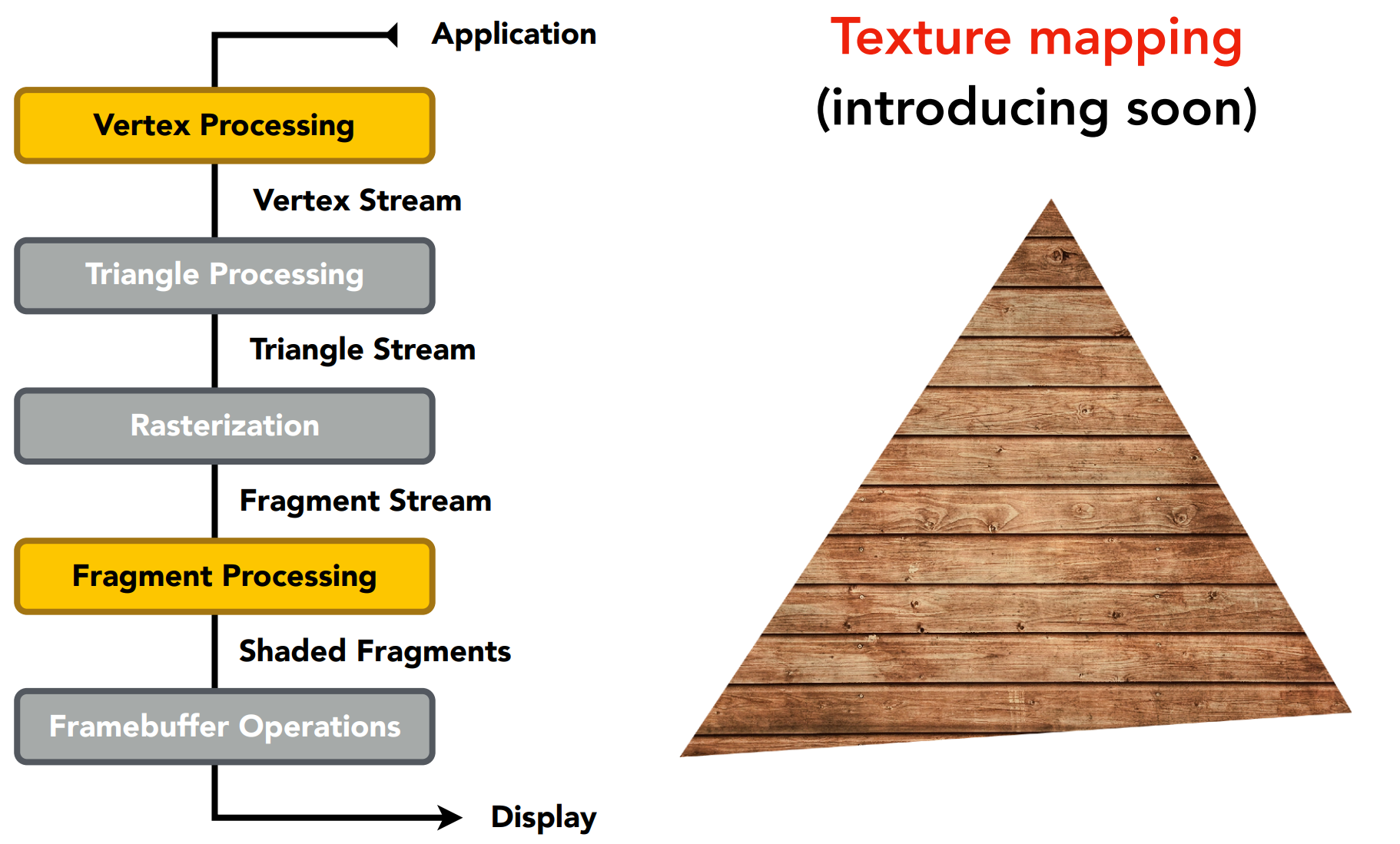
Texture mapping
Shader:

优秀Shader(到时候好好学习一下)
- Inigo Quilez, https://youtu.be/XuSnLbB1j6E
Lecture 08/09 Shading(Texture Mapping)
- 可见 百人计划-图形1.3-纹理的秘密 作为补充;
a). Interpolation Across Triangles: Barycentric Coordinates
重心插值的作用:通过顶点特定的值(normal、Color、Depth、Texture coordinates…),得到三角形内部片元(像素)上平滑过渡的值;
数学基础:
- 共面需满足的条件:
- $α+β+γ=1$,如需要点在三角形内,还需满足$α>0,β>0,γ>0$
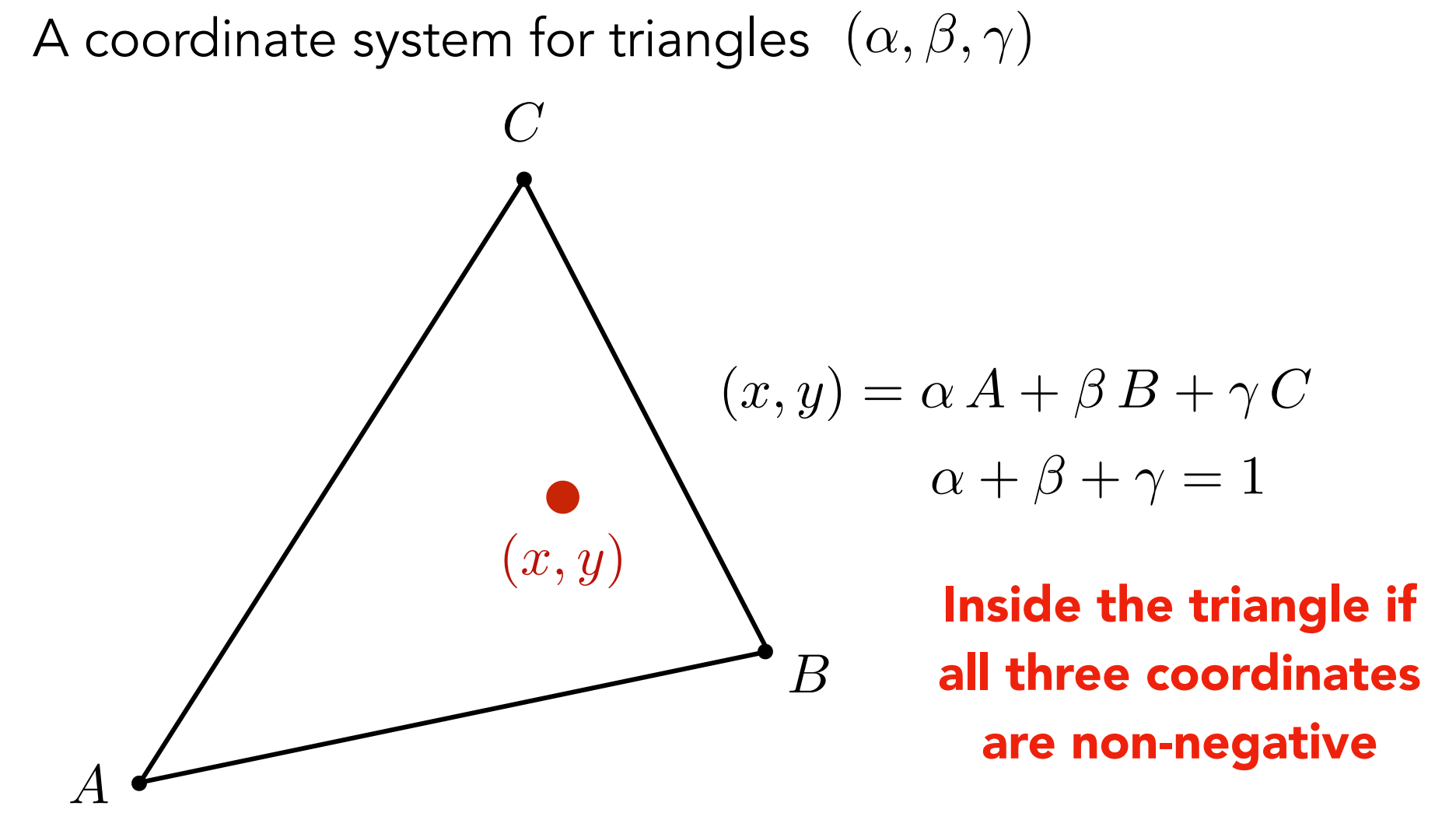
- $α+β+γ=1$,如需要点在三角形内,还需满足$α>0,β>0,γ>0$
- 重心坐标求法:
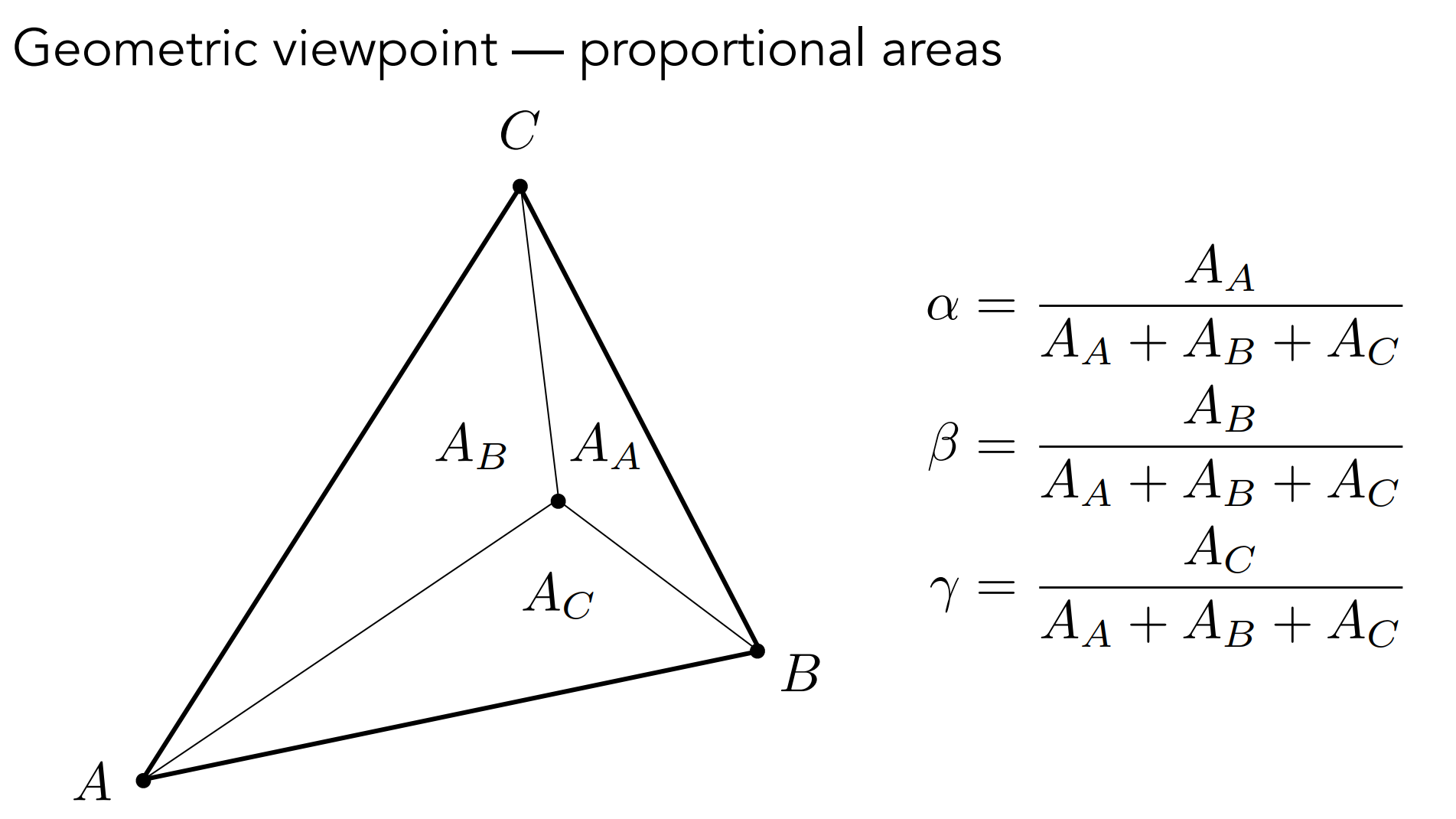
- 由以上易得,重心坐标$\begin{aligned}(x, y) &=\frac{1}{3} A+\frac{1}{3}B+\frac{1}{3} C\end{aligned}$
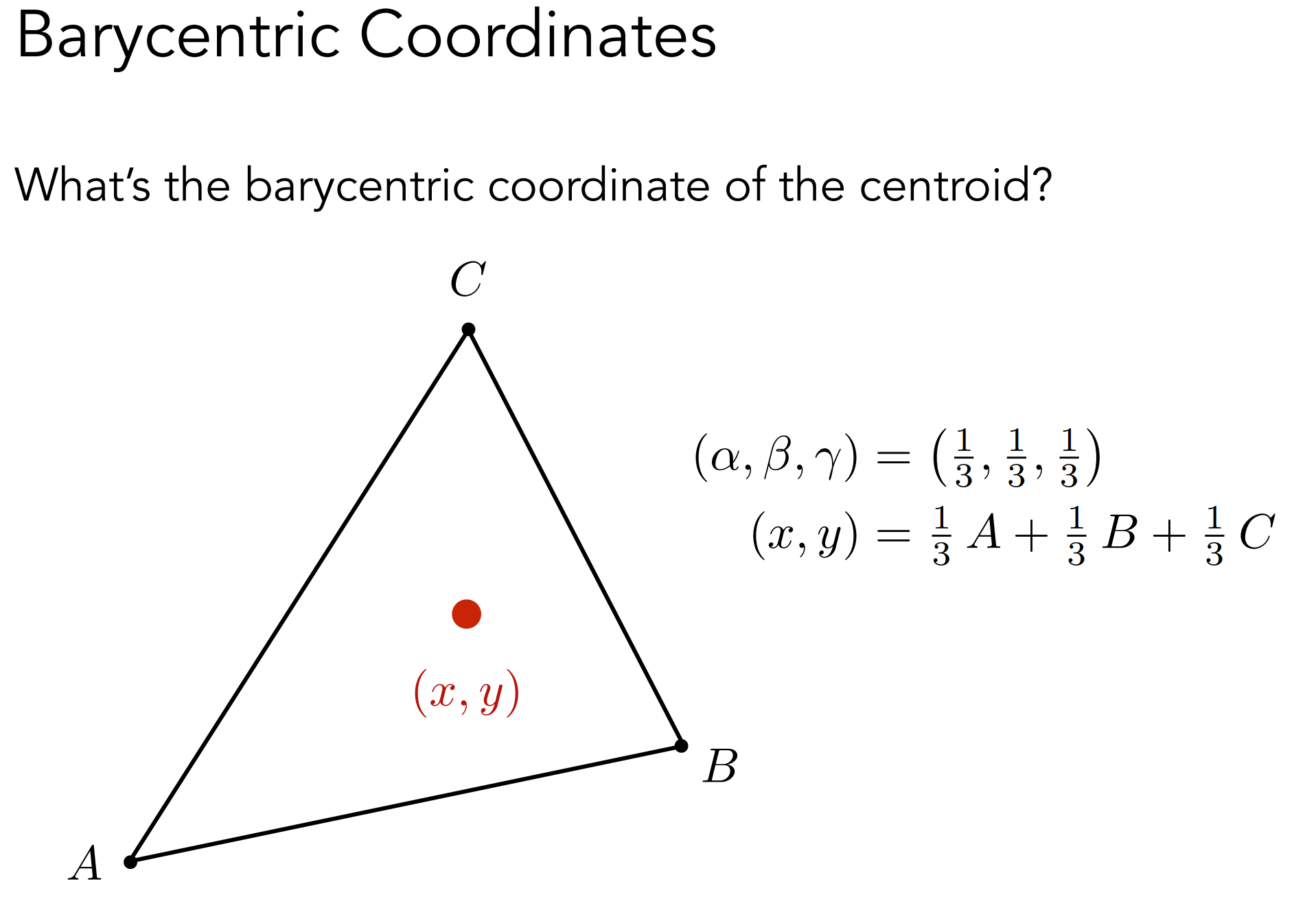
- 通用计算公式:
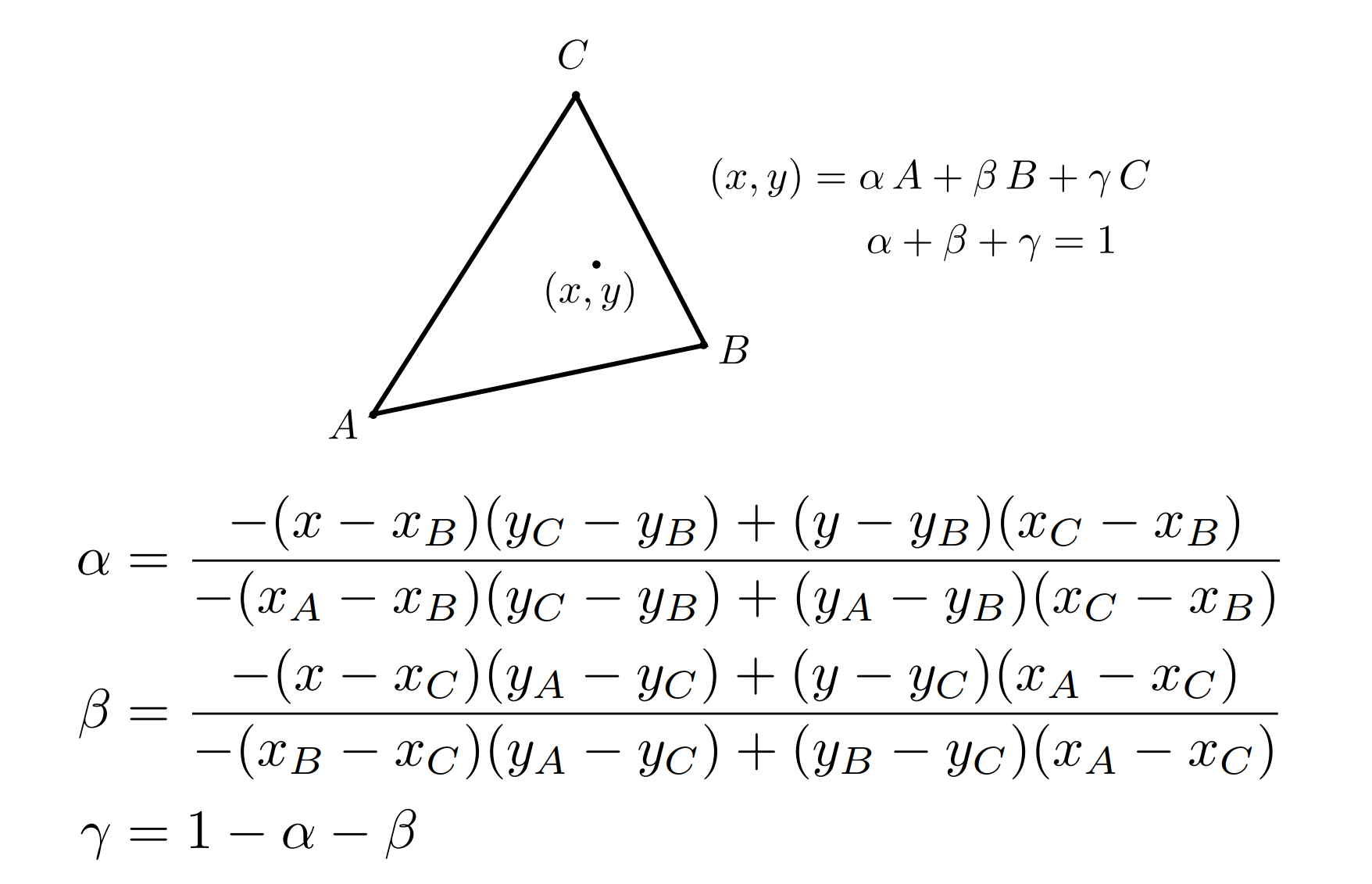
- Final:
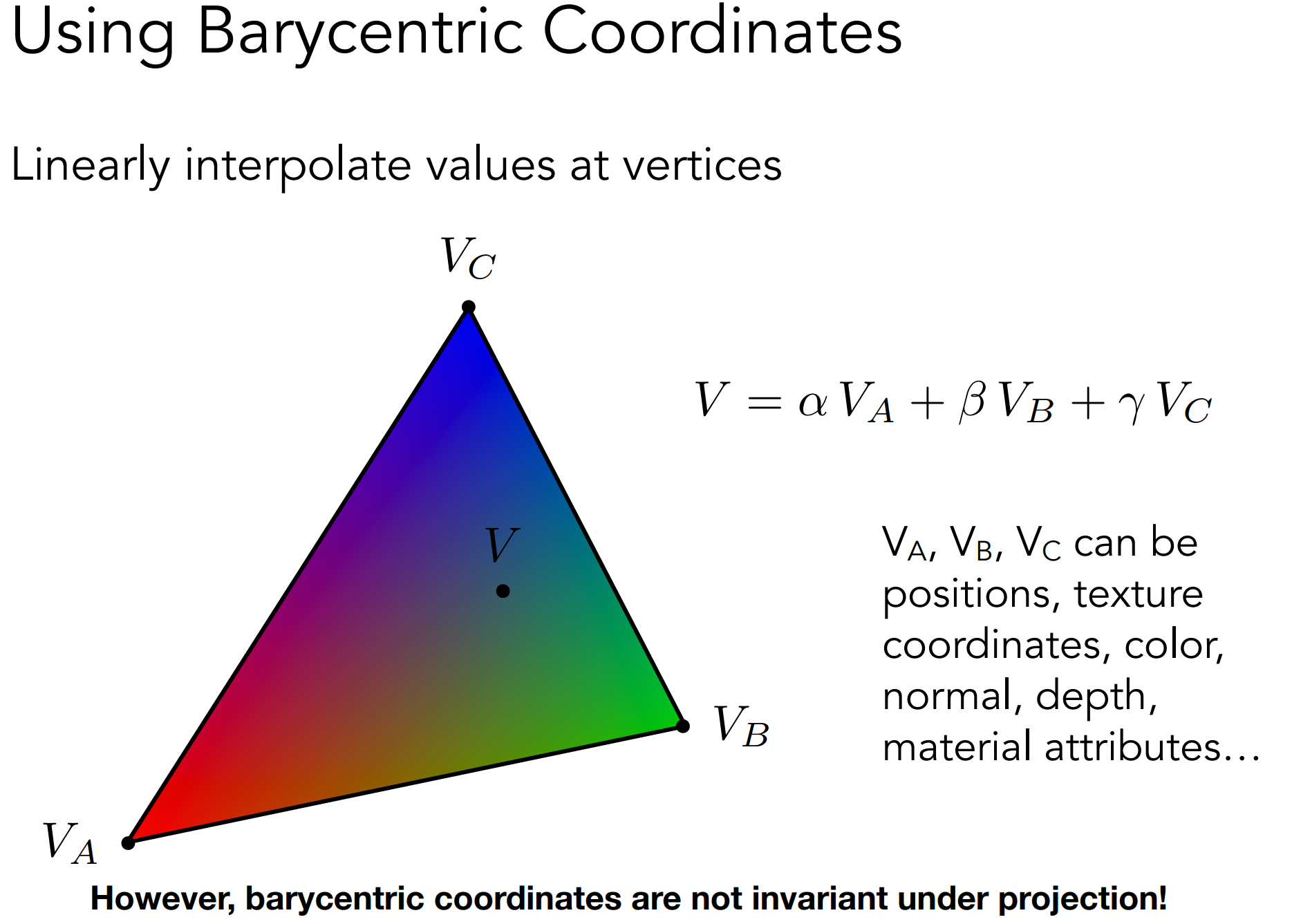
- 注意:重心并没有投影不变性,因此进行插值需要在三维空间中进行,而不是在屏幕的二维投影上;
- 共面需满足的条件:
b). Texture Magnification(需要放大纹理的情况)
- 对应情况:纹理过小(如距离物体近,而贴图小)
- 插值方式:
- Nearest
- Bilinear
- Bicubic
b.1). Bilinear Interpolation
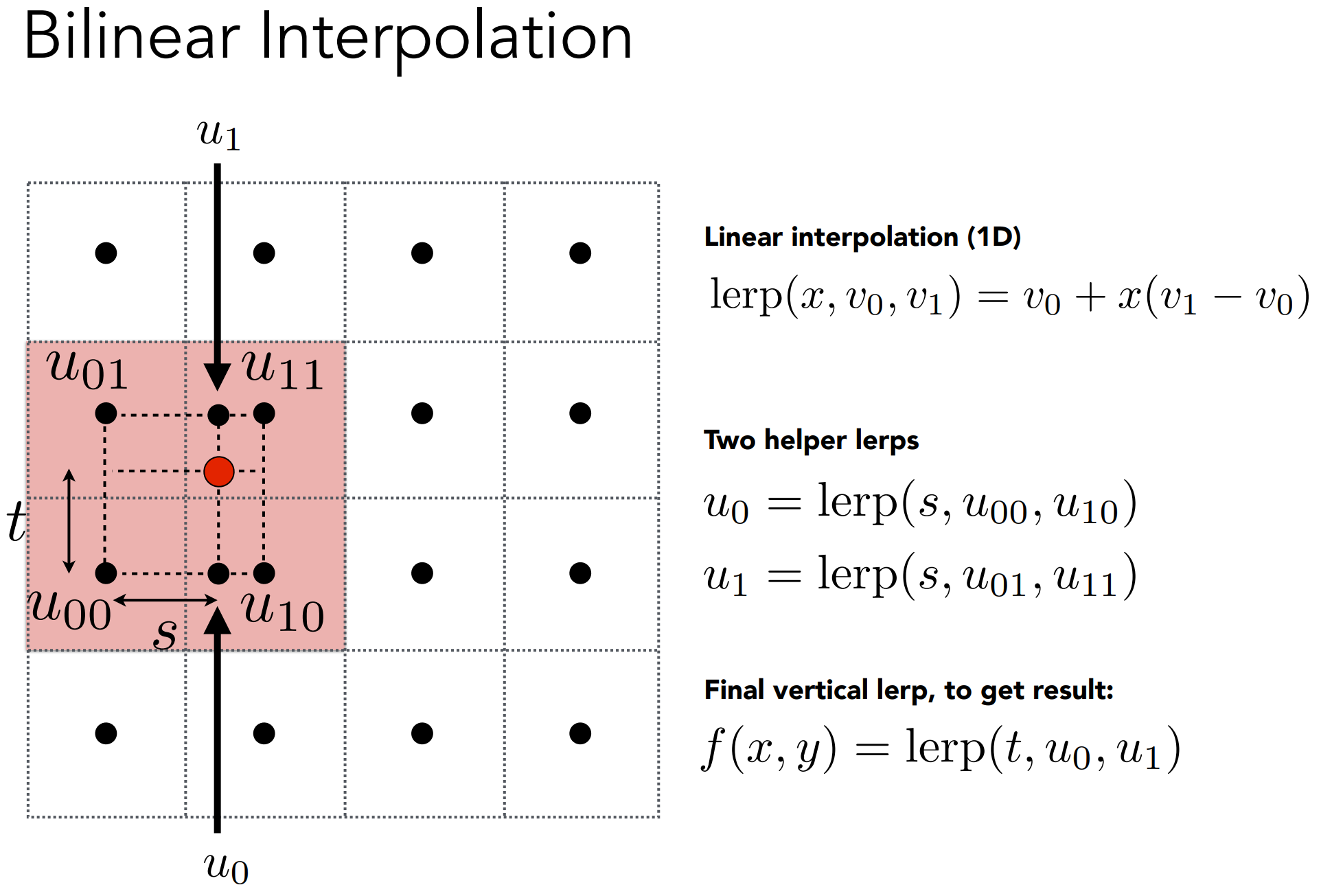
c). Texture Magnification(需要缩小纹理的情况)
对应情况:纹理过大(如距离物体远,而贴图大)
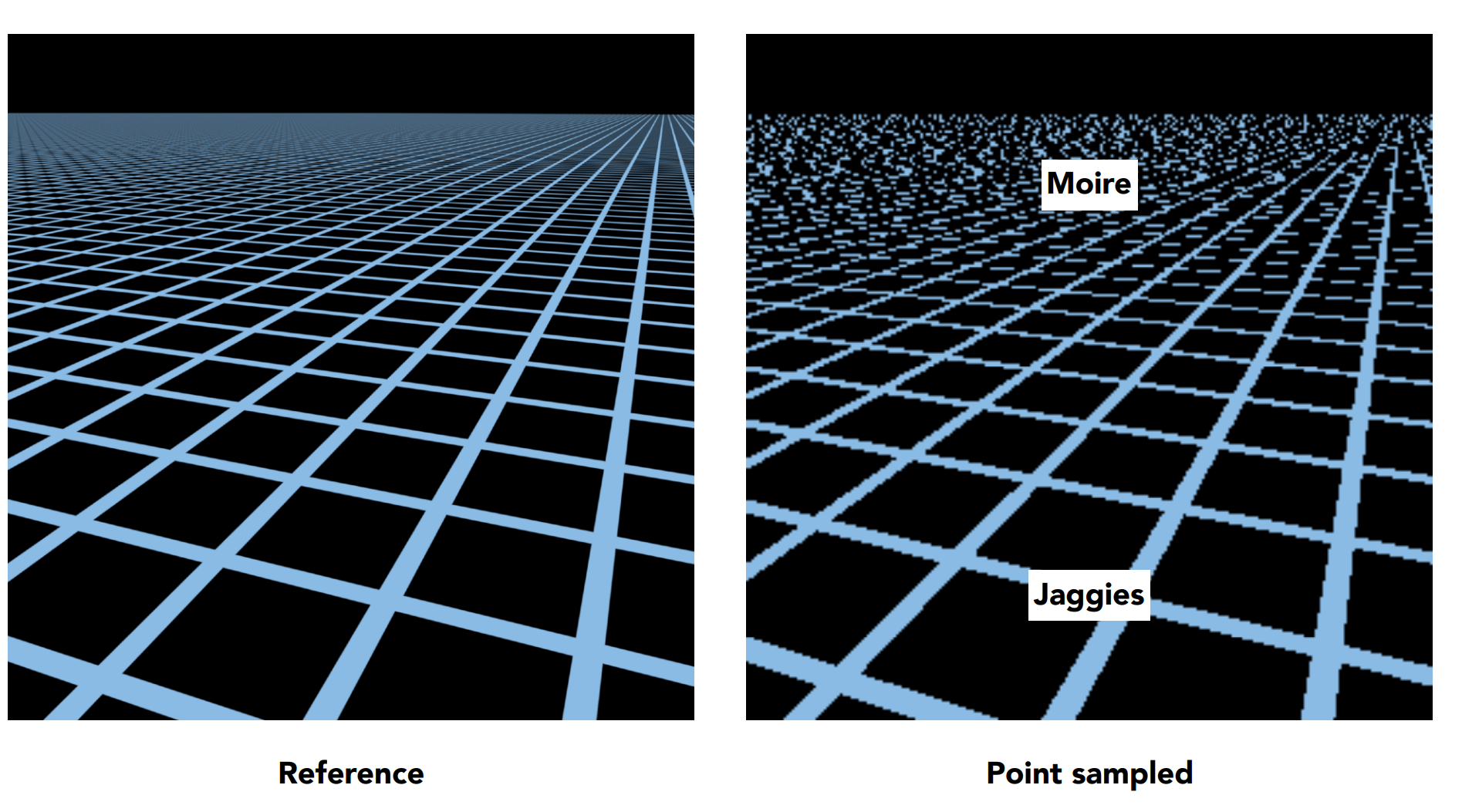
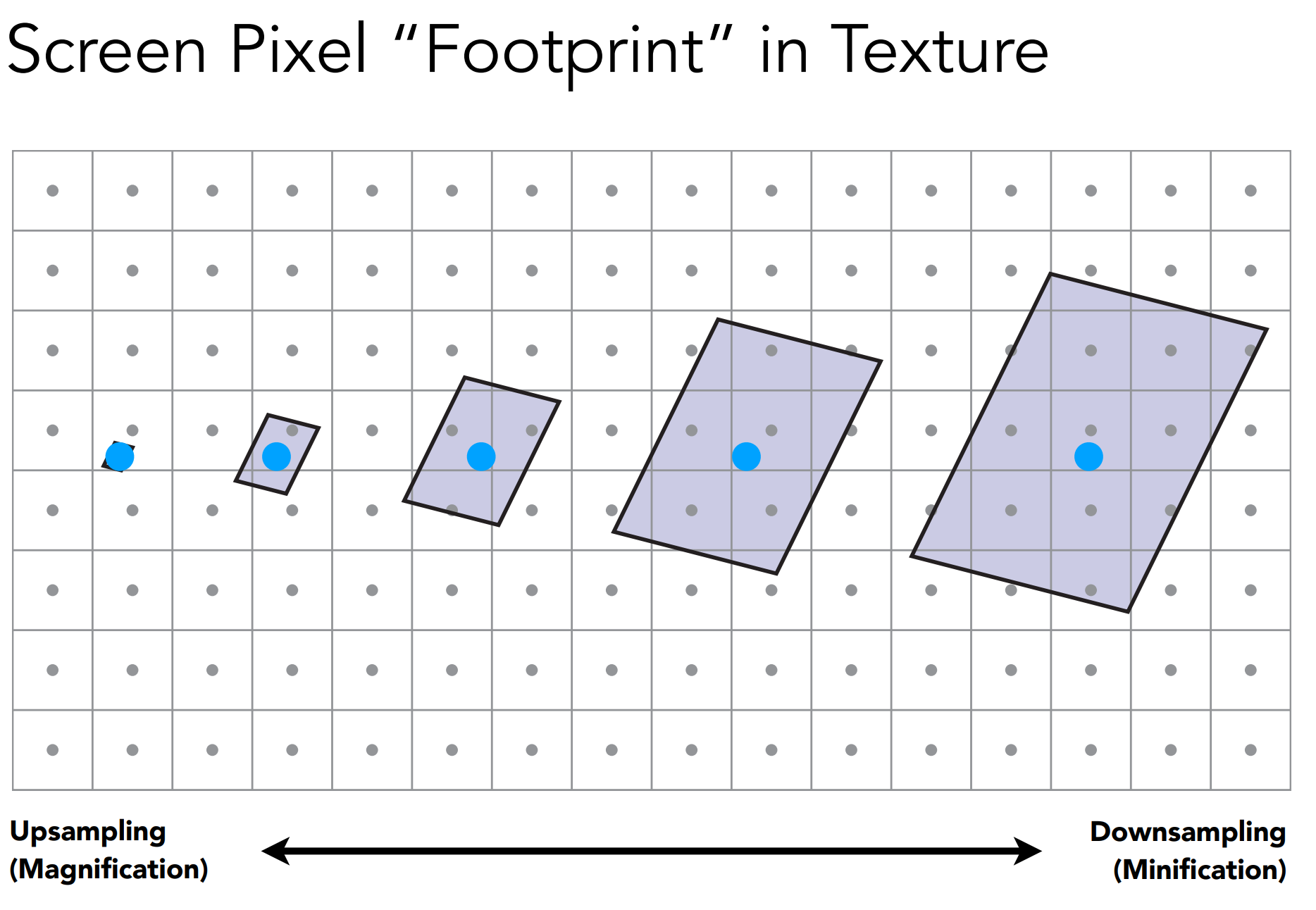
解决思路:
- 增大采样率(超采样)
- 高质量,但性能开销大;
- 减小贴图频率(Mipmap)
- 增大采样率(超采样)
c.1). Mipmap
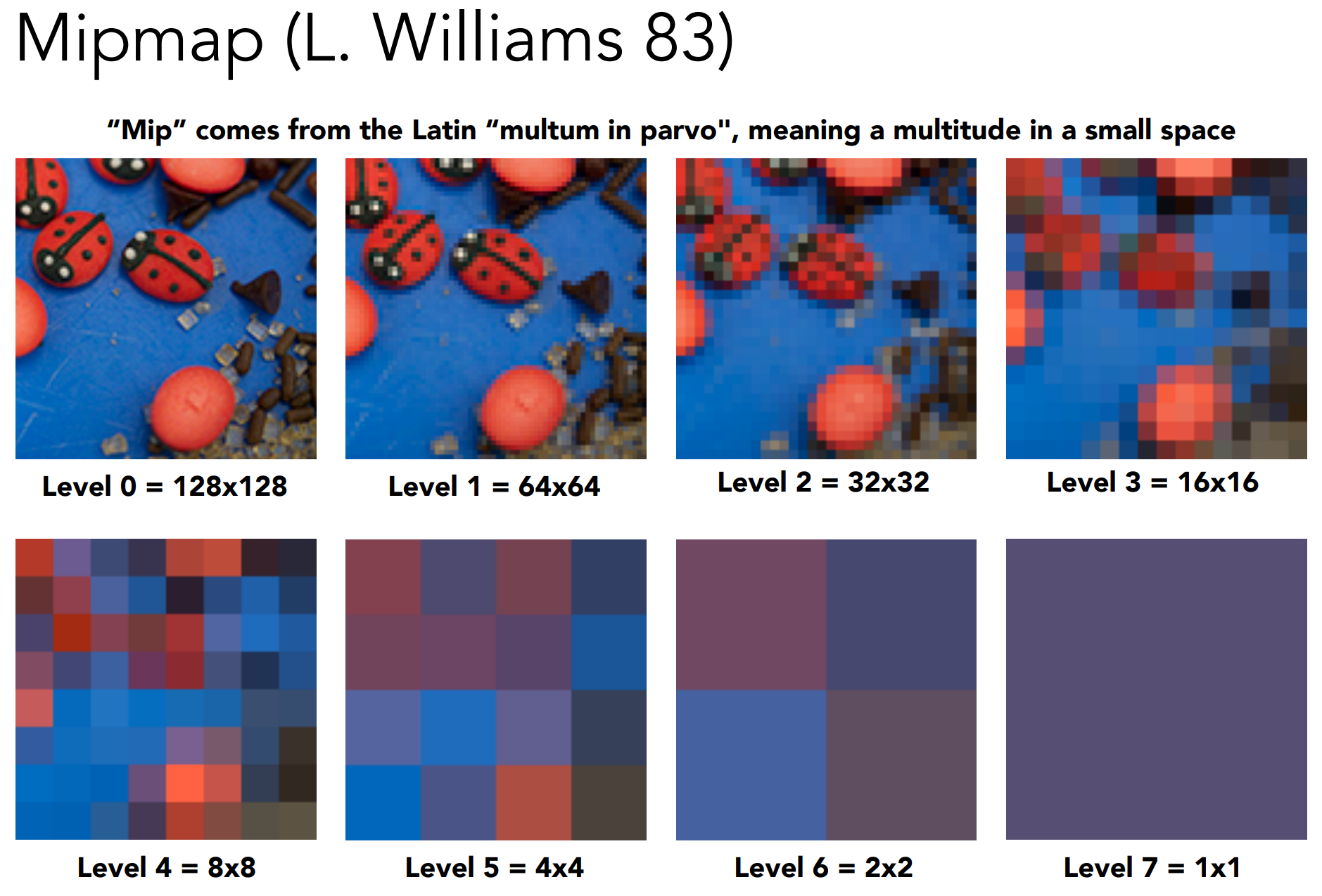
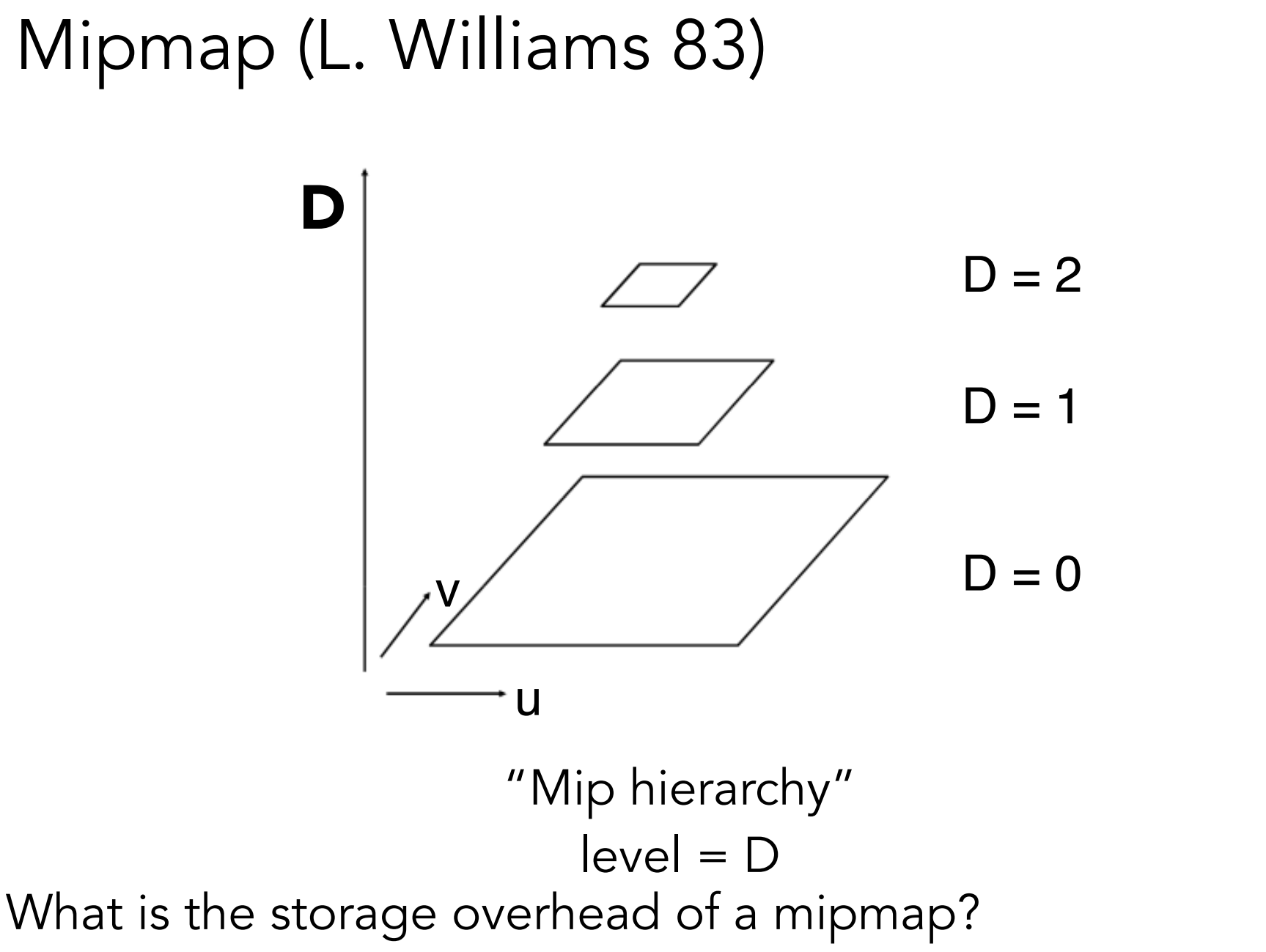
c.1). 如何确定Mipmap的level(参考百人计划):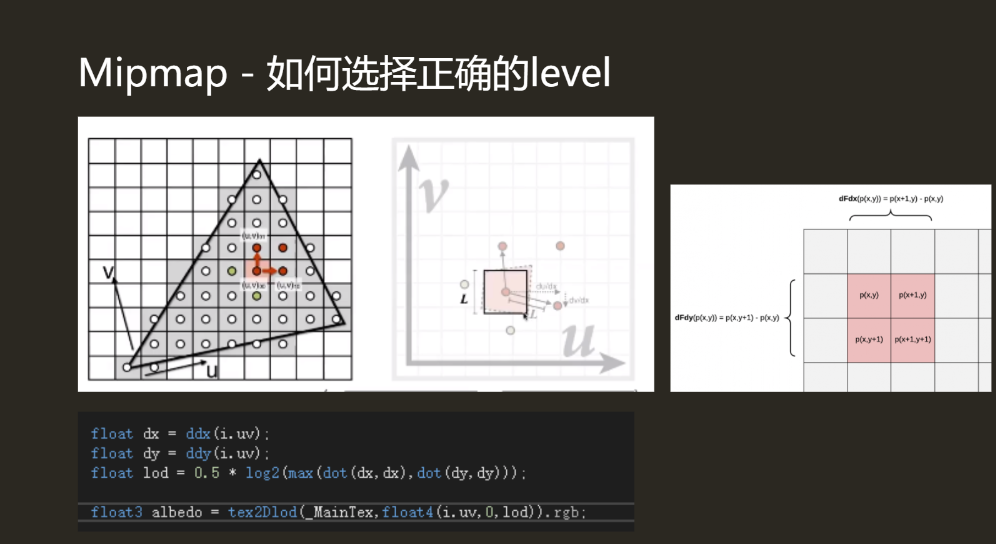
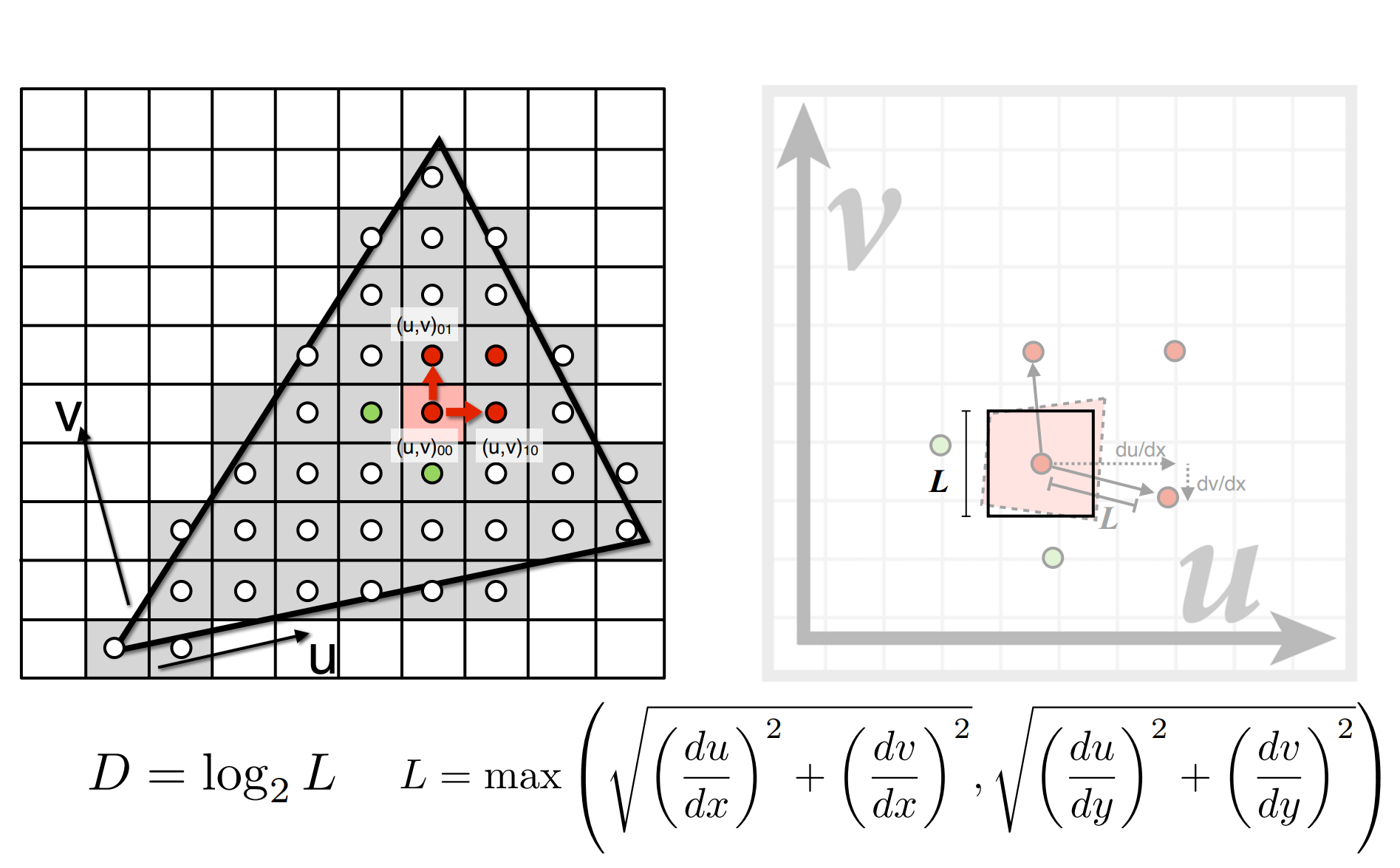
c.2). Mipmap之间的过渡
Visualization of Mipmap Level(D rounded to nearest integer level):

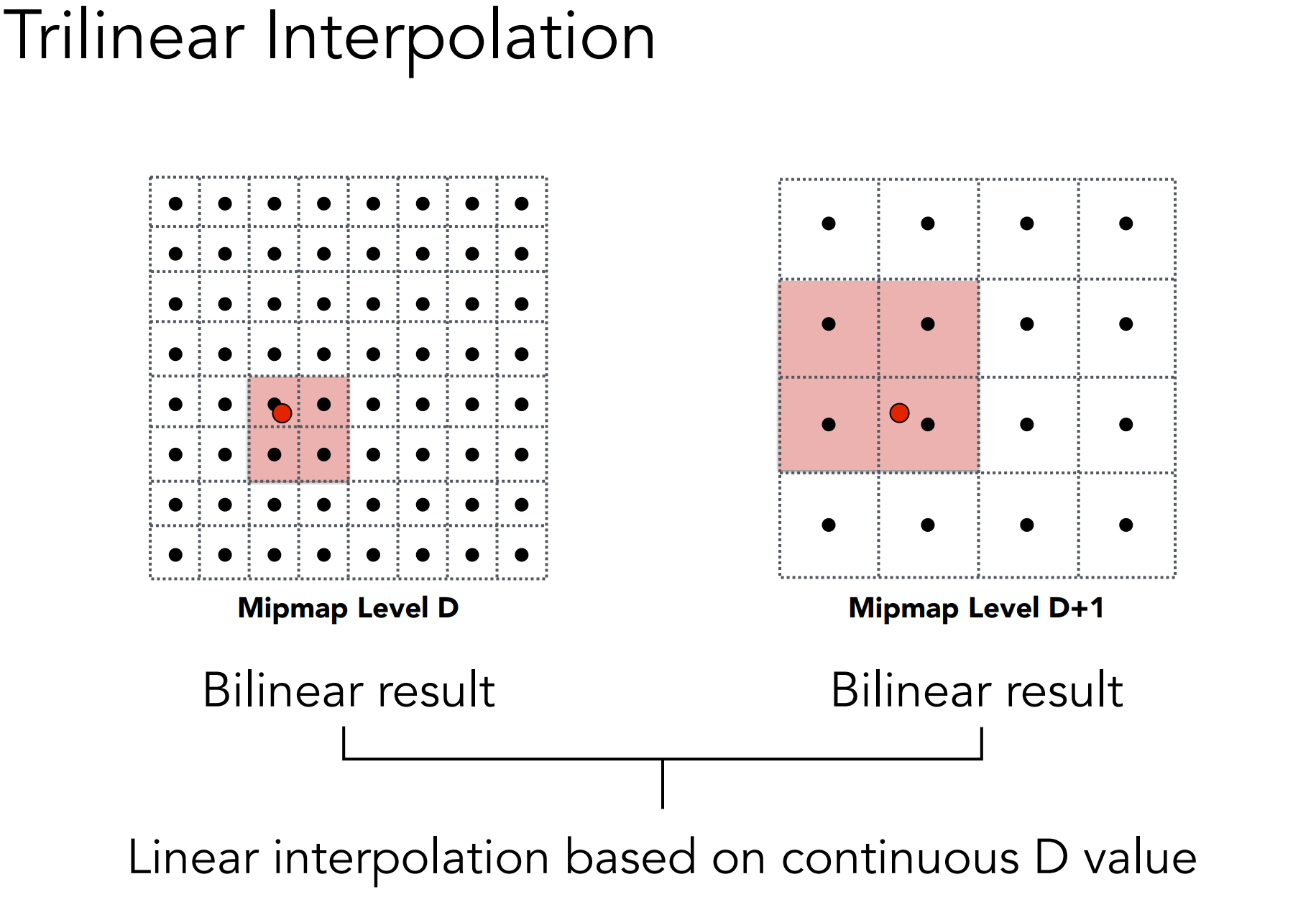
Trilinear Interpolation
- 作法:对相邻两层的Mipmap做Bilinear Interpolation,根据所得的level,对相邻两层进过插值的结果再进行一次插值;(e.g. D=1.6,则对一层和二层分别进行双线性插值后,再进行$lerp(1.6-1, n_1, n_2)$)
- Final:

- 作法:对相邻两层的Mipmap做Bilinear Interpolation,根据所得的level,对相邻两层进过插值的结果再进行一次插值;(e.g. D=1.6,则对一层和二层分别进行双线性插值后,再进行$lerp(1.6-1, n_1, n_2)$)
d). Applications of Textures
d.1). Environment Map
- 简介:

- 对于环境光源,我们认为它来自与无限远处,即没有深度意义,不同位置的同一方向受到的环境光源相同(当然,暂不考虑遮挡)
- Spherical Environment Map:

- Problem:不是均匀的描述,在极点会存在较大的扭曲;

- Problem:不是均匀的描述,在极点会存在较大的扭曲;
- CubeMap:
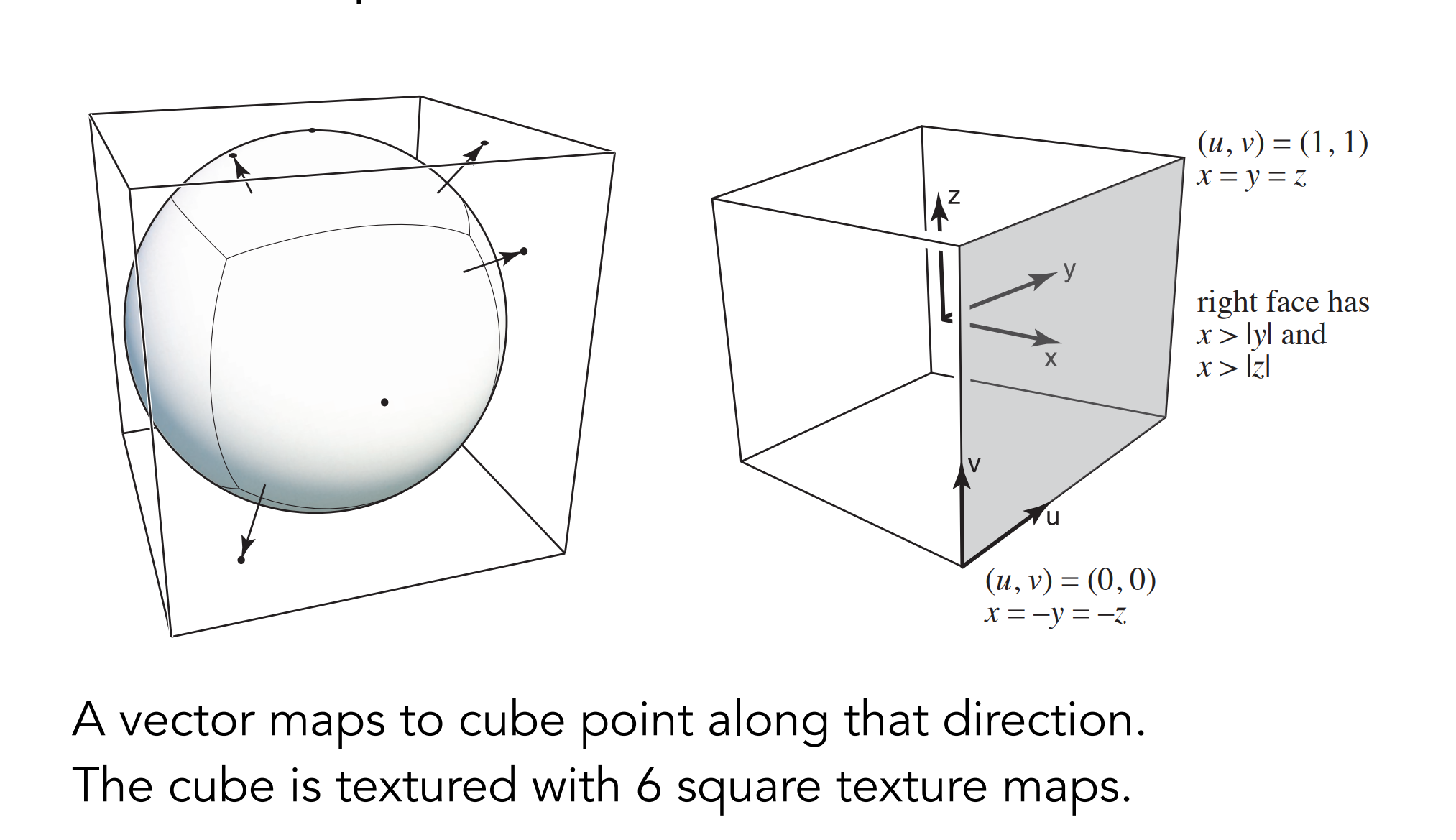

d.2). Bump Mapping

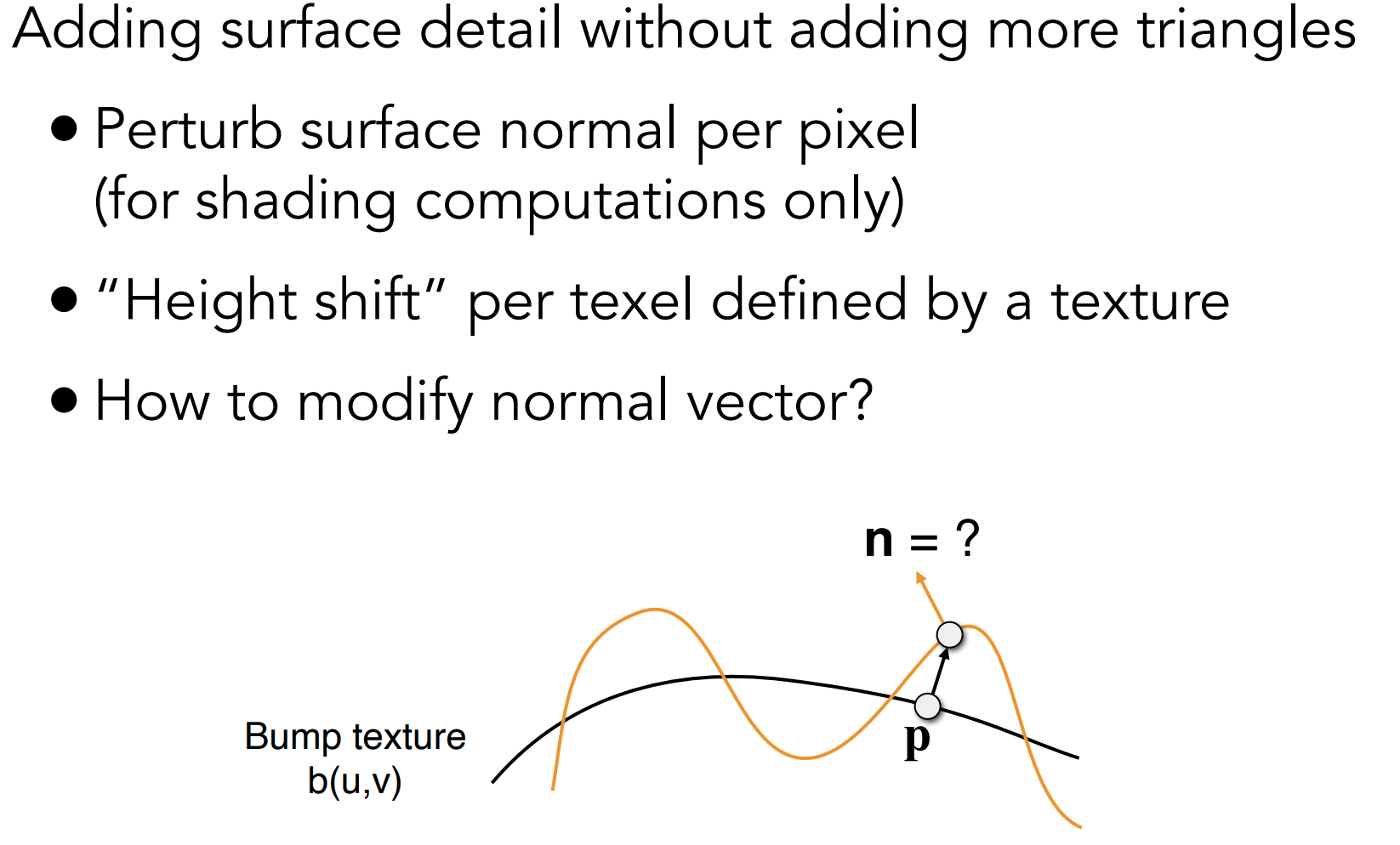
凹凸贴图(视差贴图/法线贴图)计算法线过程:
思路(一维情况,in flatland):
- 原始法线 $n(p)=(0,1)$
- 在 p 点的导数 $dp=c·[h(p+1)-h(p)]$ ($c$ 是常数,用于缩放导数,改变其影响程度),得出切线
- 计算法线(垂直于切线) $n(p)=(-dp,1).normalized()$;
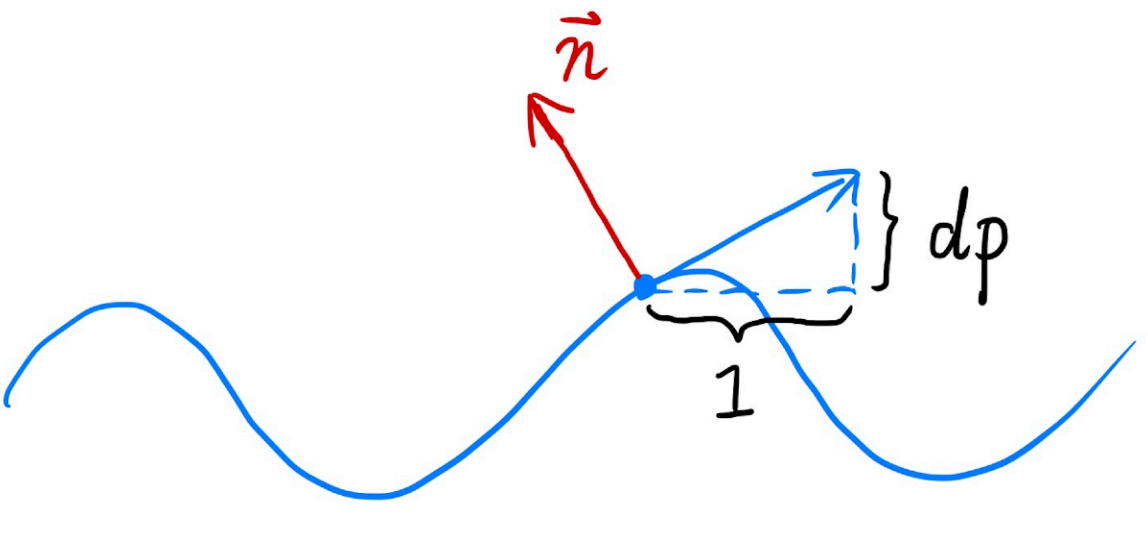
思路(in 3D):
- 原始法线 $n(p)=(0,0,1)$;
- 纹理上的点对 $u$ 方向和 $v$ 方向求偏导,得出切线
- $dp/du=c1·[h(u+1)-h(u)]$
- $dp/dv=c2·[h(v+1)-h(v)]$
- 计算法线(垂直于切线) $n(p)=(-dp/du,-dp/dv,1).normalized()$;
以上计算均在切线空间、局部空间计算(具体看冯-入门精要)
Displacement mapping(置换/高度贴图):
- 需要足够多的三角面(DX中的Dynamic Tessellation,动态曲面细分)
- 真正地移动了顶点
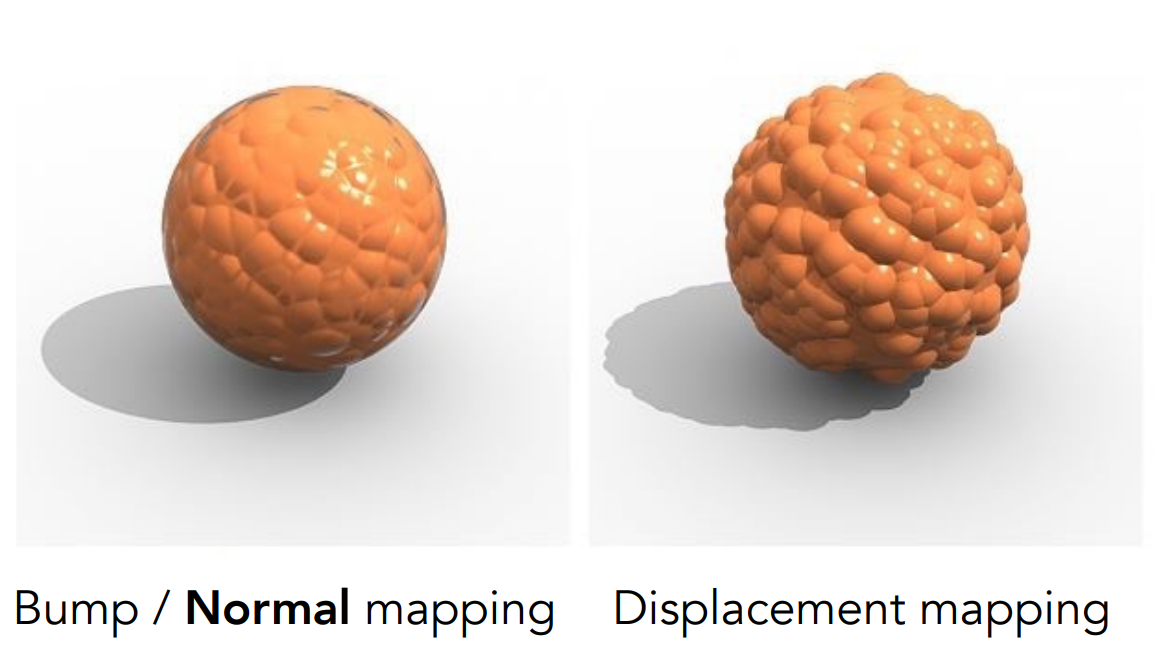
d.3). 3D Procedural Noise + Solid Modeling
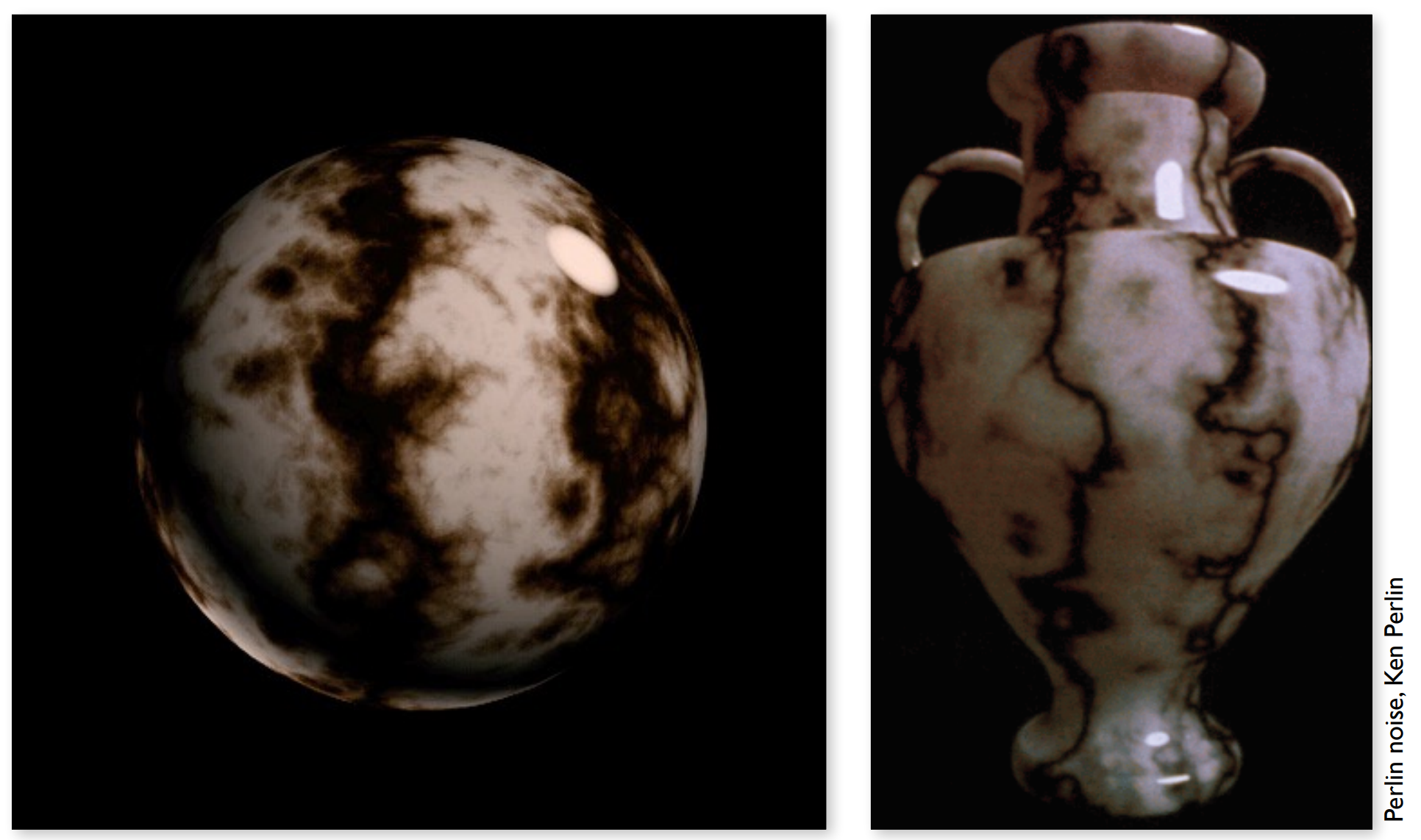
- Perlin noise
d.4). Provide Precomputed Shading
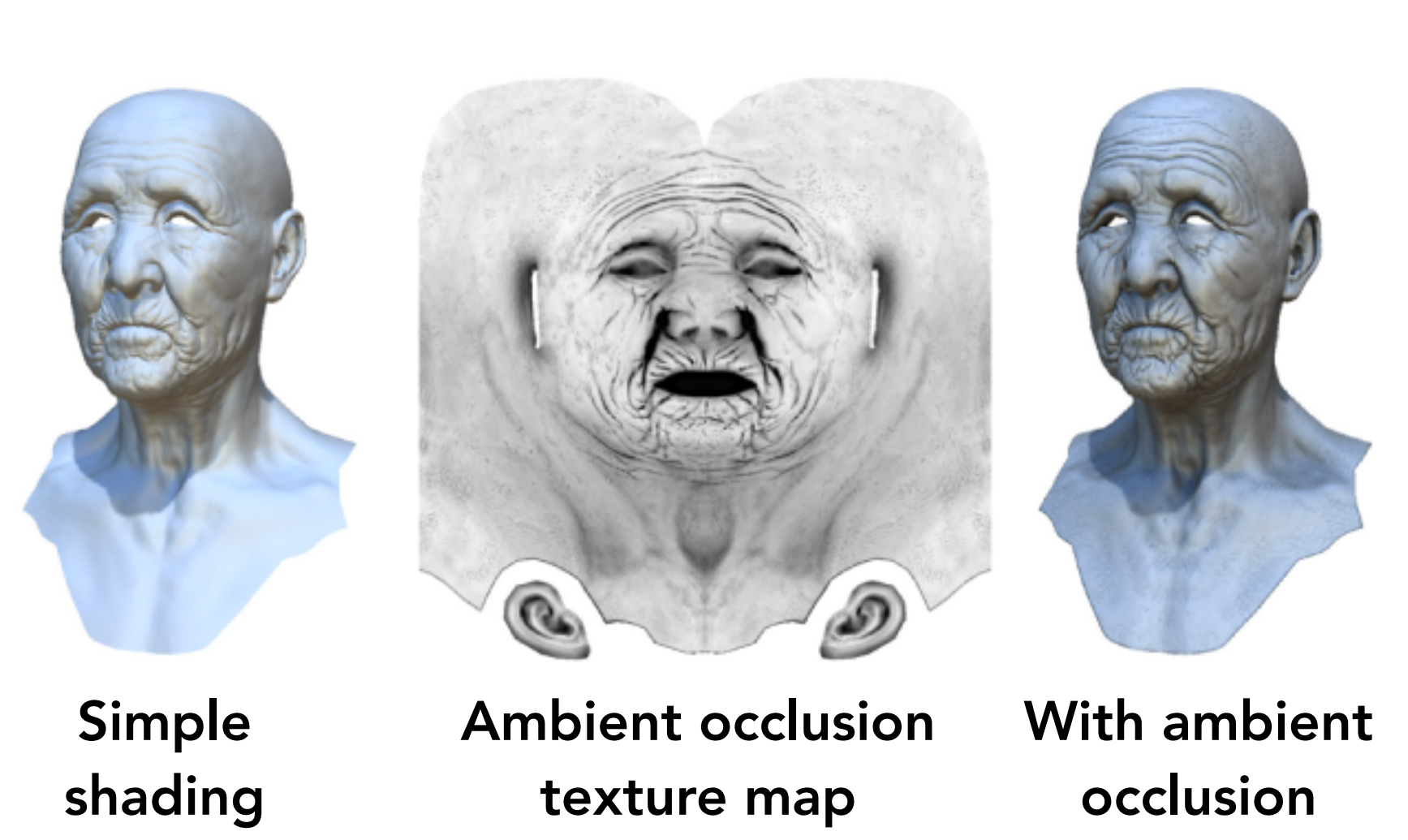
- 使用Baking的AO等(也可记录其他信息,如SP中的ID、Position、Curvature等);
d.5). 3D Textures and Volume Rendering
- 体渲染