Games101_10_12 Geometry
Lecture 10/11: Geometry 1 2
- 不可能所有物体都用三角面表示,一些复杂的物体如毛发、水滴等用三角面表示开销极大;
a). 几何的表示形式
- 隐式(Implicit)
- algebraic surface
- level sets
- distance functions
- …
- 显式(Explicit)
- point cloud
- polygon mesh
- subdivision, NURBS
- …
b). 几何的隐式表示(Implict Representations of Geometry)
- 基于归类的点
- 点满足某种特定的关系,但不给你特定的点
- e.g. Sphere: 所有三维中的点,满足 $x^2+y^2+z^2=1$;
- 通用情况:$f(x,y,z)=0$
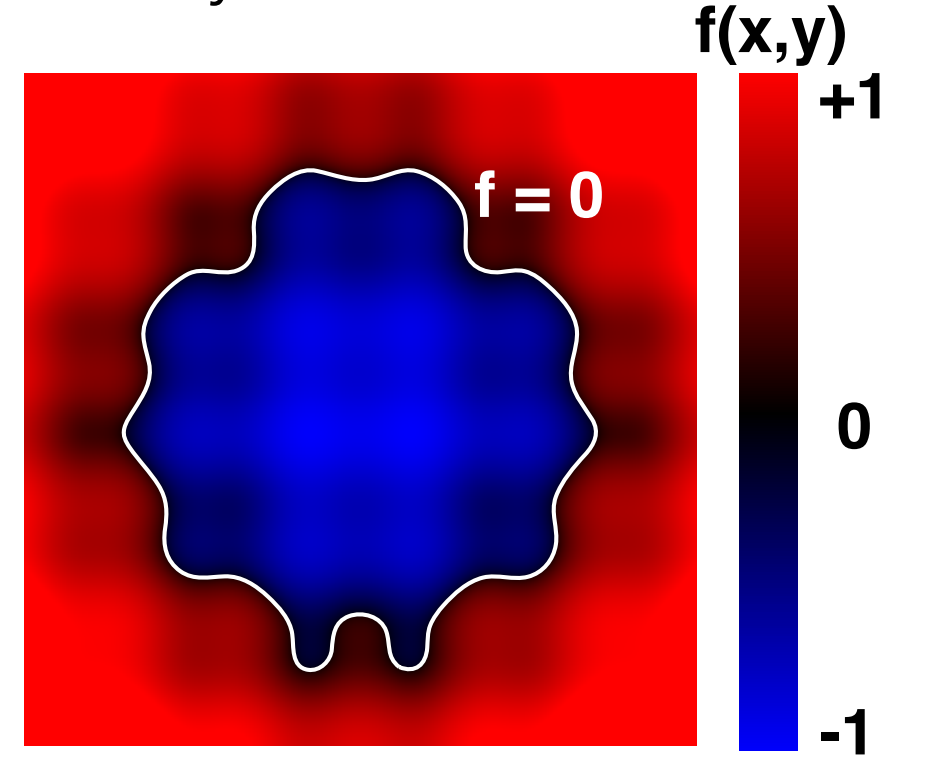
- 点满足某种特定的关系,但不给你特定的点
- 缺点:
- 难以采样(Sampling Can Be Hard,难以得到式子表示的整体形状)
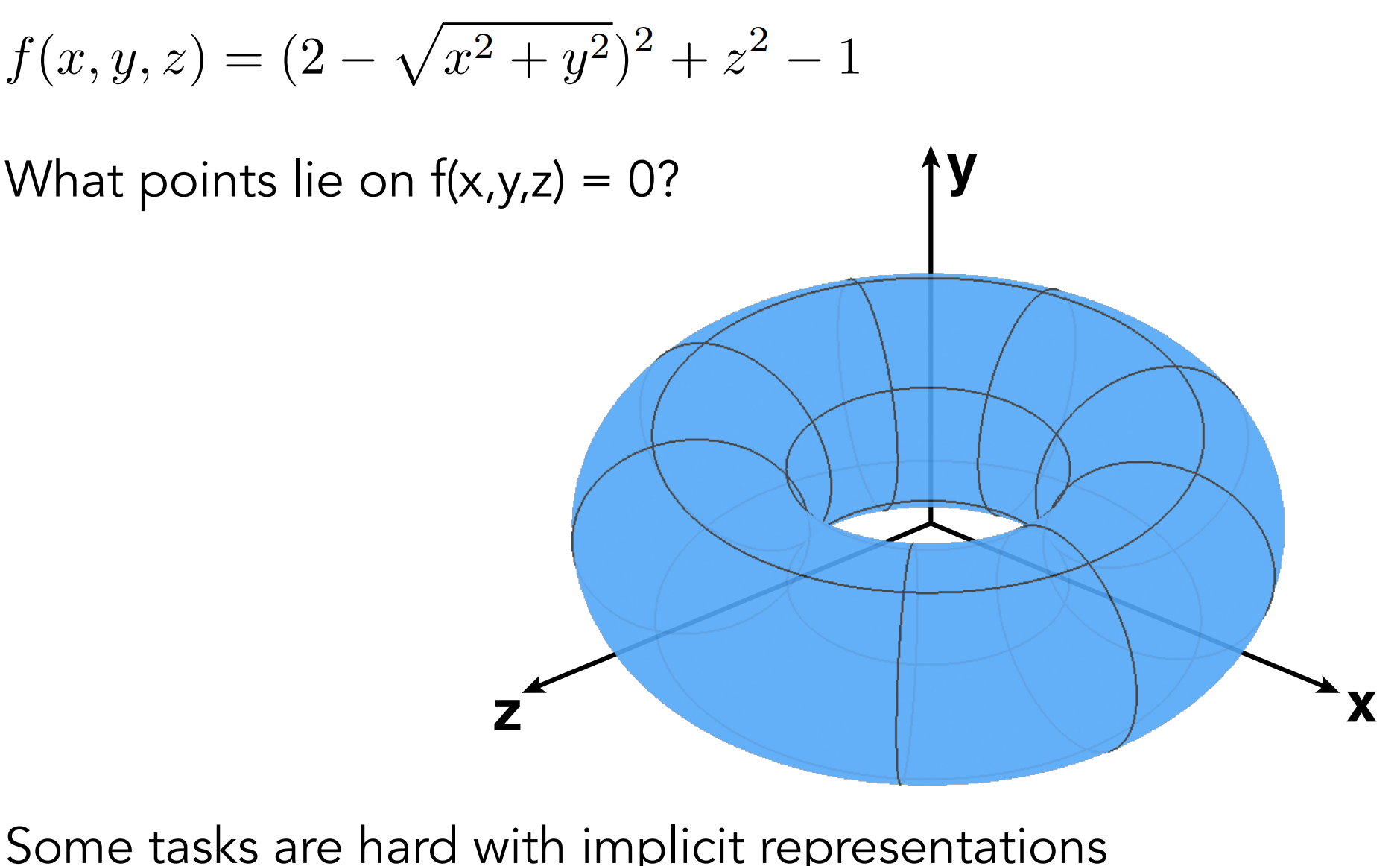
- 难以采样(Sampling Can Be Hard,难以得到式子表示的整体形状)
- 优点:
- 方便判断点是否在几何体内(Inside/Outside Tests Easy)
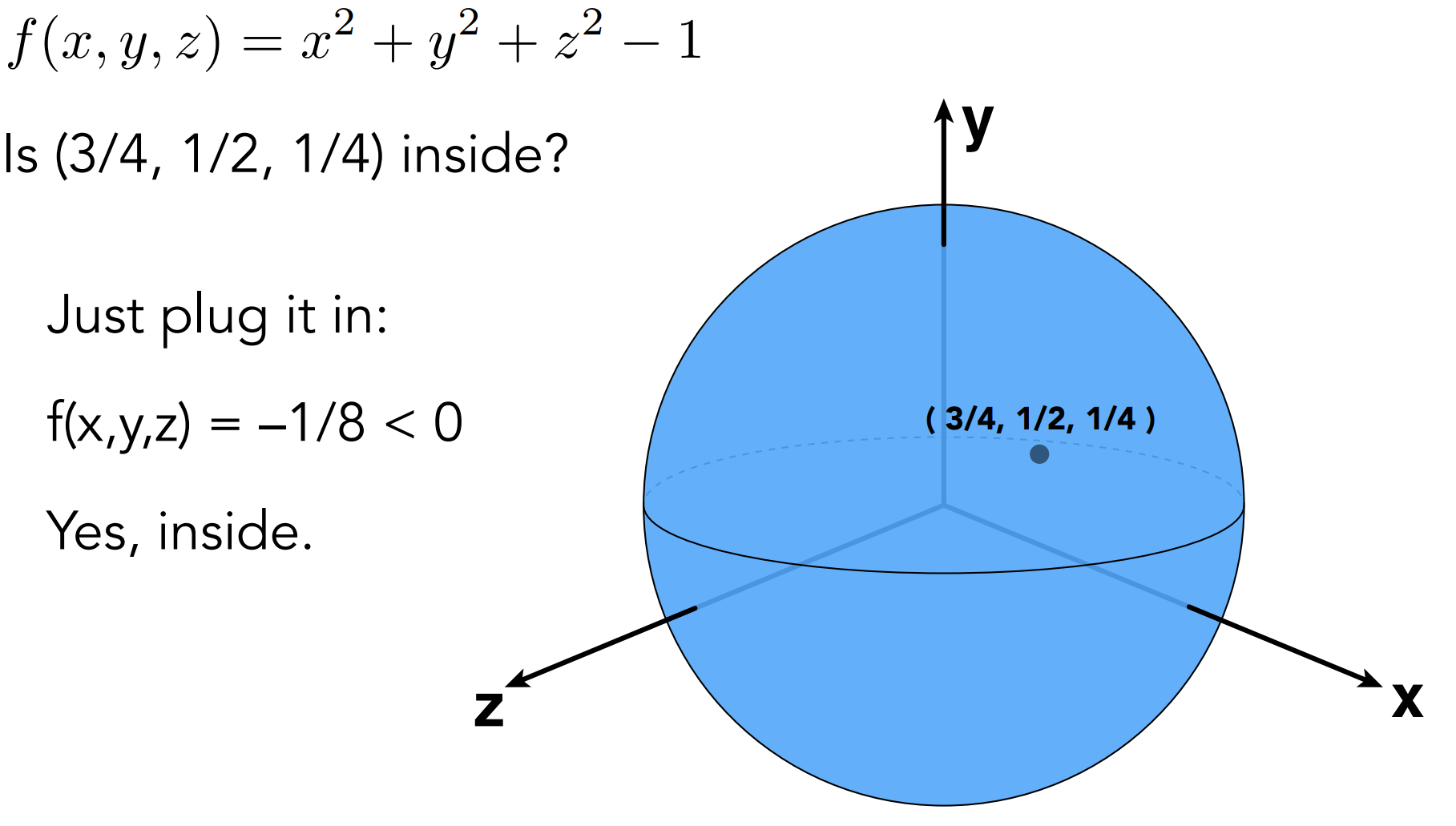
- 方便判断点是否在几何体内(Inside/Outside Tests Easy)
b.1). Algebraic Surfaces(曲面代数)

- 难以表达复杂的形状;
b.2). Constructive Solid Geometry(CSG, 体素构造表示形式)
- 对隐式几何体进行布尔运算;
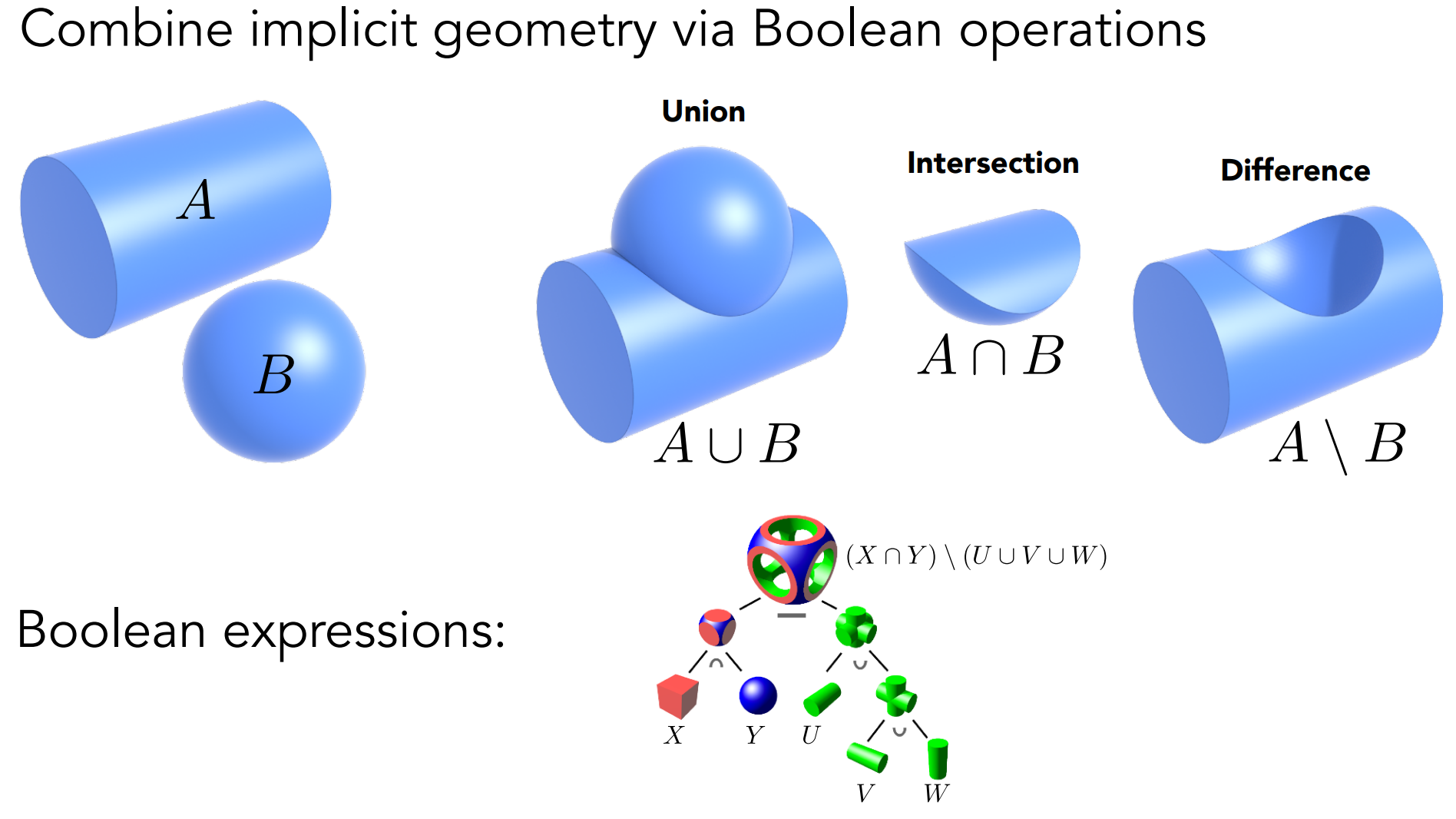
b.3). Distance Function(距离函数)

- 给出各个点到物体的最小距离
- Blending Distance Function:
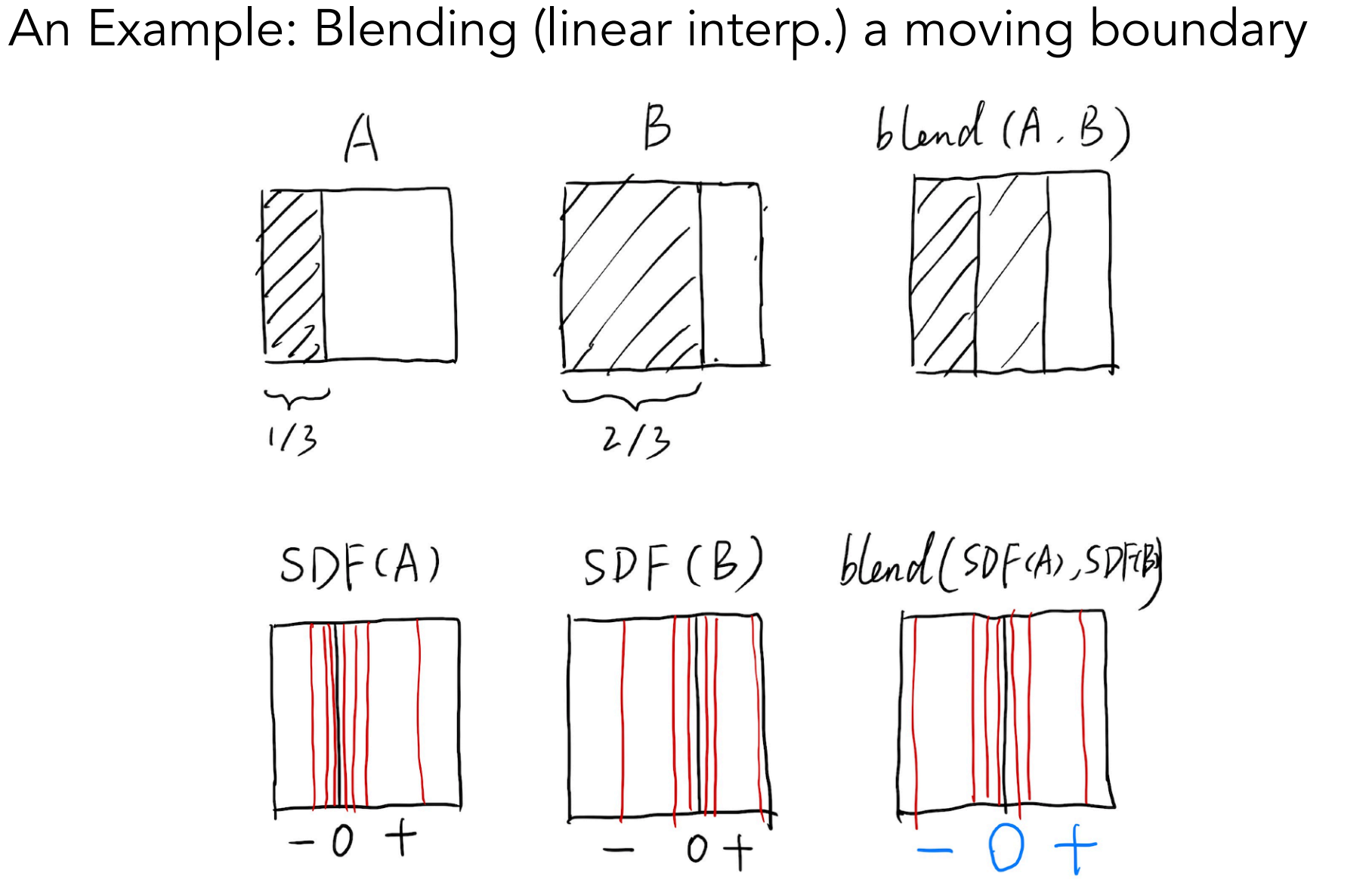
- 目的:通过混合得到A、B运动的中间状态;
- 上半部分,blend之后中间1/3是灰的,而理想的结果是左边1/2是黑色,右边1/2是白色
- 下半部分,对SDF进行混合,再将blend后的结果恢复成shape(找到SDF等于0的情况的所有点),就可得到中间状态的物体;

- 目的:通过混合得到A、B运动的中间状态;
- See https://iquilezles.org/www/articles/raymarchingdf/raymarchingdf.htm
b.4). Level Set Methods(水平集)
封闭方程(DF)很难描述复杂的形状
备选方案:存储近似函数值的网格(Level Set Methods)
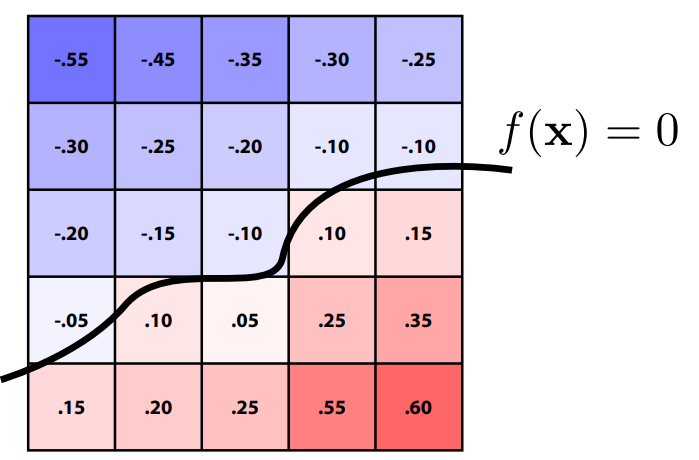
- 通过找到插值为0的位置确定表面;
- 提供对形状更明确的控制(如纹理)?
应用:
Level Sets from Medical Data (CT, MRI, etc. 三维LSM)
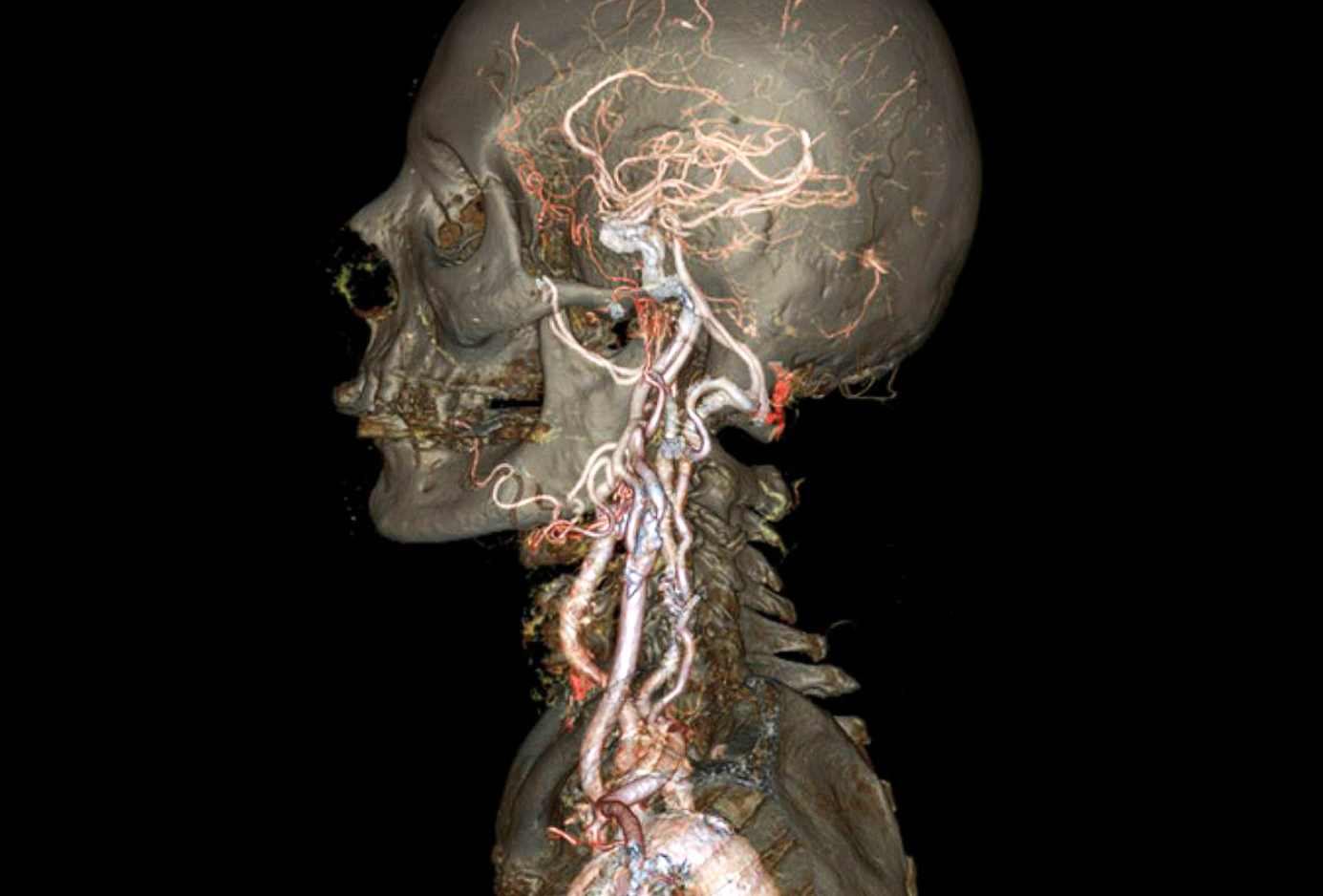
物理模拟:如水平集得到各点到液体边界的距离(距离函数混合水滴)

b.5). Fractals(分形)

c). 几何的显式表示(“Explicit” Representations of Geometry)
简介: 直接给出所有的点 或者 通过参数映射(via parameter mapping)
- 参数映射:给出uv,以及uv到三维空间的映射关系,遍历所有的uv就可找到三维空间所有的点;
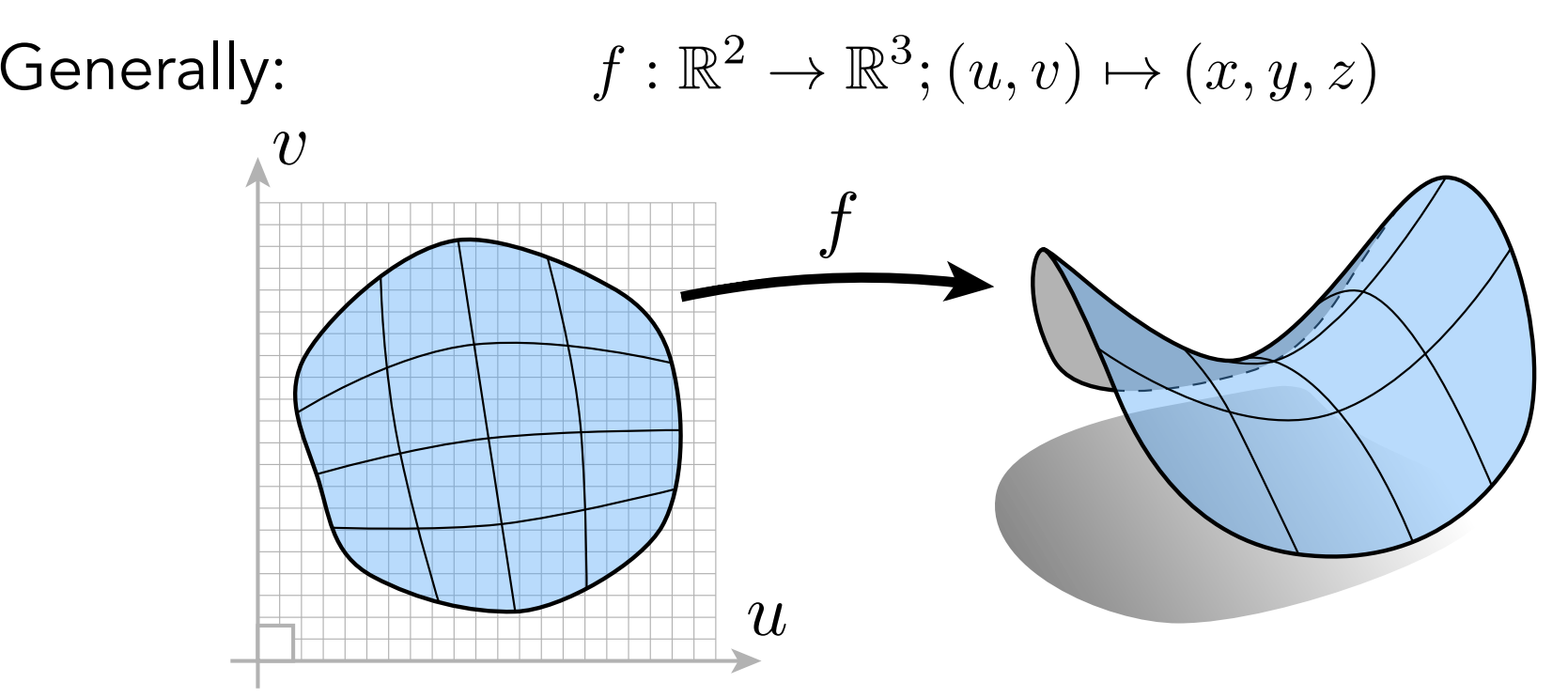
- 参数映射:给出uv,以及uv到三维空间的映射关系,遍历所有的uv就可找到三维空间所有的点;
采样简单
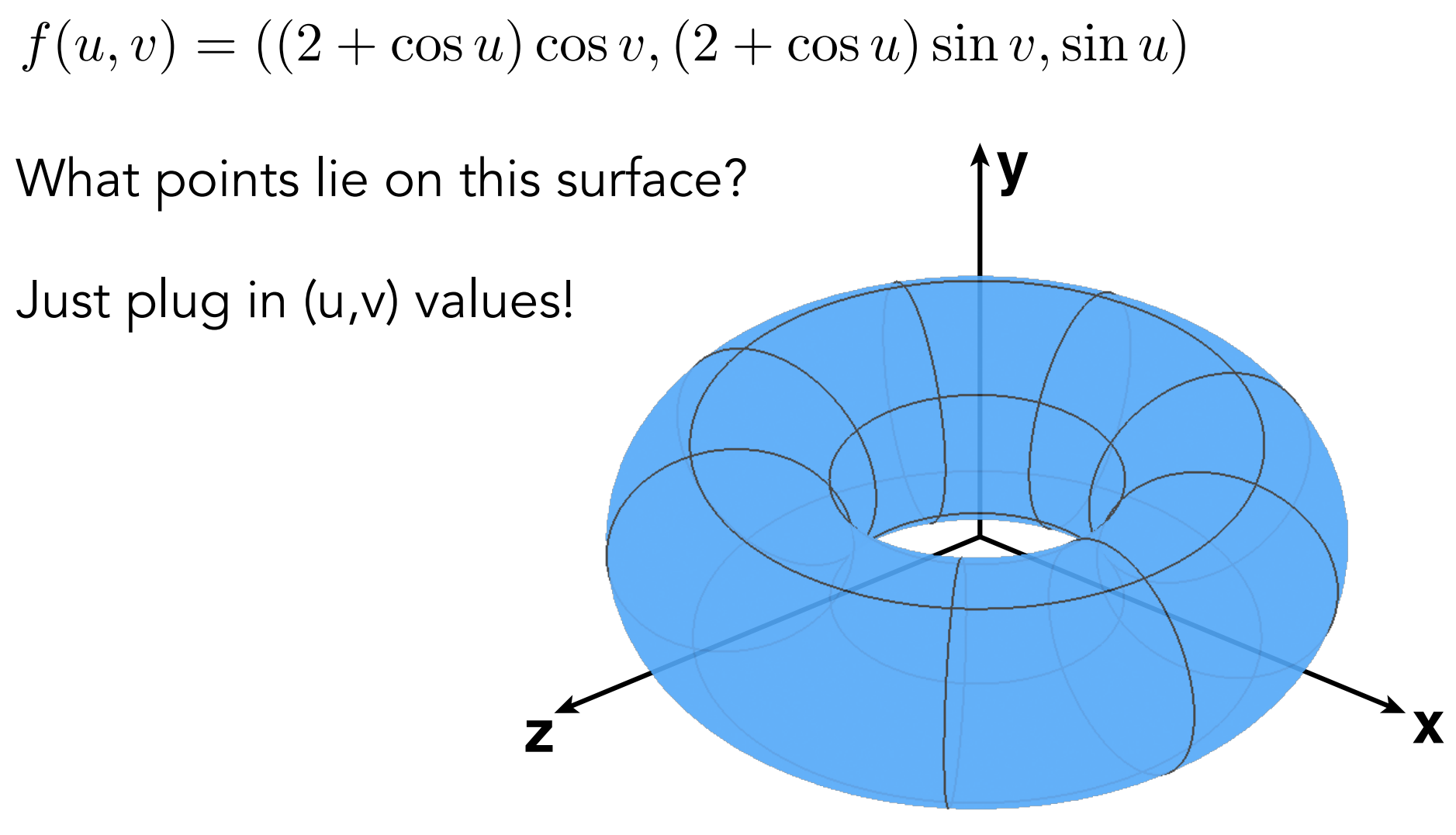
不方便判断点是否在几何体内(Inside/Outside Tests Hard)
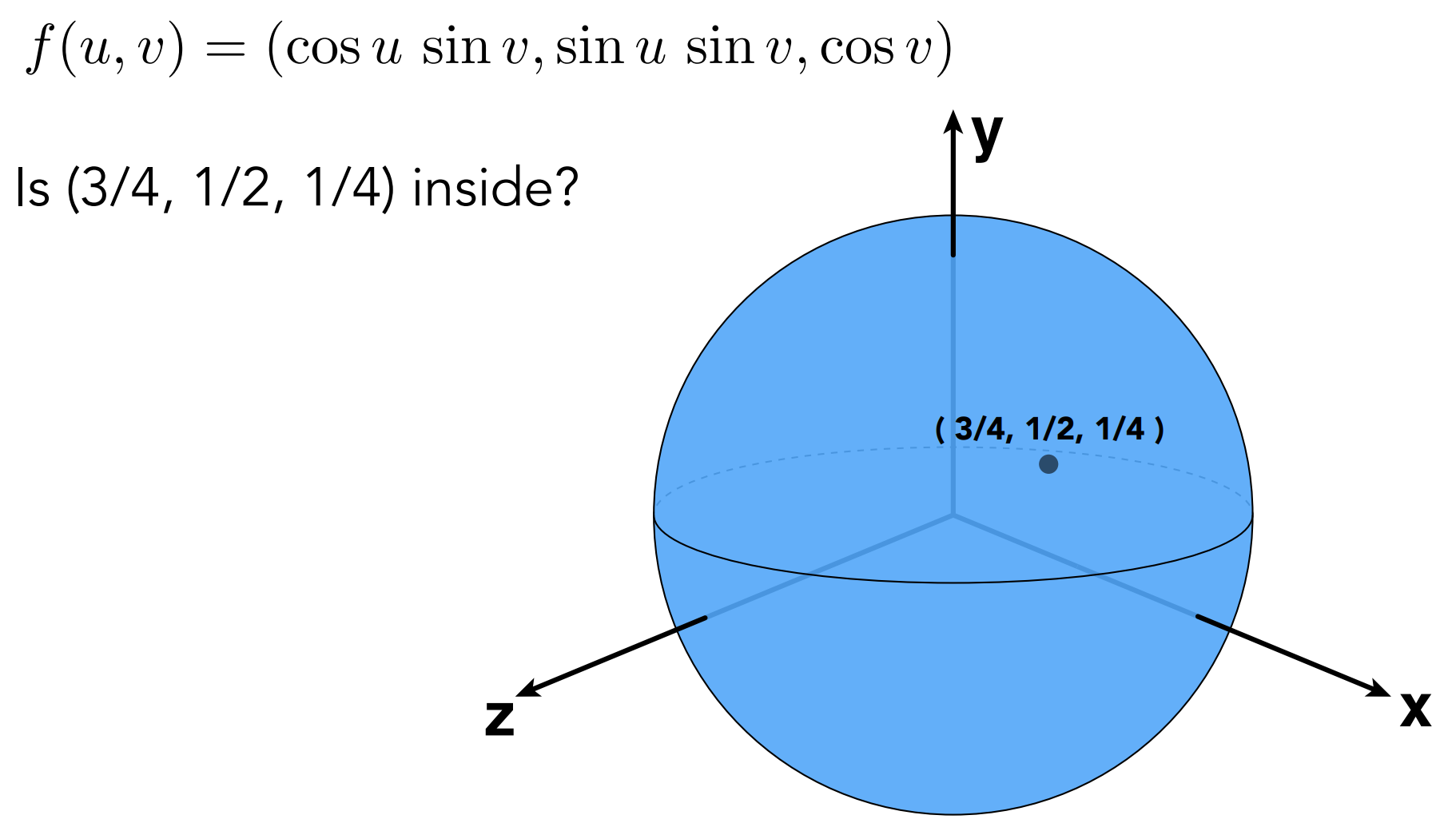
隐式、显式各有优缺点,需要根据需求选择最优的表达方式
c.1). Point Cloud

c.2). Polygon Mesh

- 常用的PolygonMesh文件,Wavefront Object File (.obj)
- v:顶点位置;vt:纹理位置;vn:normal;f:face,顶点索引/纹理索引/法线索引

c.3). Bézier Curve(贝塞尔曲线)
- 通过点$p_0$ 、$p_1$,且在这两点切线为$t0$、$t1$(切线前带系数,对于三次贝塞尔曲线系数为3)
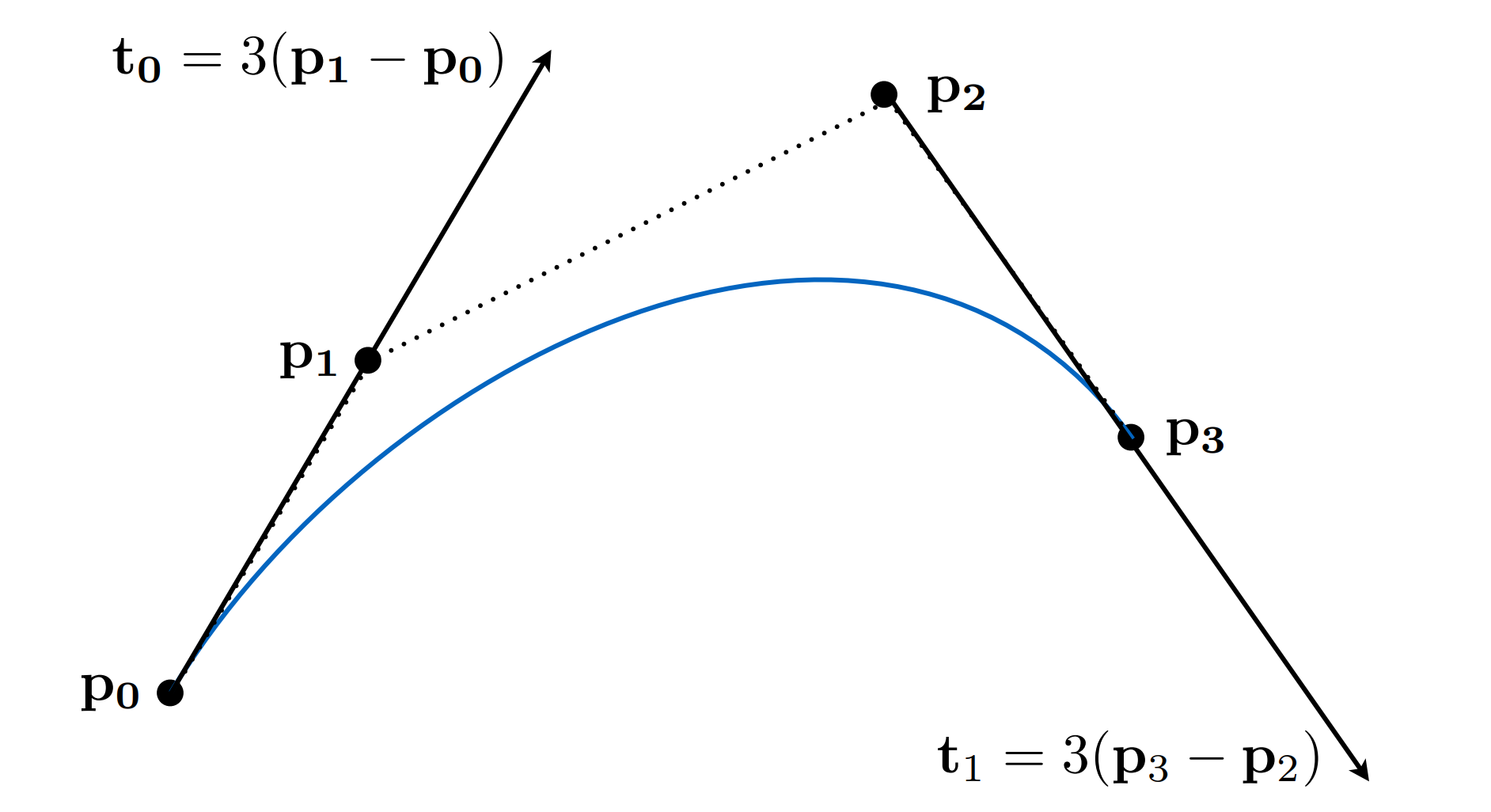
c.3.1). 计算贝塞尔曲线(德卡斯特里奥算法, De Casteljau’s Algorithm)
- 二次贝塞尔曲线
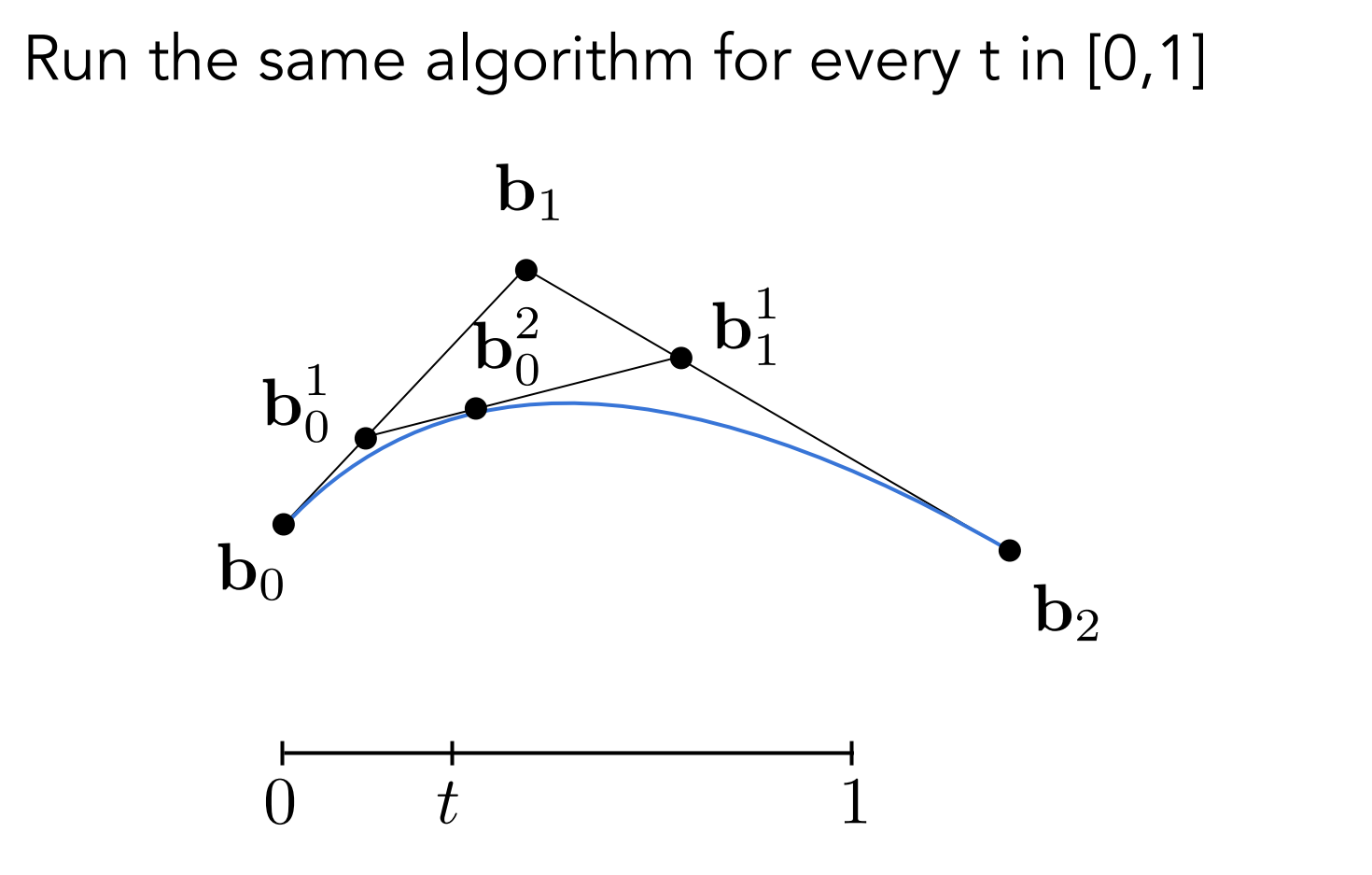
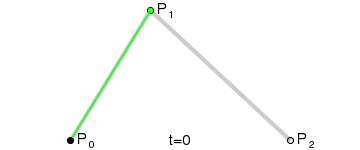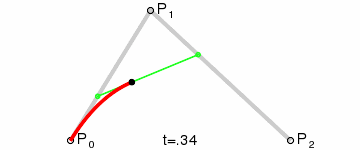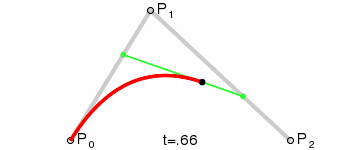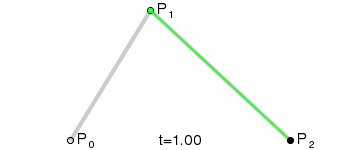
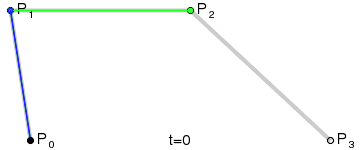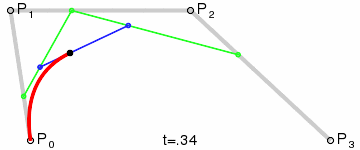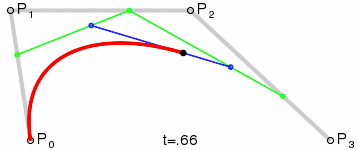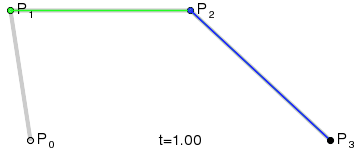
三次贝塞尔曲线(Cubic Bezier Curve)
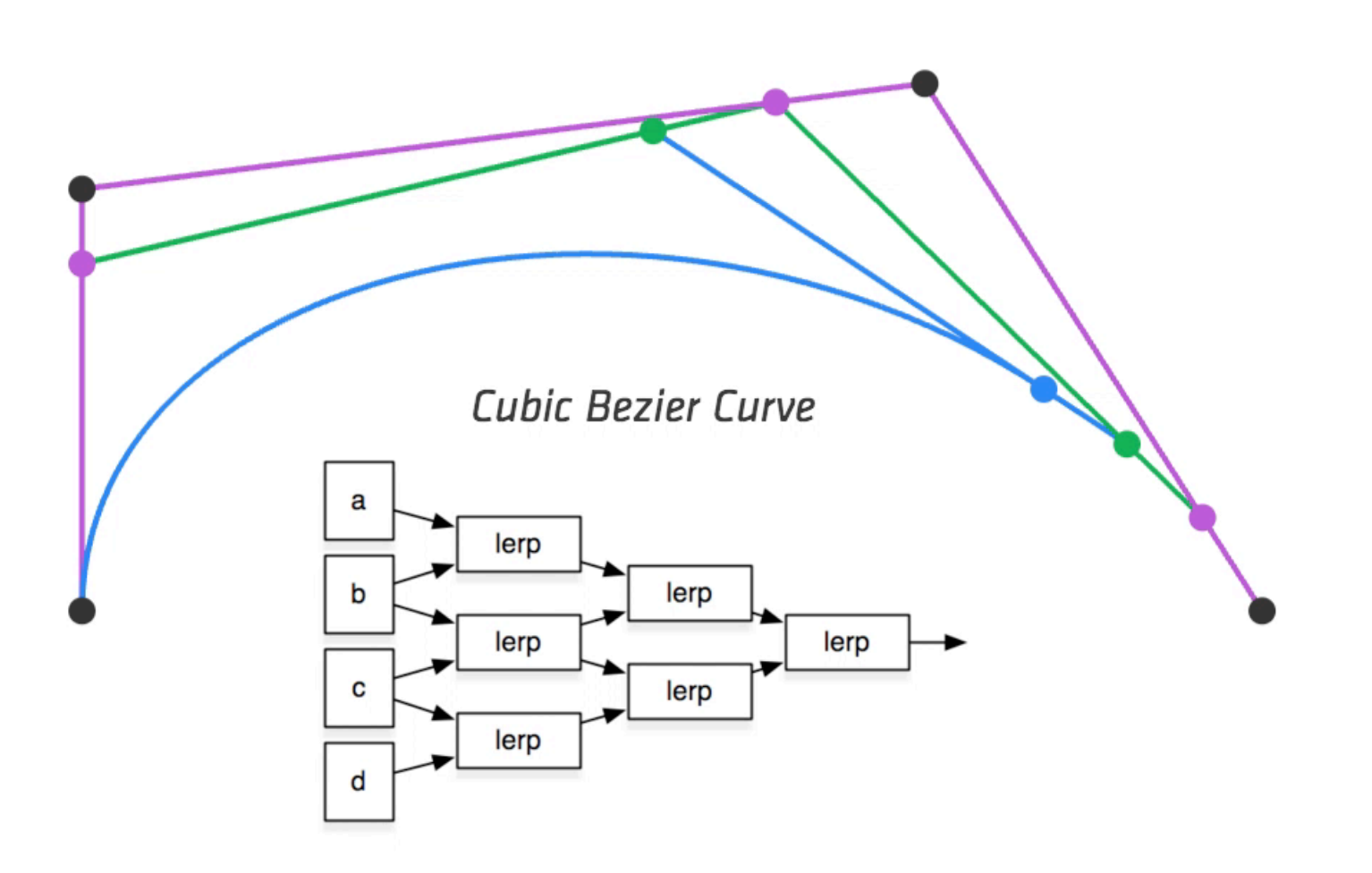
Anim:
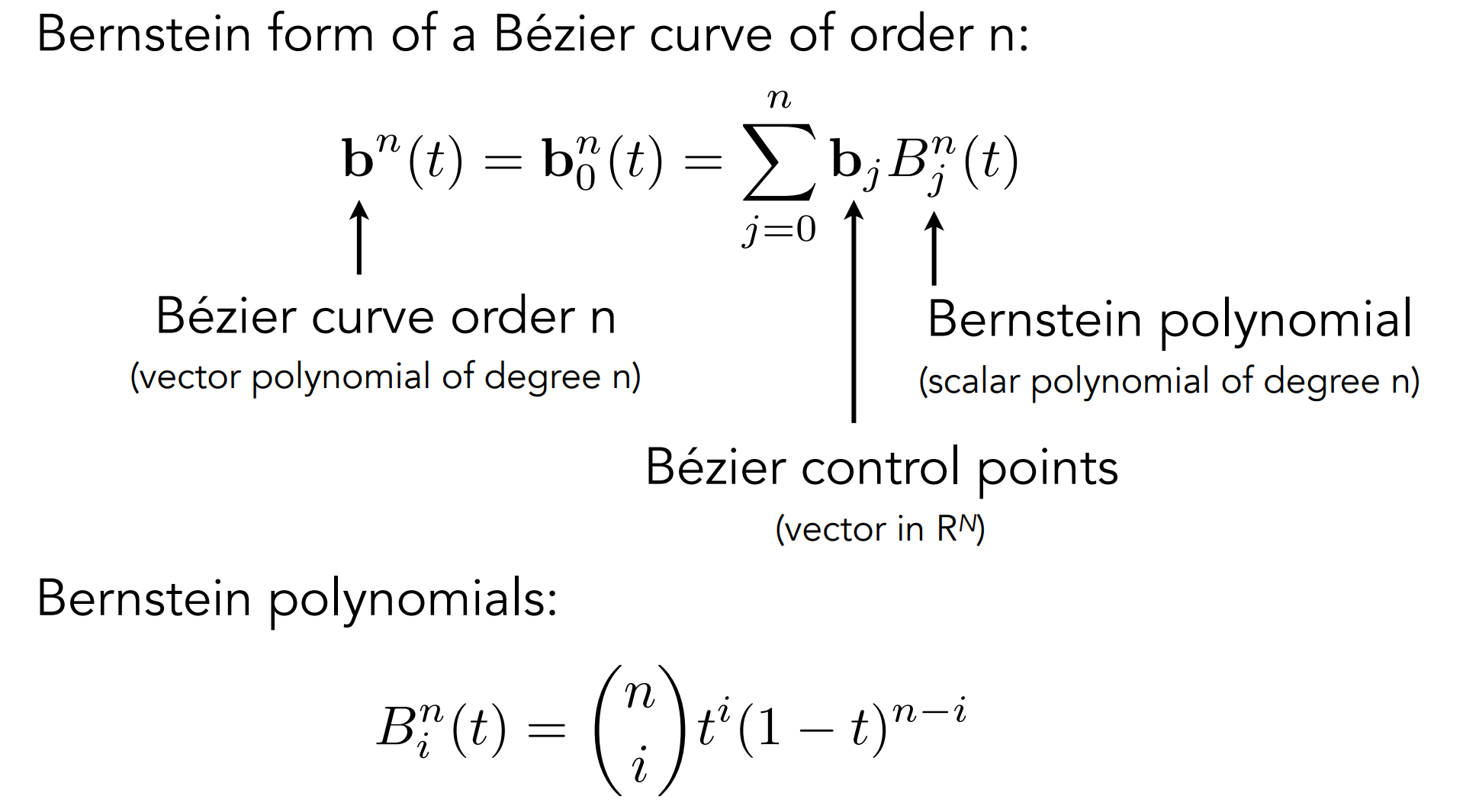
c.3.2). 代数形式
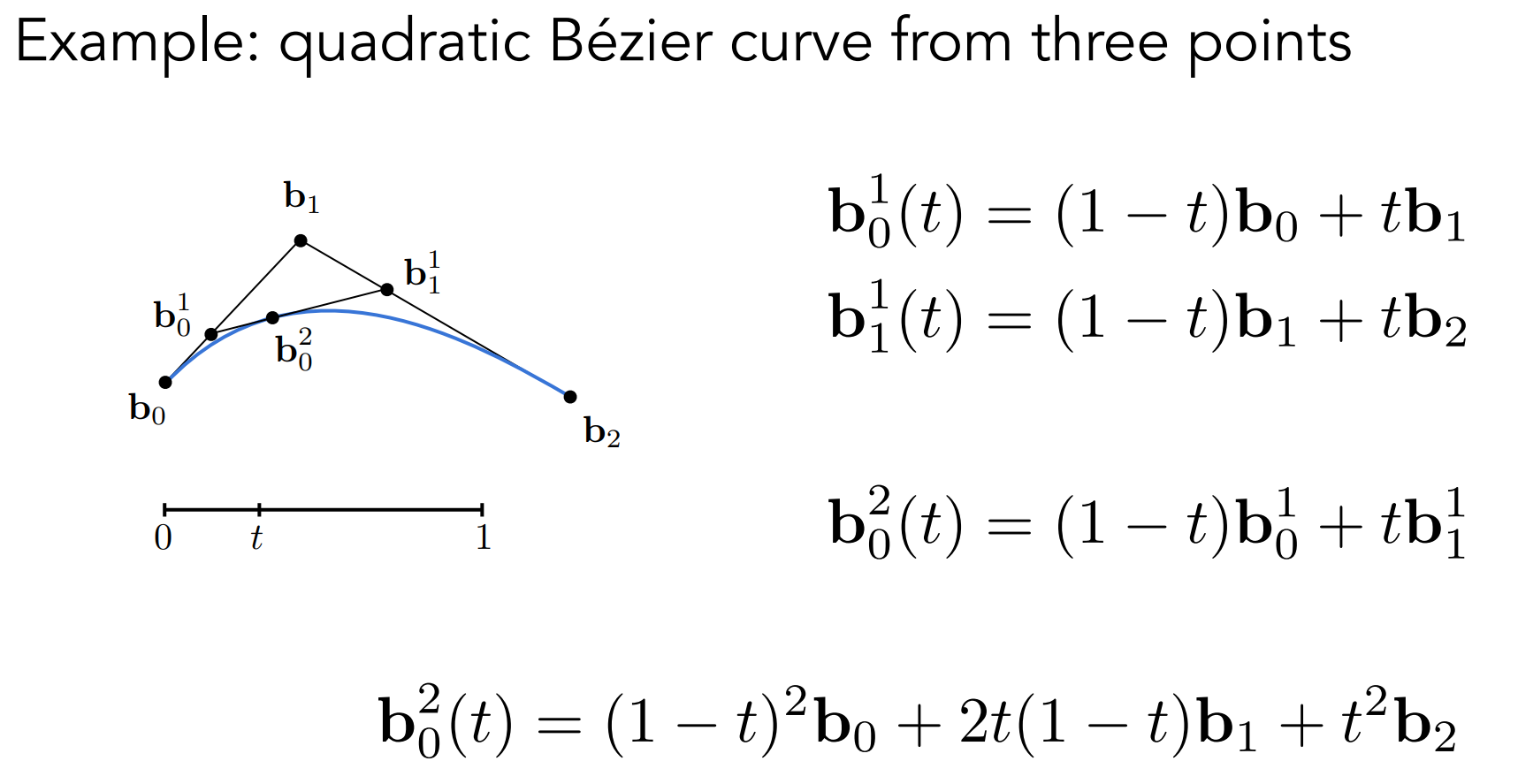
- 推出Bernstein polynomial(伯恩斯坦多项式):
C.3.3). 性质

- 即(对于三次贝塞尔曲线):
- $b_0$ 是起点,$b_3$是终点;
- 切线为$\mathbf{b}^{\prime}(0)=3\left(\mathbf{b}_{1}-\mathbf{b}_{0}\right) ; \quad \mathbf{b}^{\prime}(1)=3\left(\mathbf{b}_{3}-\mathbf{b}_{2}\right)$ (切线前带系数,对于三次贝塞尔曲线系数为3,通过求导可得)
- 仿射不变性(对于贝塞尔曲线做仿射变换,只需要对控制点进行变换)
- 凸包性质;
c.3.4). Piecewise Bézier Curves(分段贝塞尔曲线)
- 使用原因:解决高阶贝塞尔曲线控制点过多的问题;
- 分段贝塞尔曲线,常是分段立方贝塞尔(Piecewise cubic Bézier),即每一个曲线存在4个控制点;

c.3.4.1). 连续性
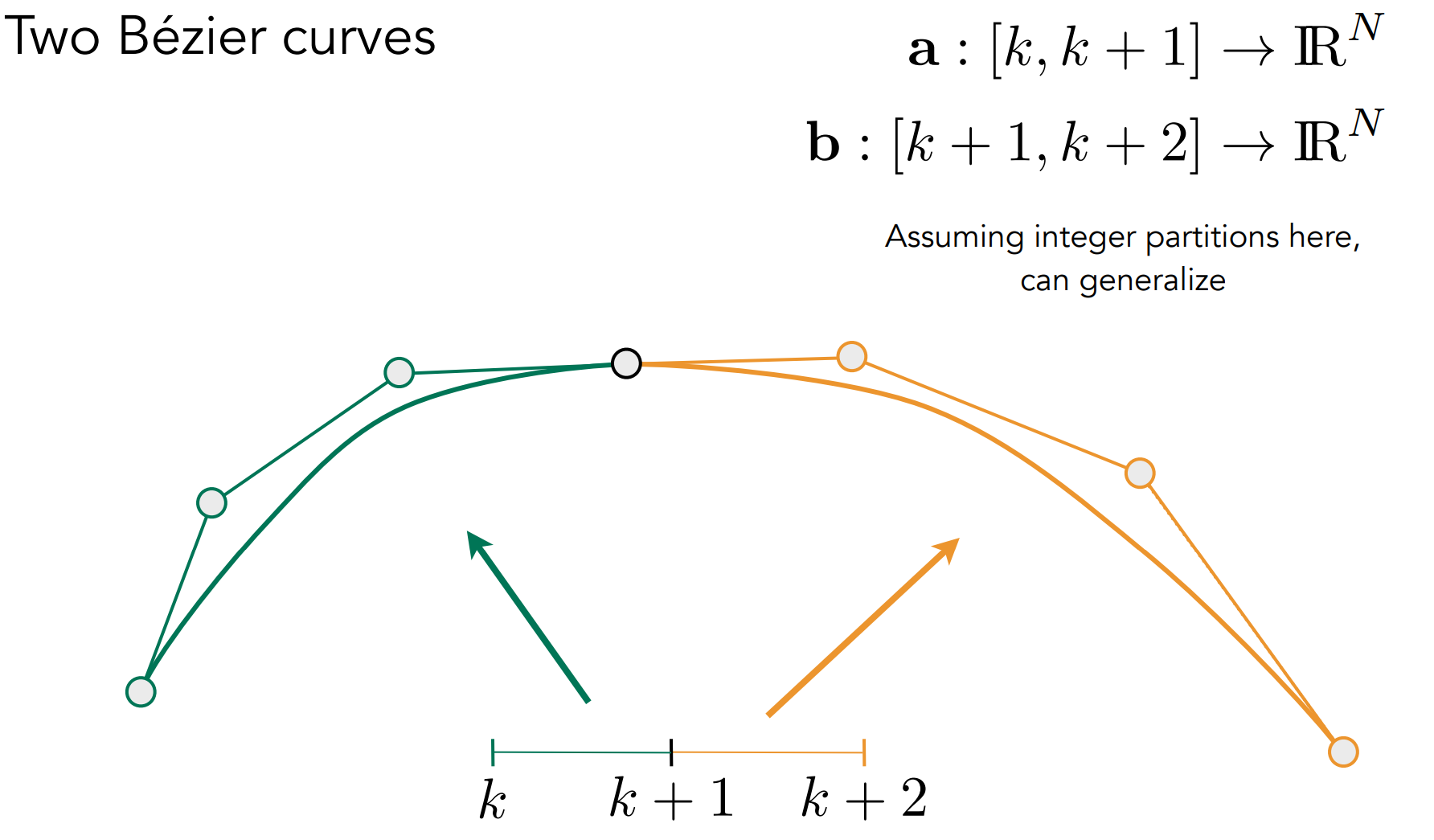
C0 连续(C表示Continuity),几何连续:$a_n=b_0$ ;
- 首尾相接,夹角任意;
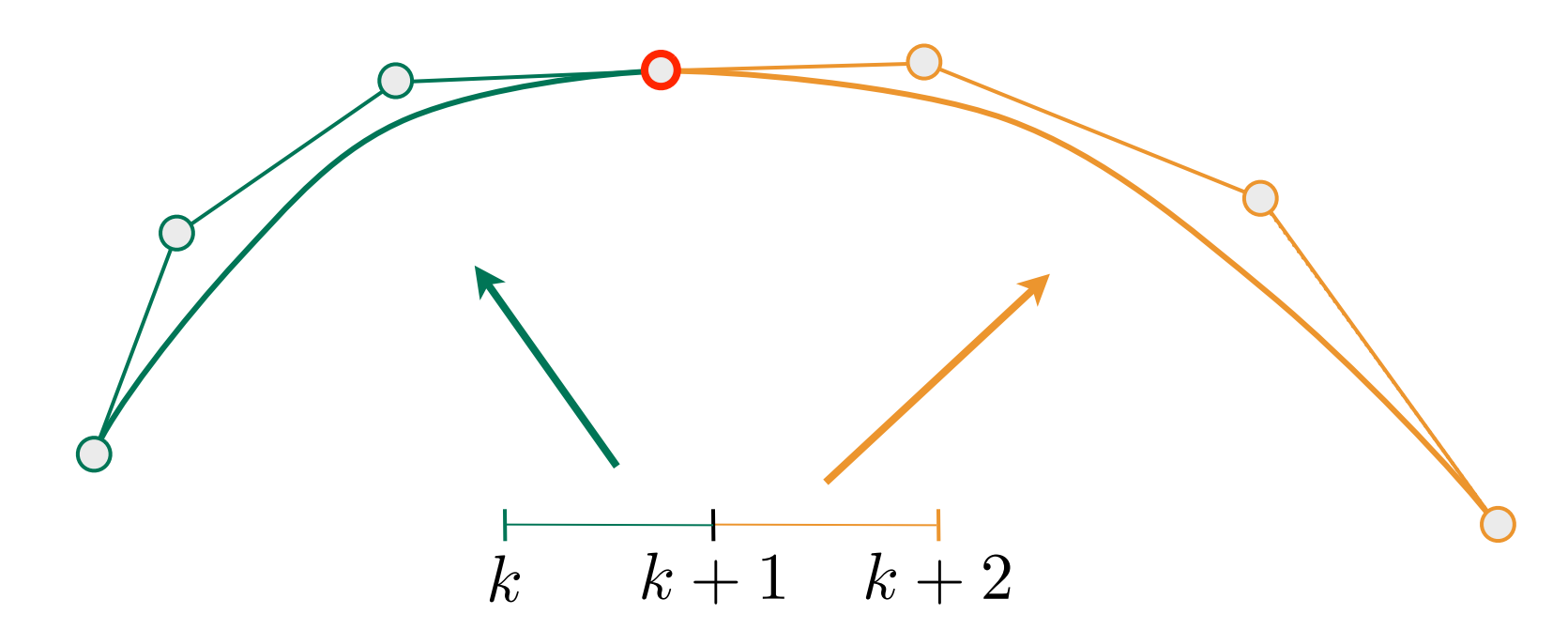
- 首尾相接,夹角任意;
C1 连续,参数连续:$a_n=b_0={1\over2}(a_{n-1} + b_1)$ ;
- 切线相等,即一阶导数连续;
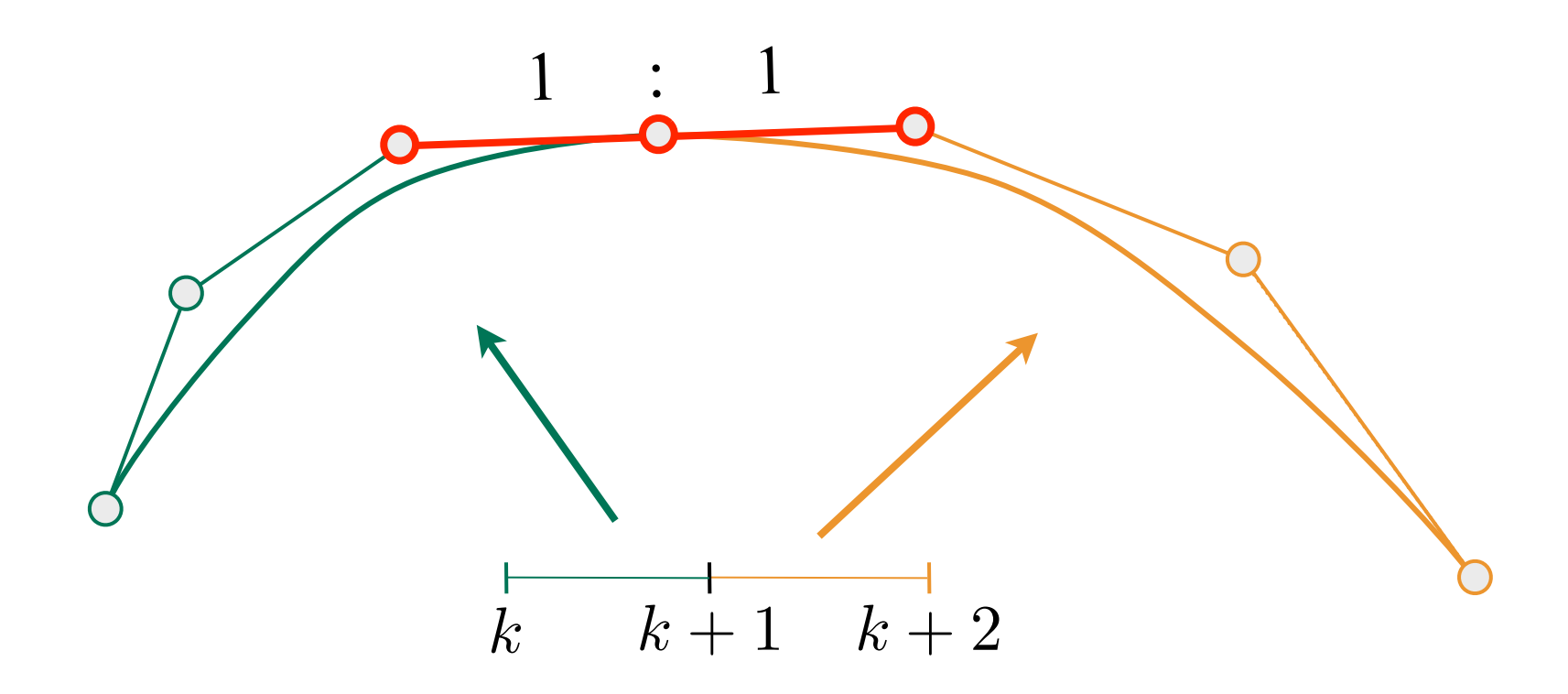
- 切线相等,即一阶导数连续;
3.5). Other types of splines(待深入)


- In this course
- We do not cover B-splines and NURBS
- We also do not cover operations on curves (e.g. increasing/decreasing orders, etc.)
- To learn more / deeper, you are welcome to refer to Prof. Shi-Min Hu’s course: https://www.bilibili.com/video/av66548502?from=search&seid=65256805876131485
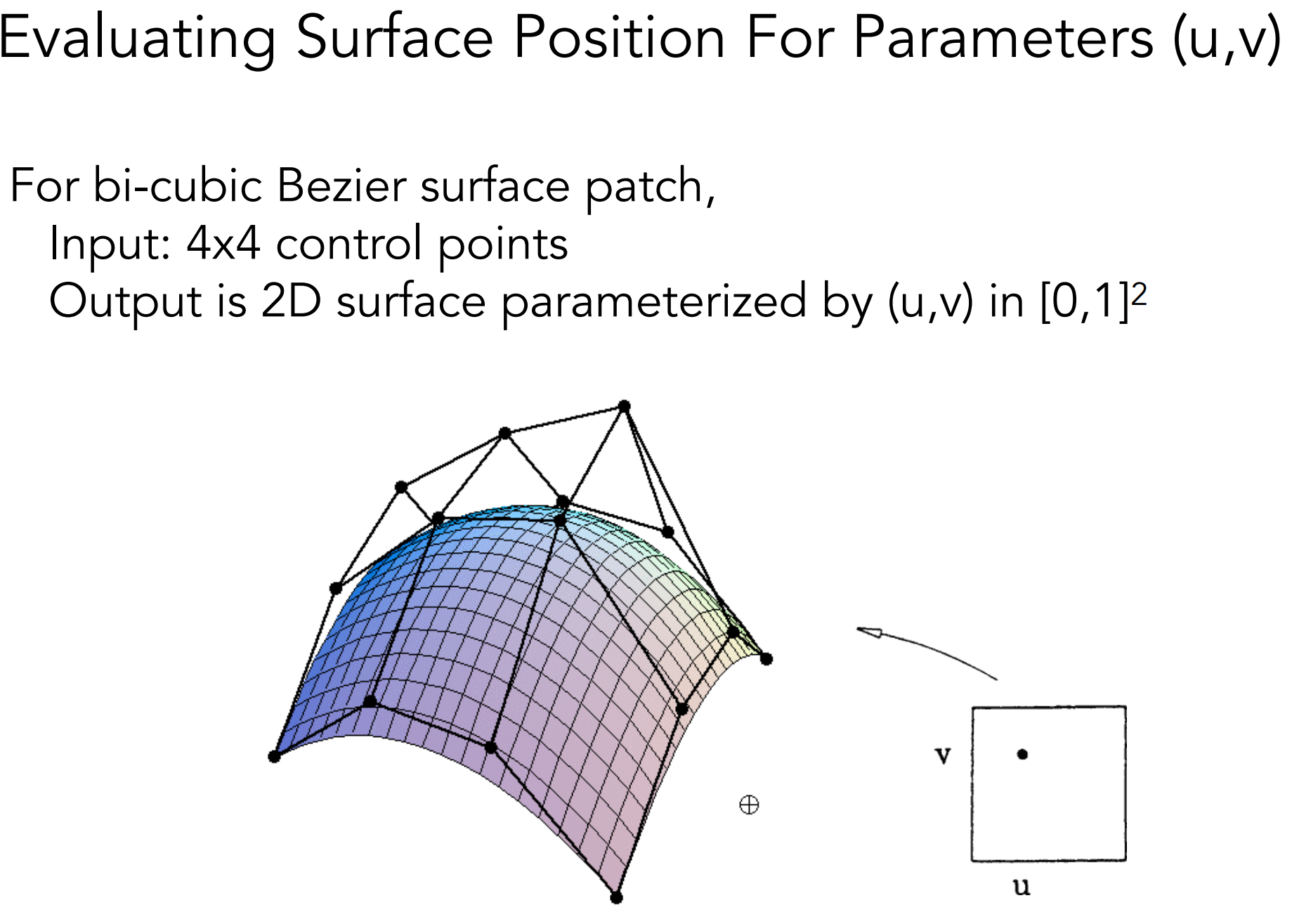
3.6). Bezier Surface
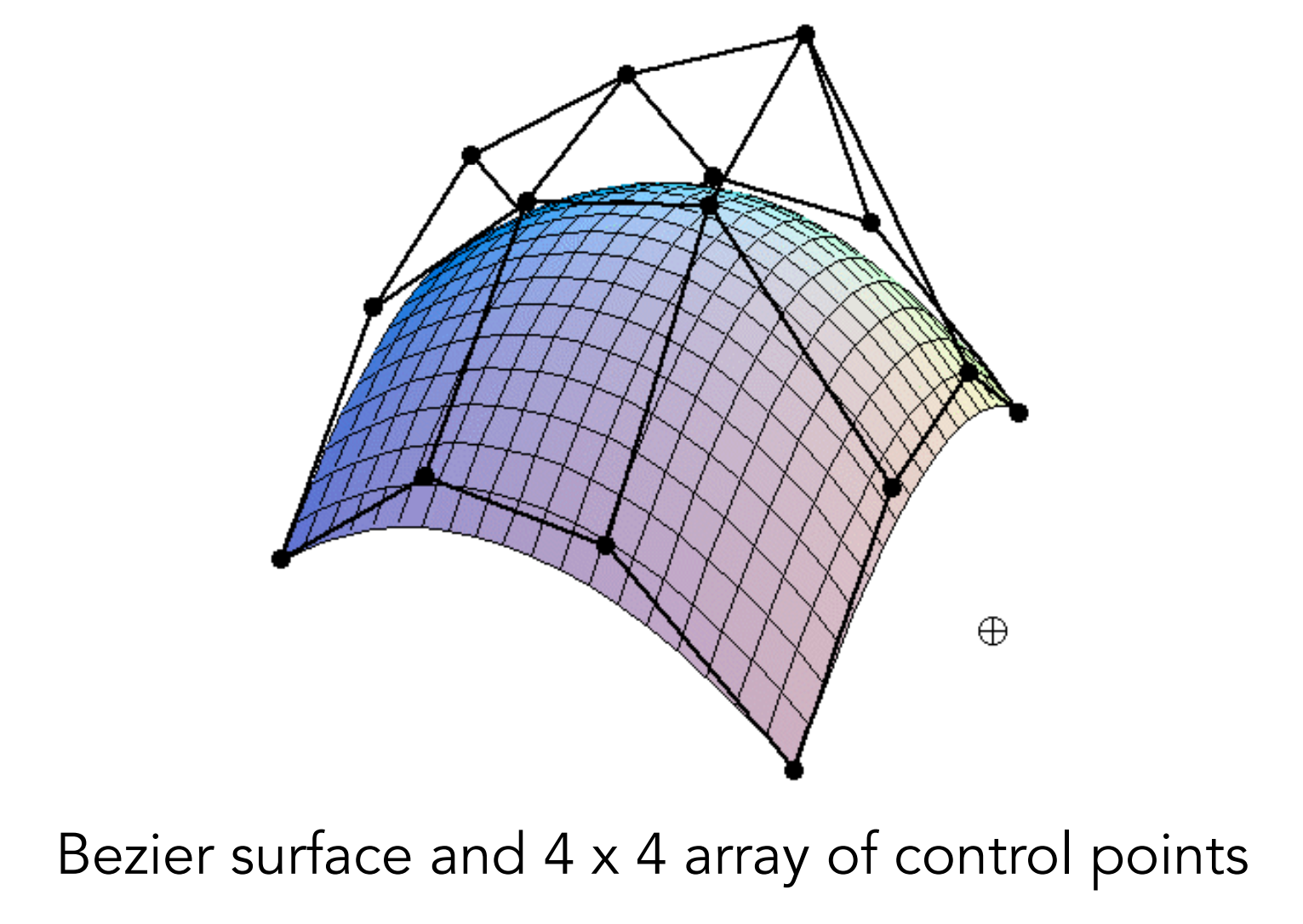
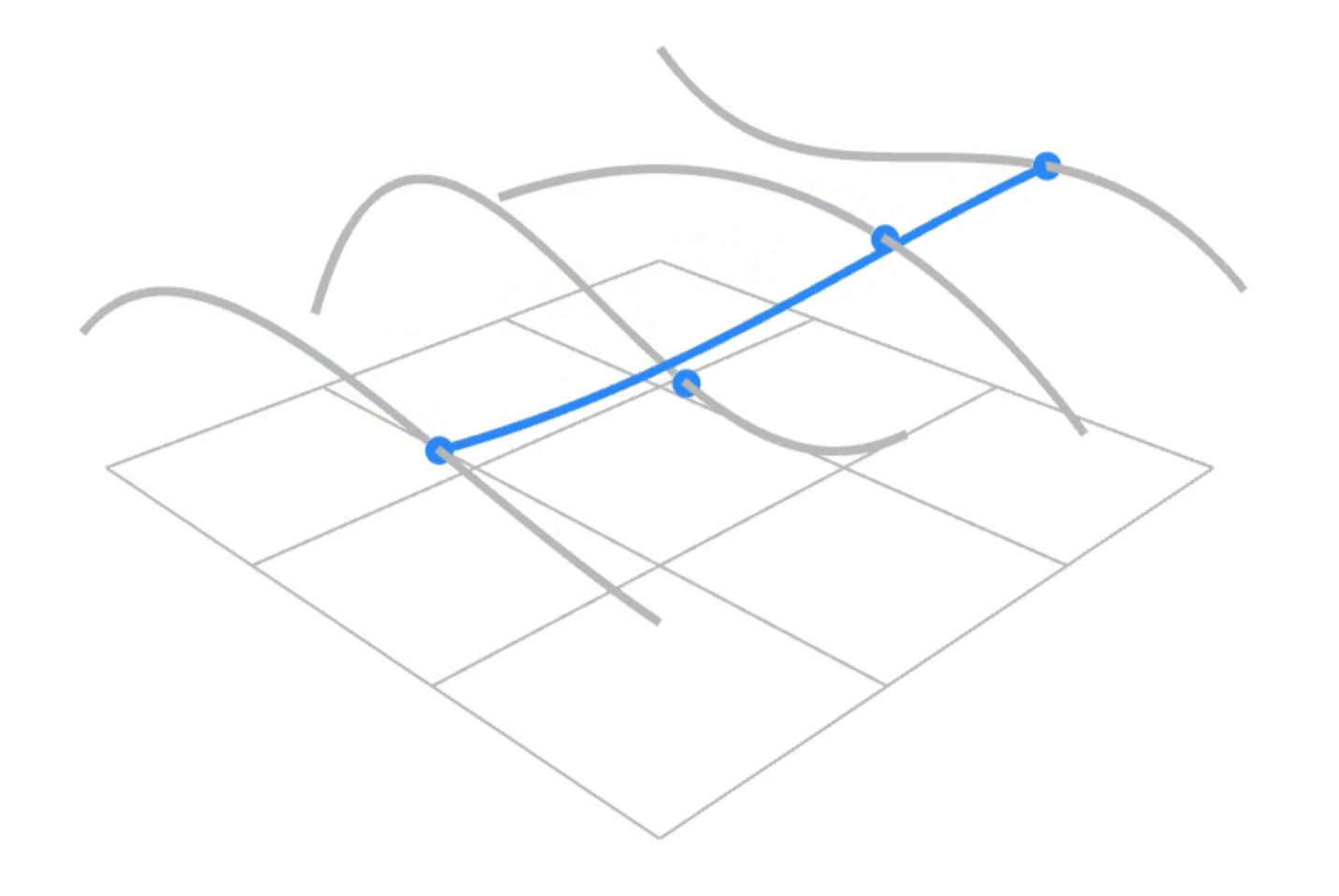
- Animation: Steven Wittens, Making Things with Maths, http://acko.net
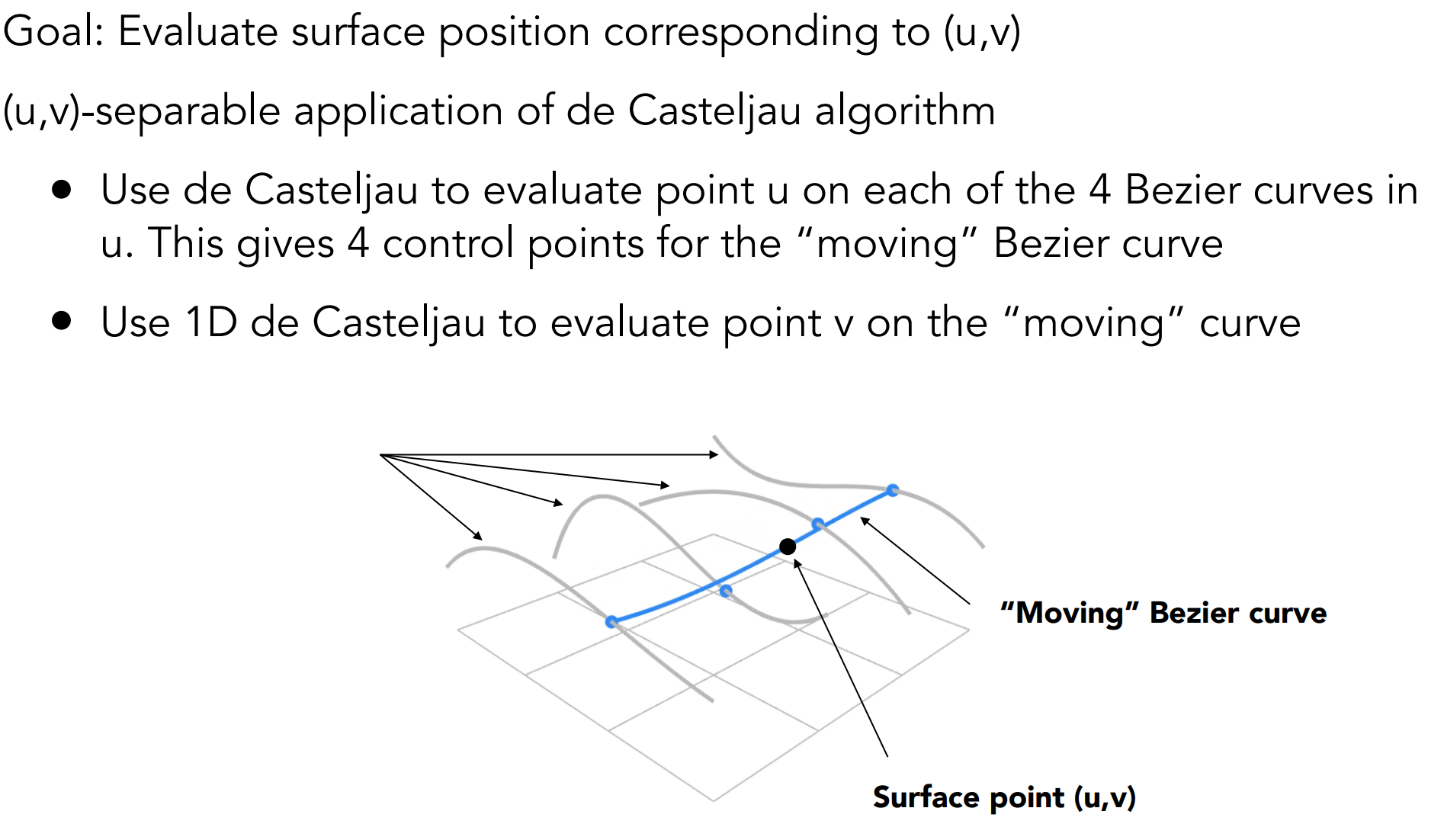
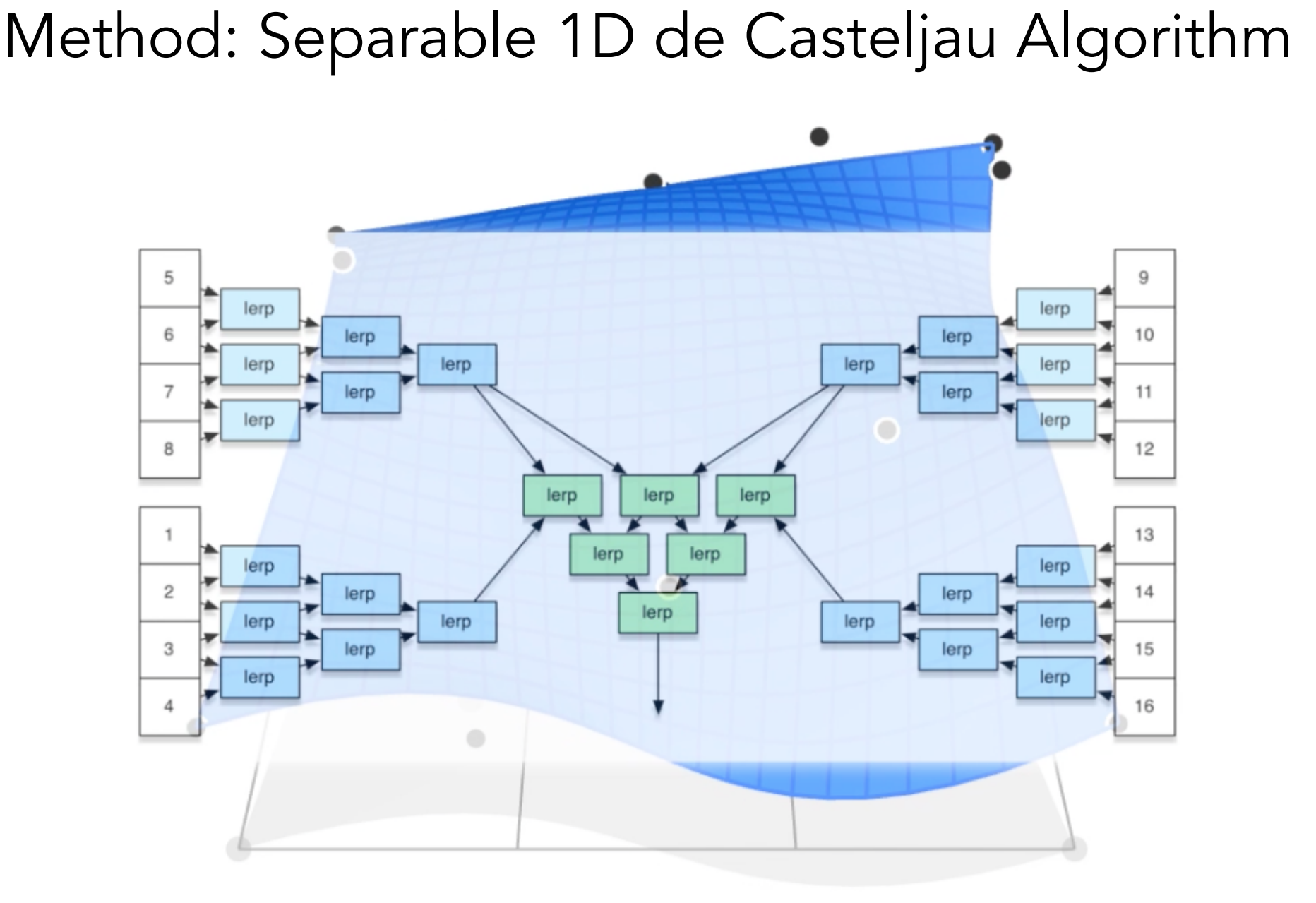
3.6.1). Evaluating Bézier Surfaces

Lecture 13 Geometry
a). Subdivision

- 以下是几种常用的细分方法:
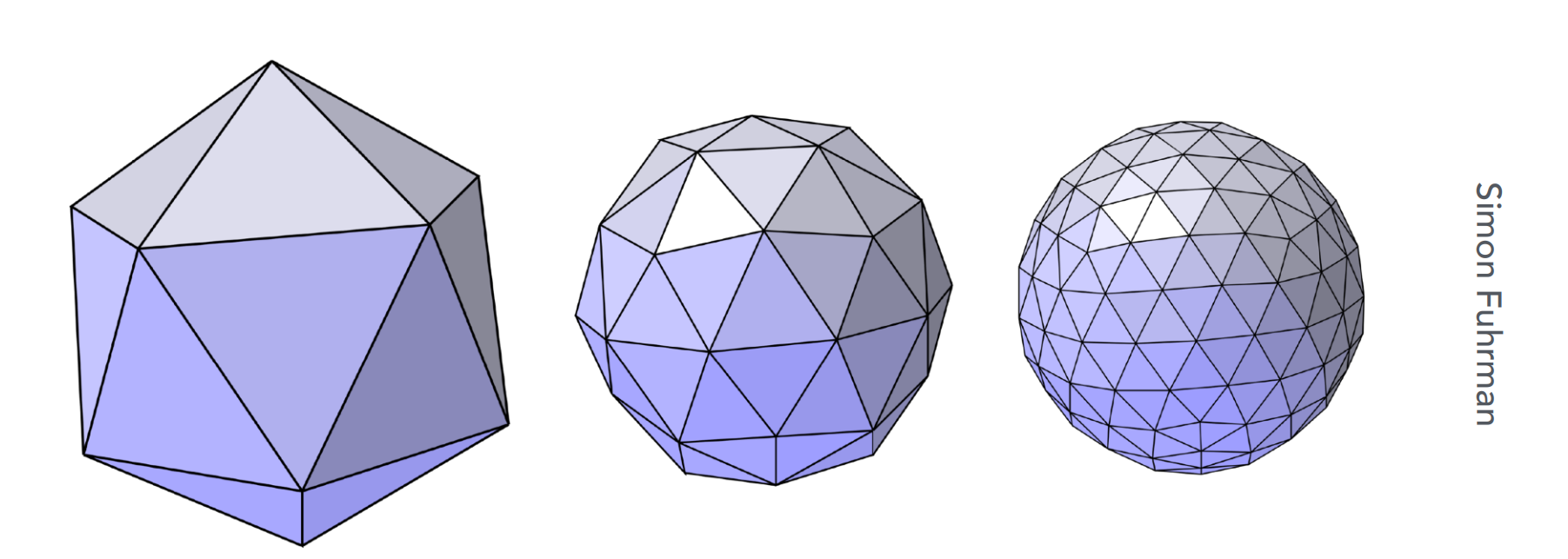
a.1). Loop Subdivision(Loop是人名)
- 细分对象:三角面
- 首先,创造更多的三角面;
- 第二,改变他们的位置;
- 具体做法:
- 将每个三角形细分为四个;
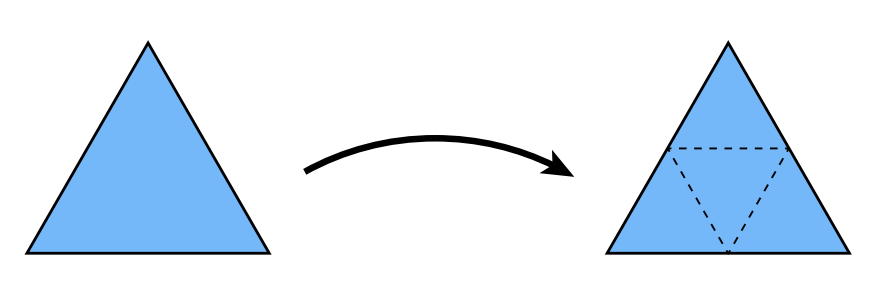
- 根据权重分配新的顶点位置;
- 区分新/老顶点,做不同变换;
- 对于新顶点:
- $P_{new} = {3\over8}(A+B)+{1\over8}(C+D)$
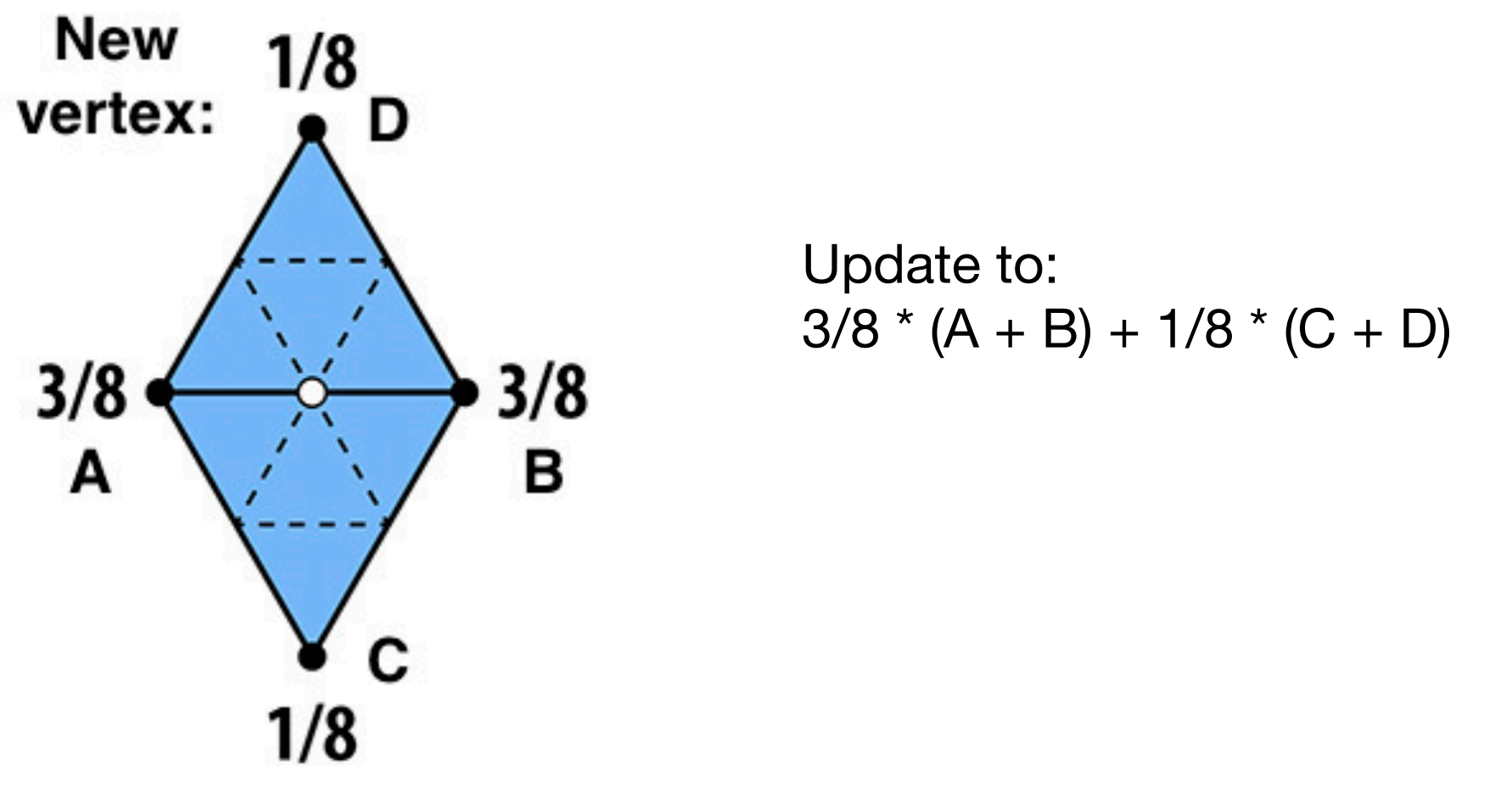
- $P_{new} = {3\over8}(A+B)+{1\over8}(C+D)$
- 对于老顶点:
- $n:$ 顶点的度(图论,与该顶点关联的边的数目,该处即为与该顶点连接的边的数量)
- $u:$ $3/16$(如果$n=3$),$3/(8n)$ (其他情况)
- $P_{new} = (1-nu)original_position + u·neighbor_position_sum$
- 将每个三角形细分为四个;
Loop Subdivision Results:
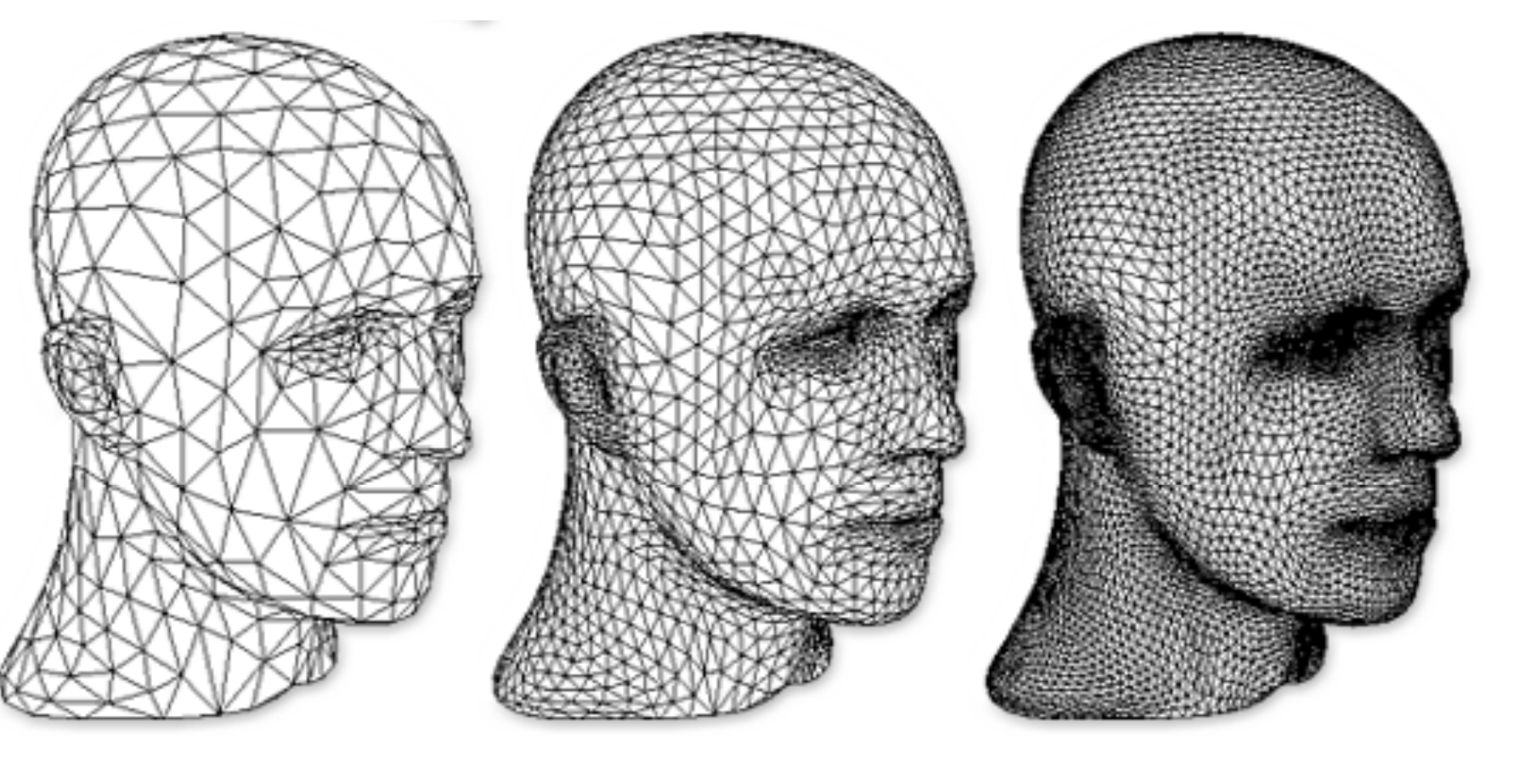
缺点:Loop只能处理三角面;
a.2). Catmull-Clark Subdivision
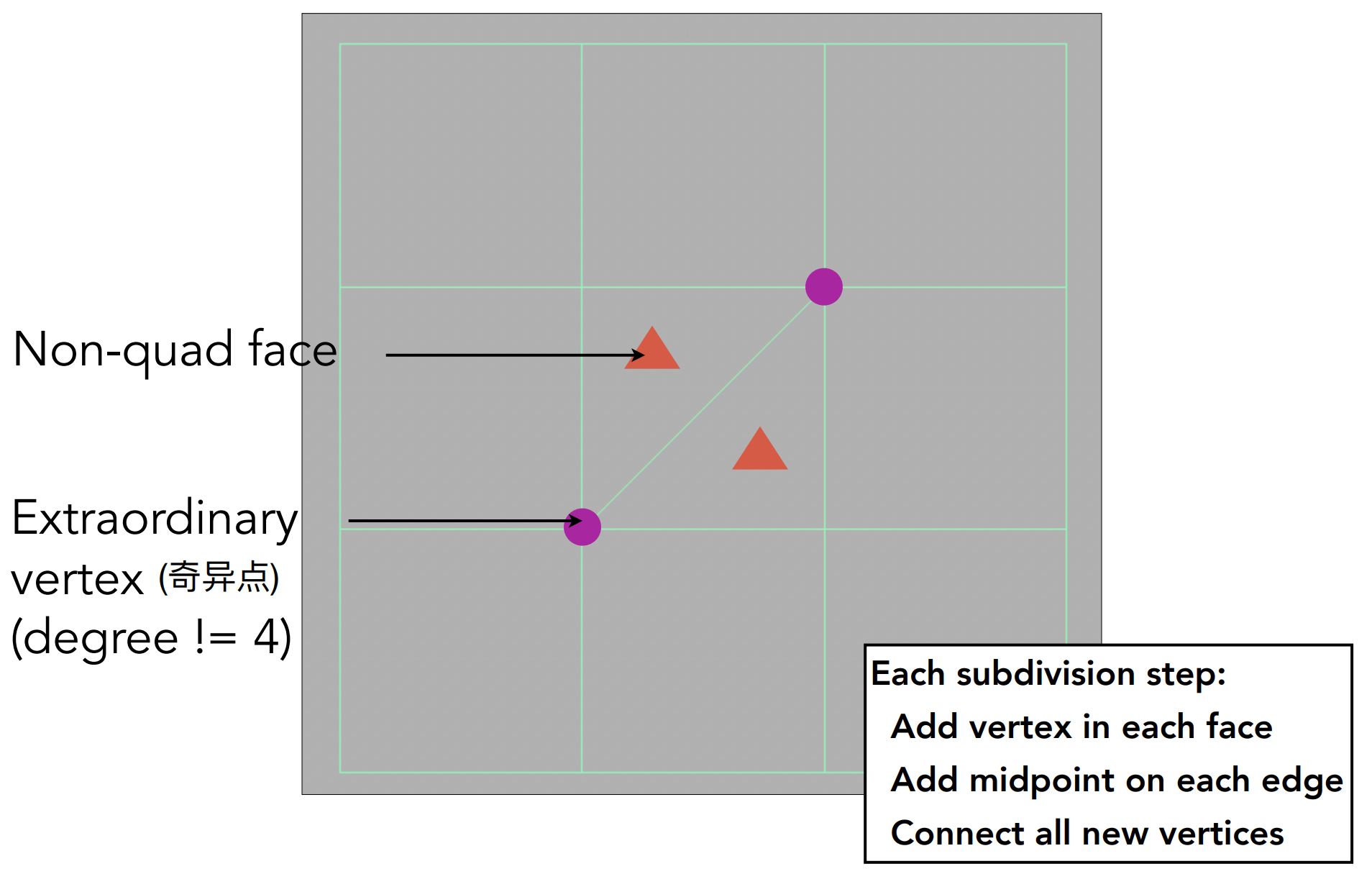
概念:
- 奇异点(Extraorinary vertex):度不为4的点;
具体过程:
第一次细分:
- 每条边取中点,每个面也取其中一点;
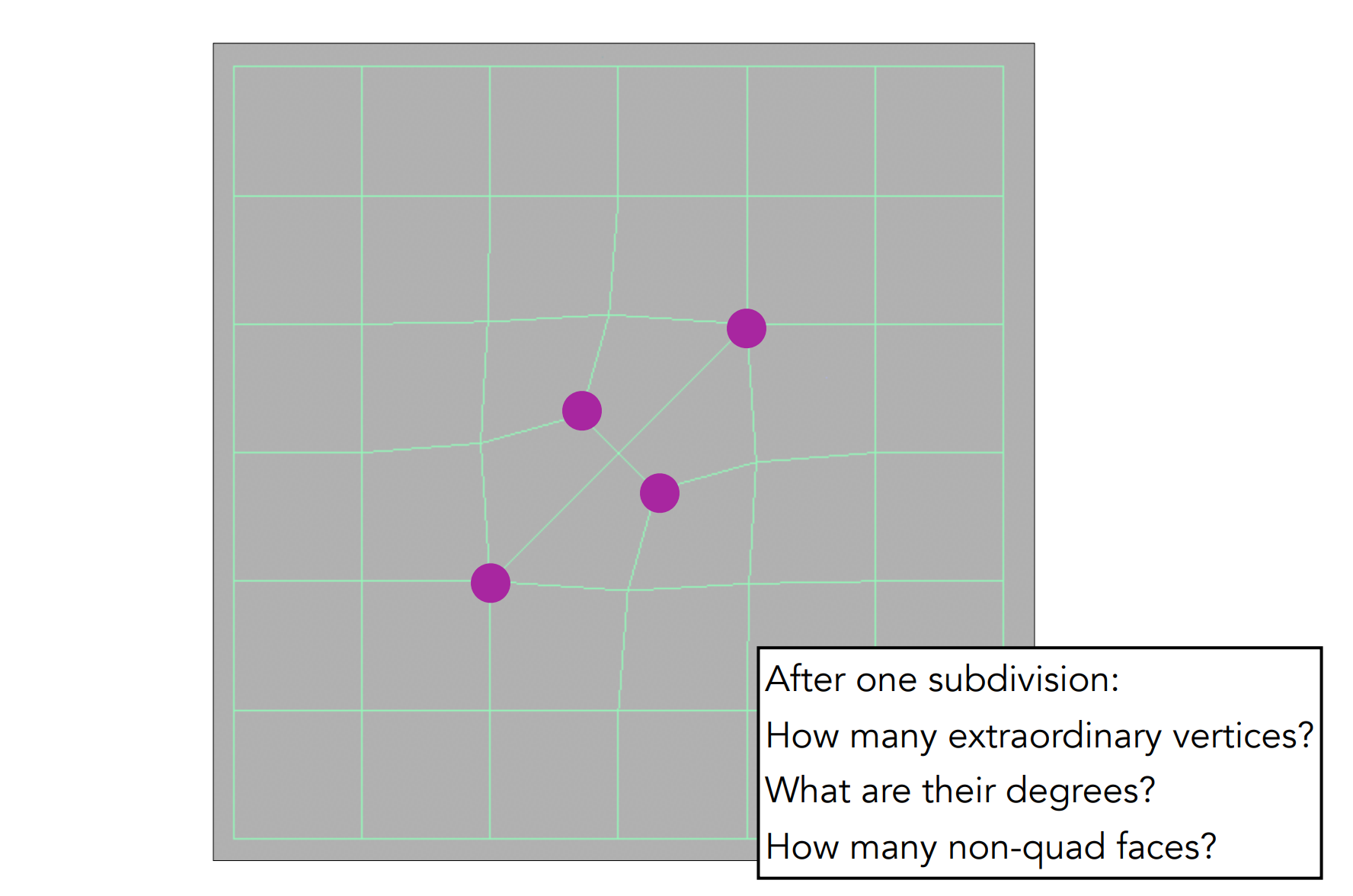
- 第一次细分后,引入(n个,n=非四边形数目)奇异点,非四边形面消失。之后,奇异点不在增加,因此,之后细分只针对四边面;
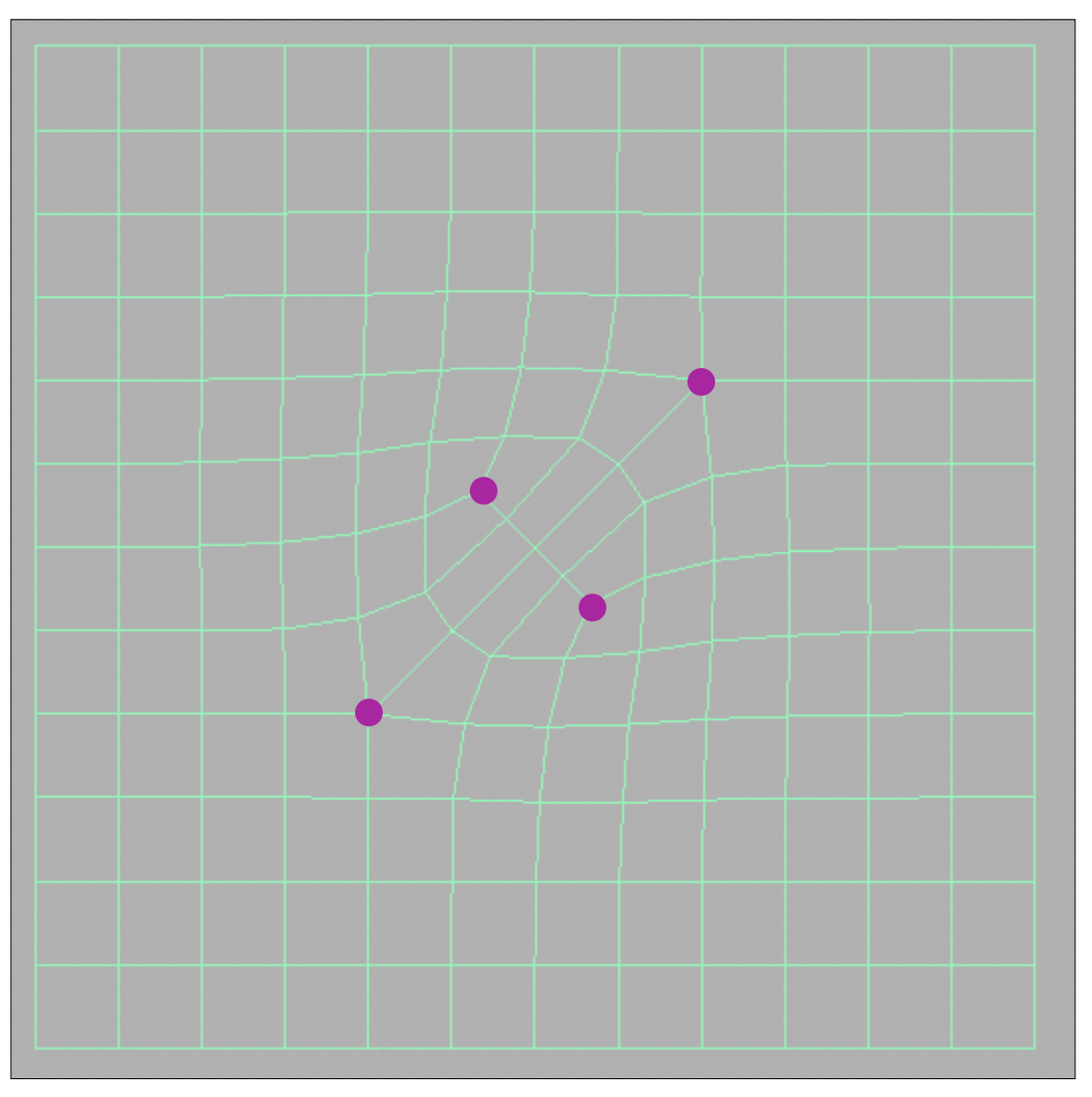
- 每条边取中点,每个面也取其中一点;
Catmull-Clark Vertex Update Rules (Quad Mesh)

- Face point:
$$
f=