Games101-13-16 RayTracing

Lecture 13 Ray Tracing

a). vs. Rasterization

• 光栅化难以表现全局（global）效果，如

  • （软）阴影（Soft shadows）
  • 光线反弹超过一次（Glossy reflection）
  • Indirect illumination（间接光照）

  

• Rasterization is fast, but quality is relatively low；

b.). Basic Ray-Tracing Algorithm

• 光追中光线的性质：

  1. 光是沿直线传播的；
  2. 光相交时，并不产生干扰；
  3. 光从光源出发，传播到眼睛（由于光路可逆，也可是光线从眼睛出发，传播到光源）

  

b.1). Ray Casting

• 做法：

  1. Generate an image by casting one ray per pixel;（生成从眼睛出发的光线）
  2. Check for shadows by sending a ray to the light;（检查光线投射点是否可传播到光源）
• 
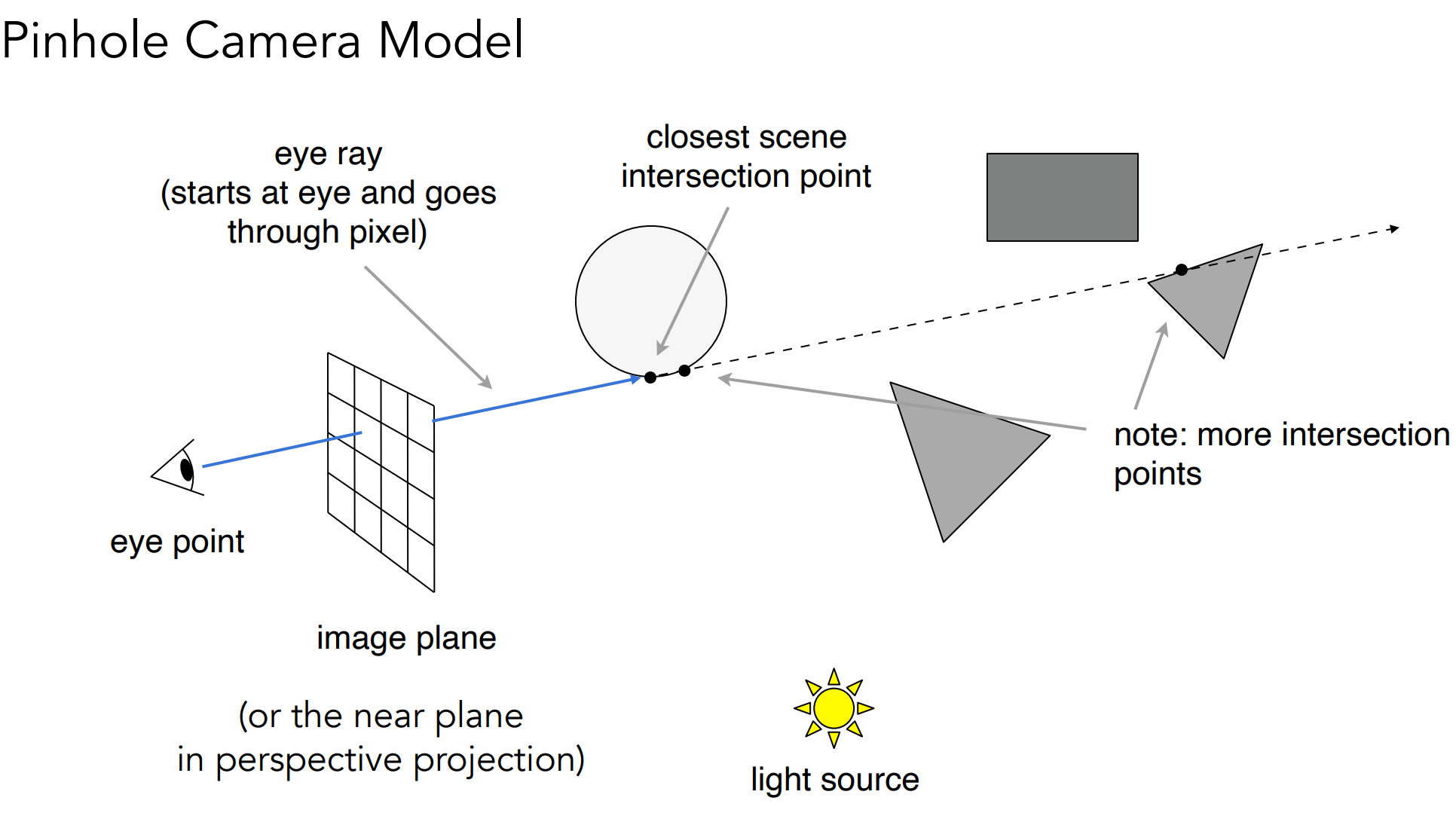
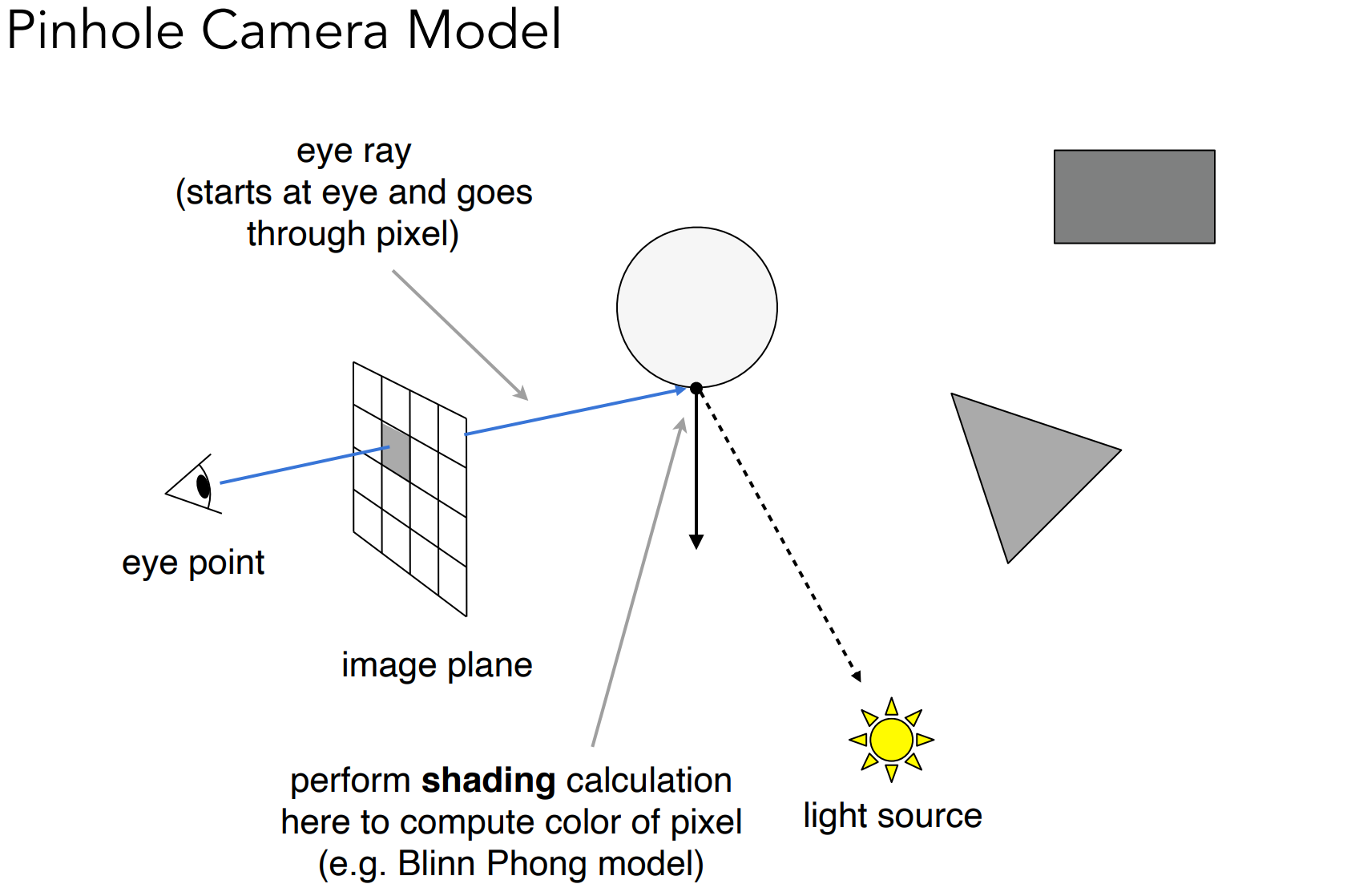
  • 光线由眼睛出发，可不再使用深度缓存；
  • 投射点到光源发射Shadow Ray，查看该点是否在阴影里（是否对光源可见）；

c). Whitted-Style Ray Tracing(Recursive, 递归)

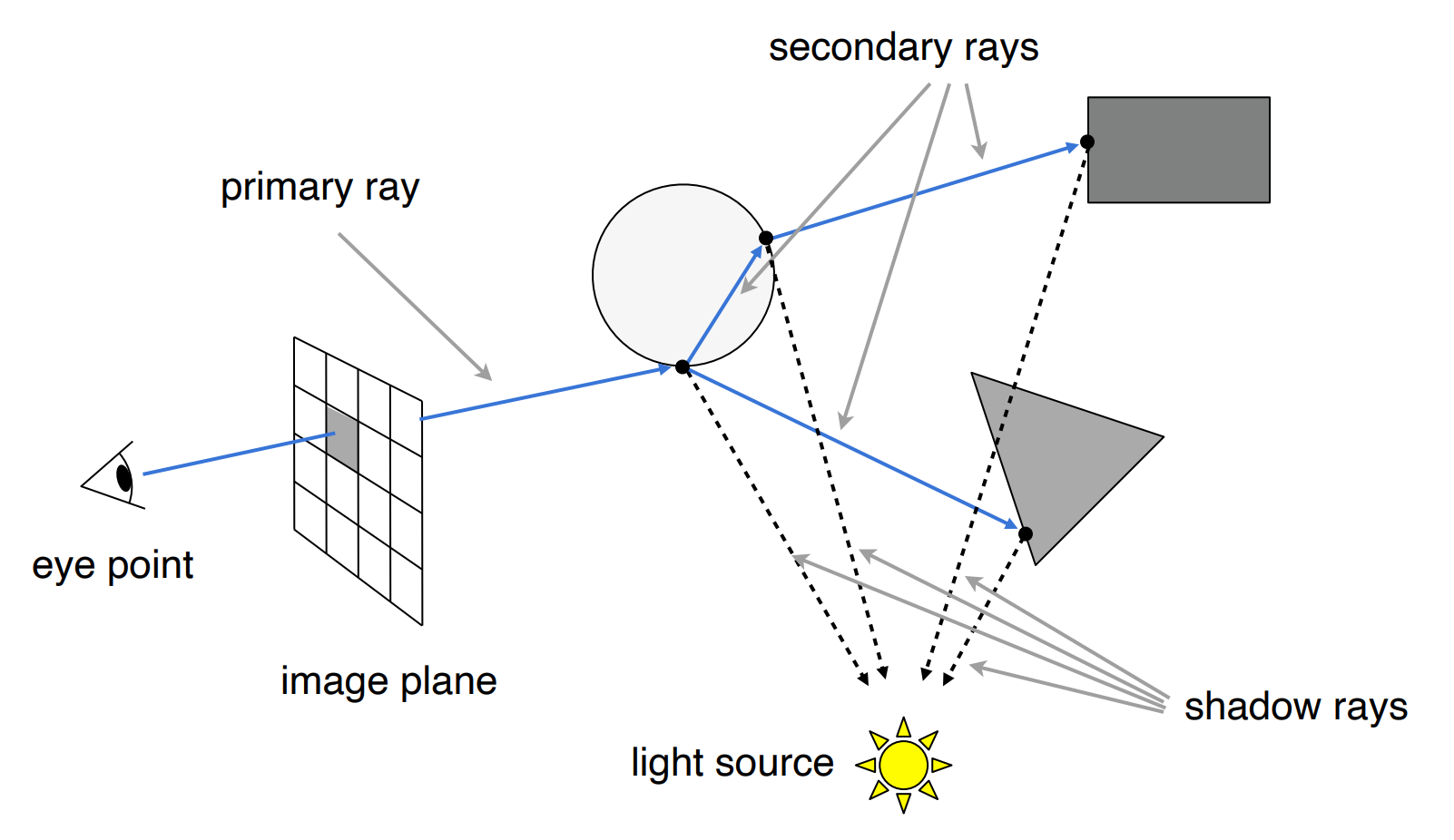
• 过程：
  • 生成眼睛到像素a的光线（Primary ray），打到第一个与光线相交的点；
  • 形成反射（镜面反射）和折射的光线（Secondary rays，之后的都是Secondary rays）；
  • 对每条光线与object的交点做到光源的光线（Shadow rays）；
  • 将所有Shadow rays未被阻挡的光线的着色结果相加，即为像素a的着色结果；

c.1). Ray-Surface Intersection（求交点）

c.1.1). 与球形相交：

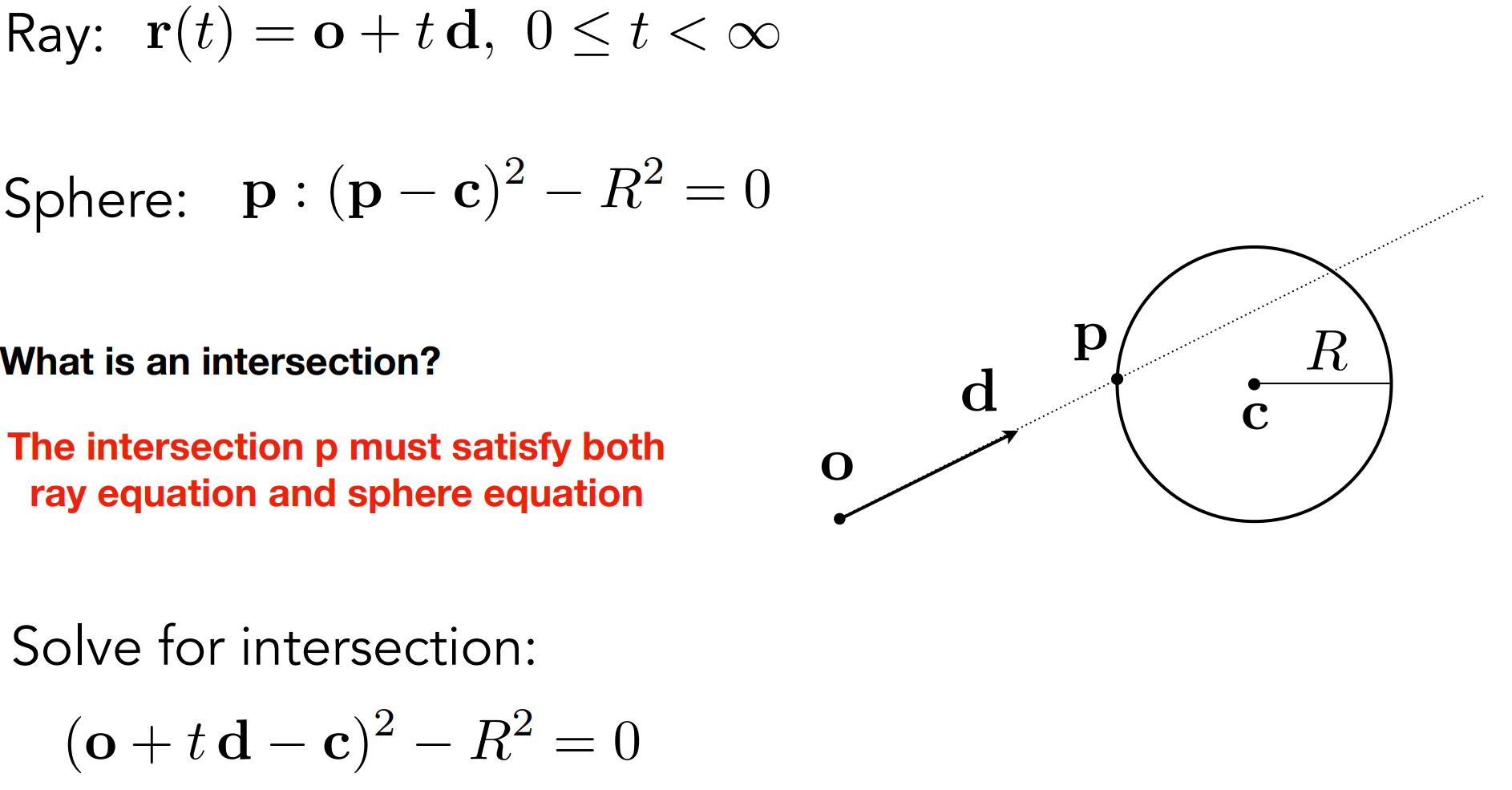
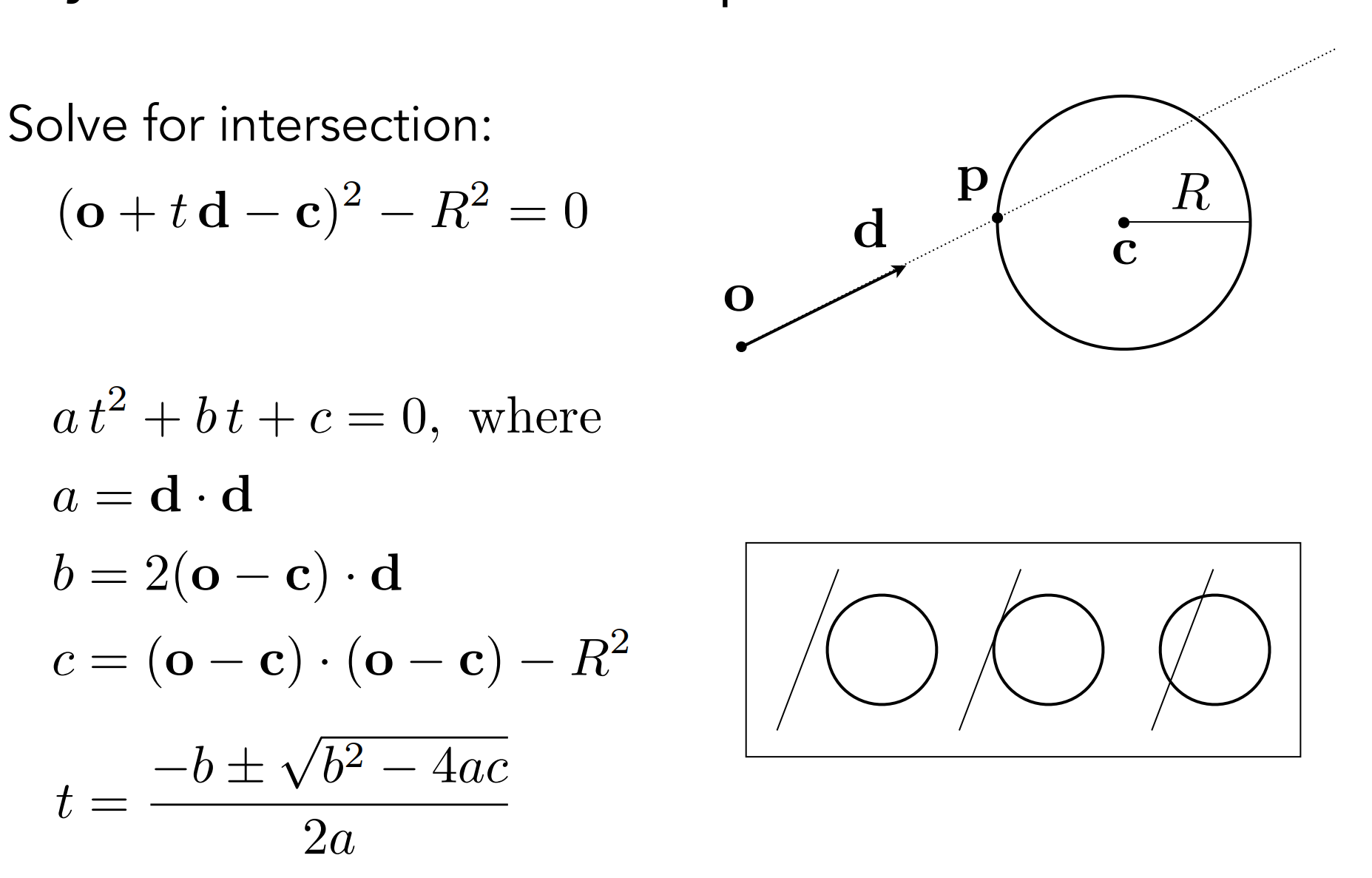
• 推广：与隐式表面相交

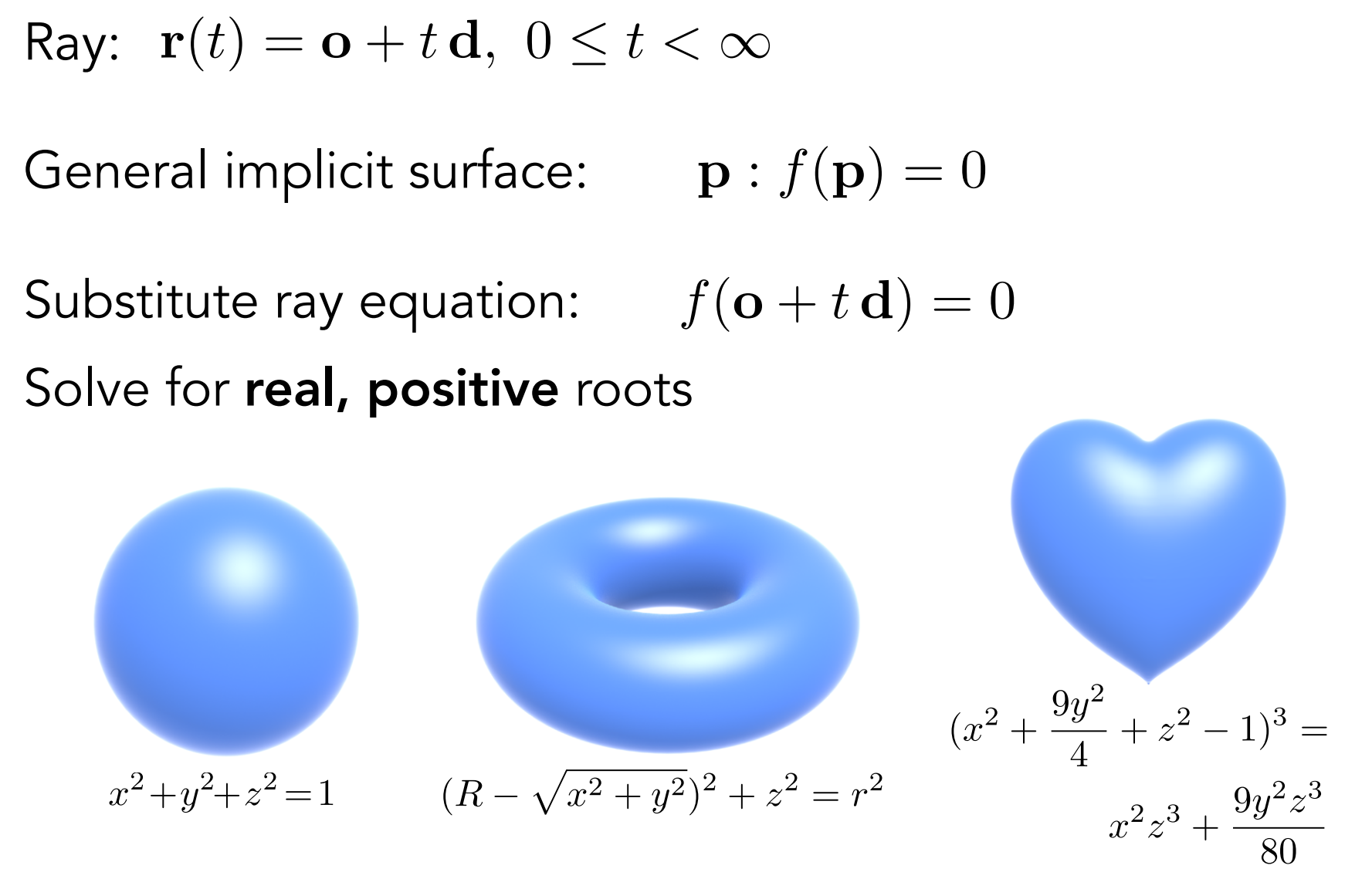
c.1.2). 与三角形求交：

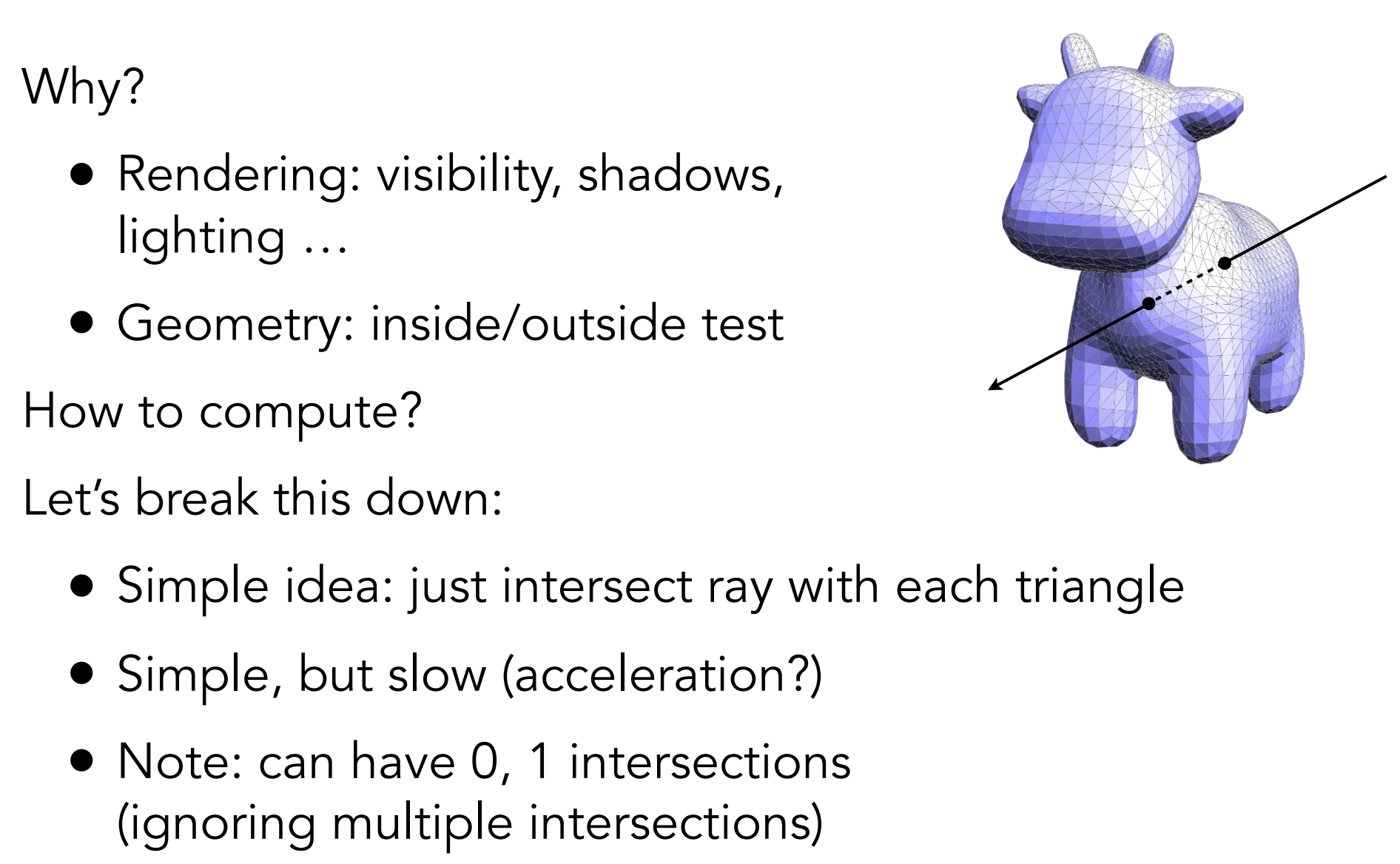
• 几何上：判断内外；

  • 空间内任意一点为起点做一光线，若该光线与object（封闭）交点数为奇数，则该点在object内；若交点数为奇数，则该点在object外；（缠绕数的奇-偶原则）

• 计算过程：

  • 

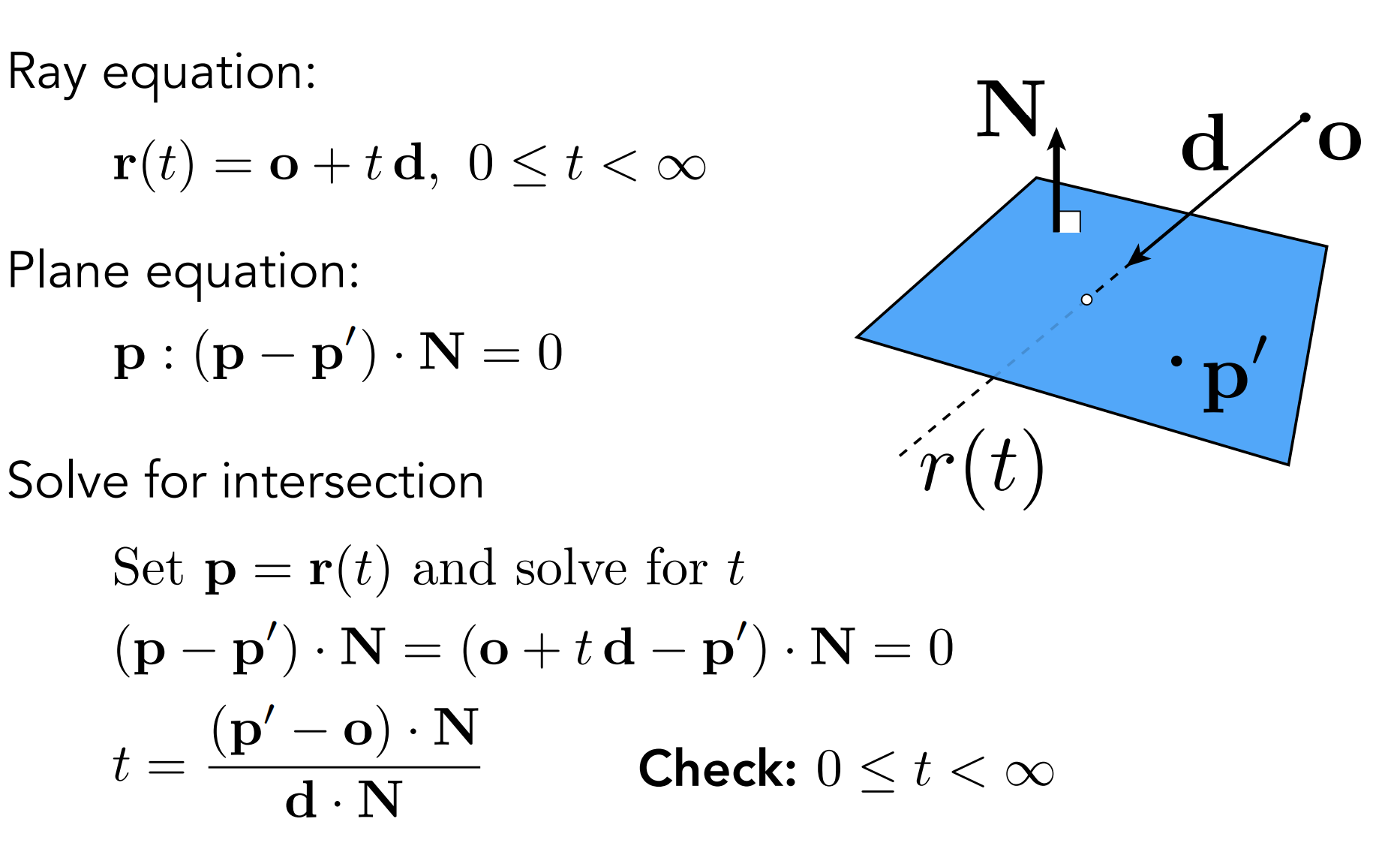
  • 即 $r(t)=o+td,0\leq t < \infty$ 和 $(p-p’)·N=0$ 联立求 $t$；

  • 之后求得点P是否在三角形内；

• Möller Trumbore Algorithm

  • 按传统求解，求出 $t$ 后，还需要判断 P 点是否在三角形内，较为繁琐，因此提出Möller Trumbore Algorithm
  • 
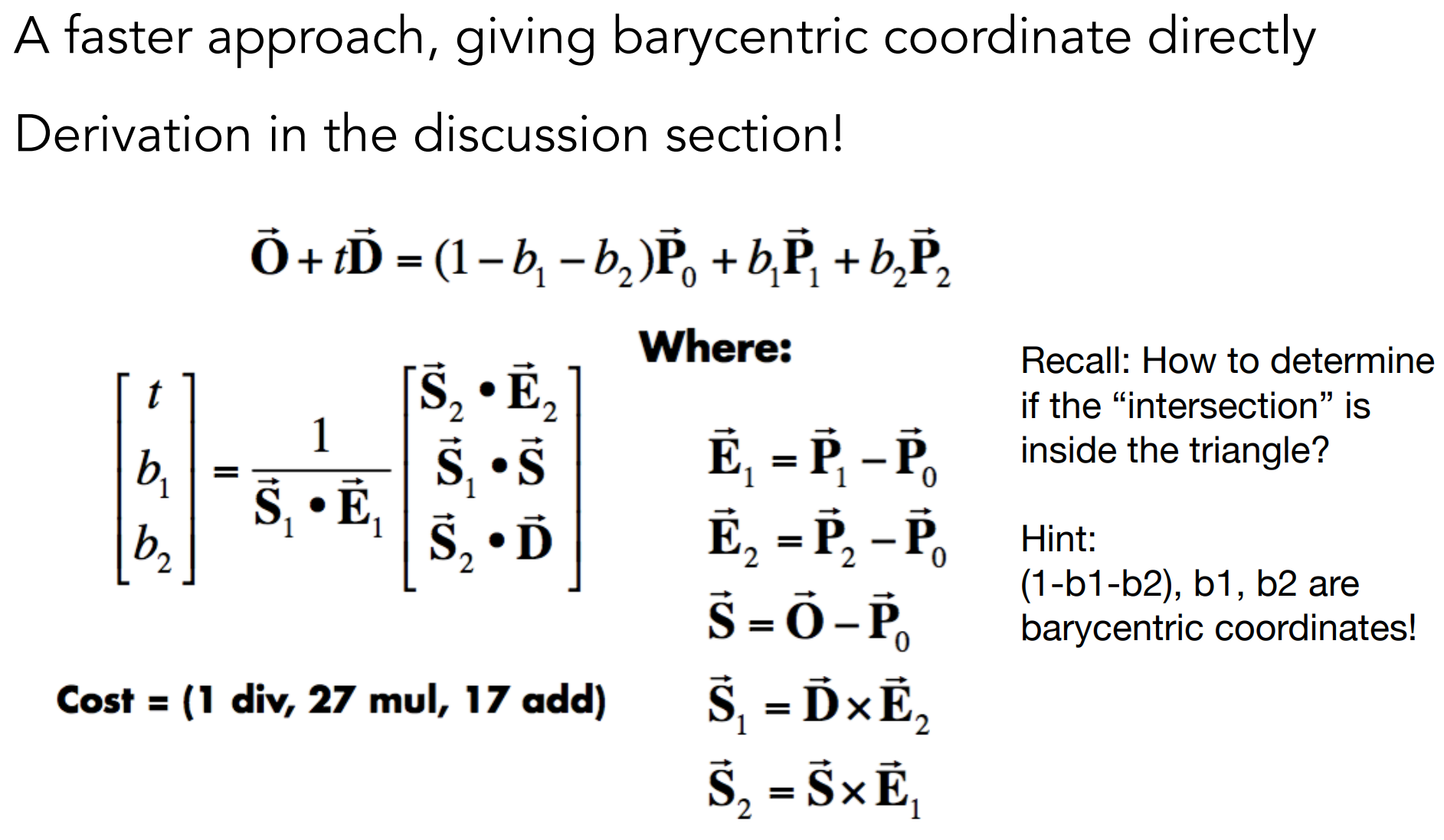
    • 射线$r(t)=O+tD$ ，与由重心坐标表示的三角形上的点 $P$ 求解（三个式子，三个未知量，根据克拉默必定有解）；
    • 求得交点后，可通过重心坐标得知该点是否在三角形外；

c.2). Acclerating Ray-Surface Intersection

• 原因：当需要求得光线最近的交点时，需要遍历场景所有三角面，速度慢，需要加速；

c.2.1). Axis-Aligned Bounding Box(AABB，轴对齐包围盒)

• Bounding Volumes

  • 思想：当物体不与包围体积相交时，更不可能和物体相交；

  

• Bounding Box（AABB for example）：

  • 理解：盒子是3对对立的面的交集；
  • Axis-Aligned Bounding Box(AABB)
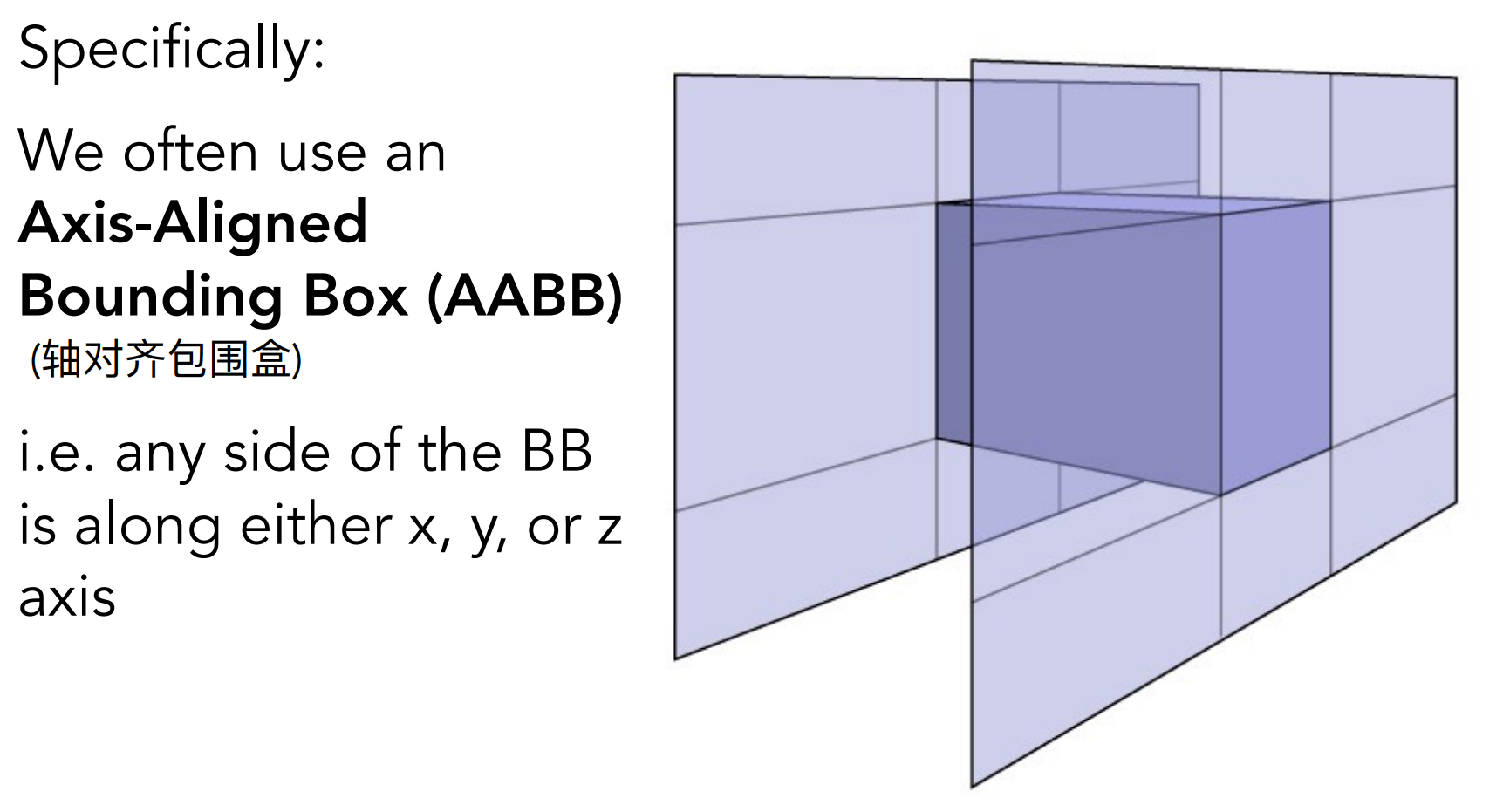
    • AABB包围盒的面总在xy/xz/yz平面；

• 光线与AABB求交：

  • 2D情况下（3D同理）
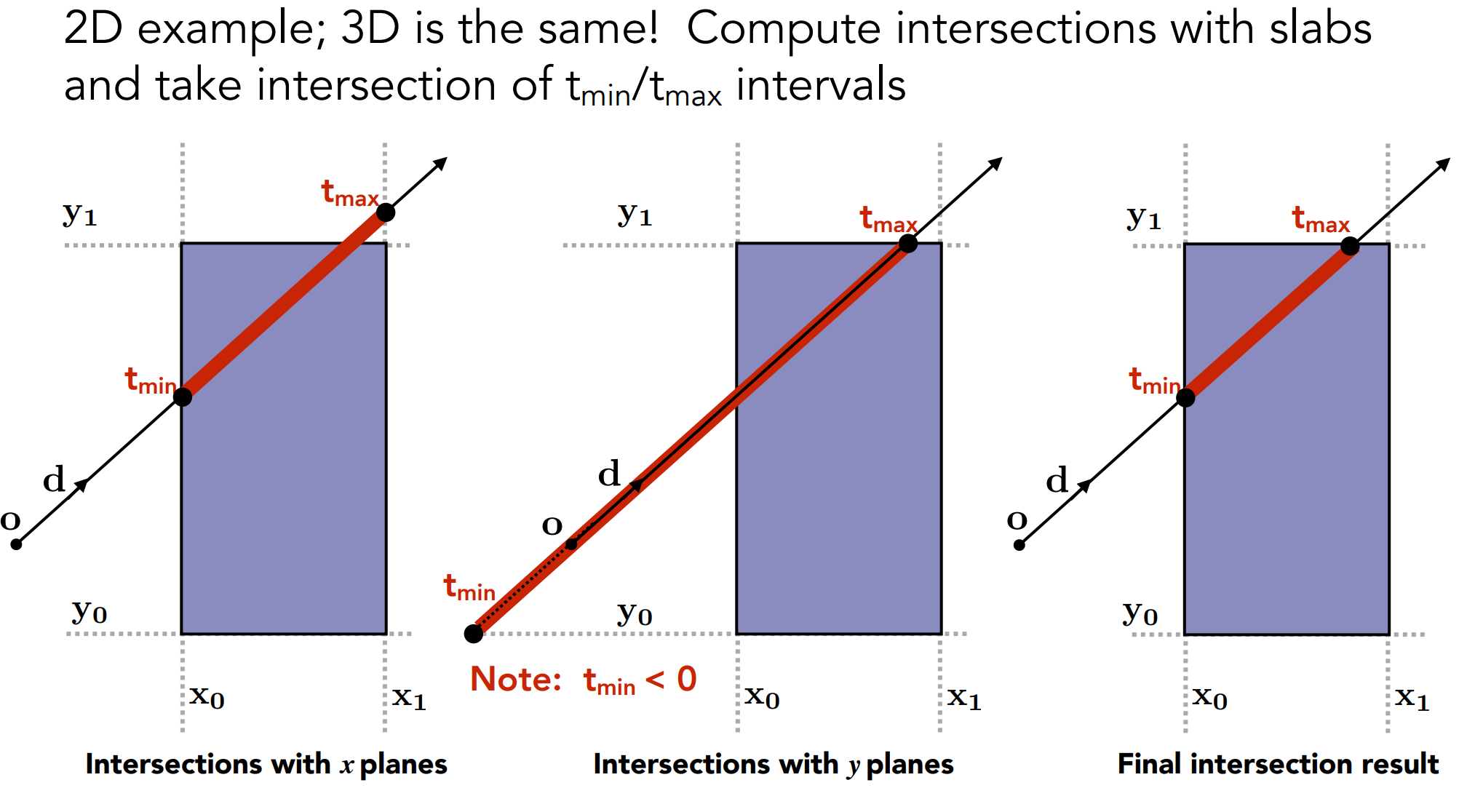
  • 思想：
    • 光线进入Box：只有当光线进入所有的对立面；
    • 光线出Box：只要光线出射一个对立面；
    • 对于3D的Box，$t_{enter}=max\{t_{min}\},t_{exit}=min\{t_{max}\}$；
    • 如果 $t_{enter}<t_{exit}$，则光线经过Box；
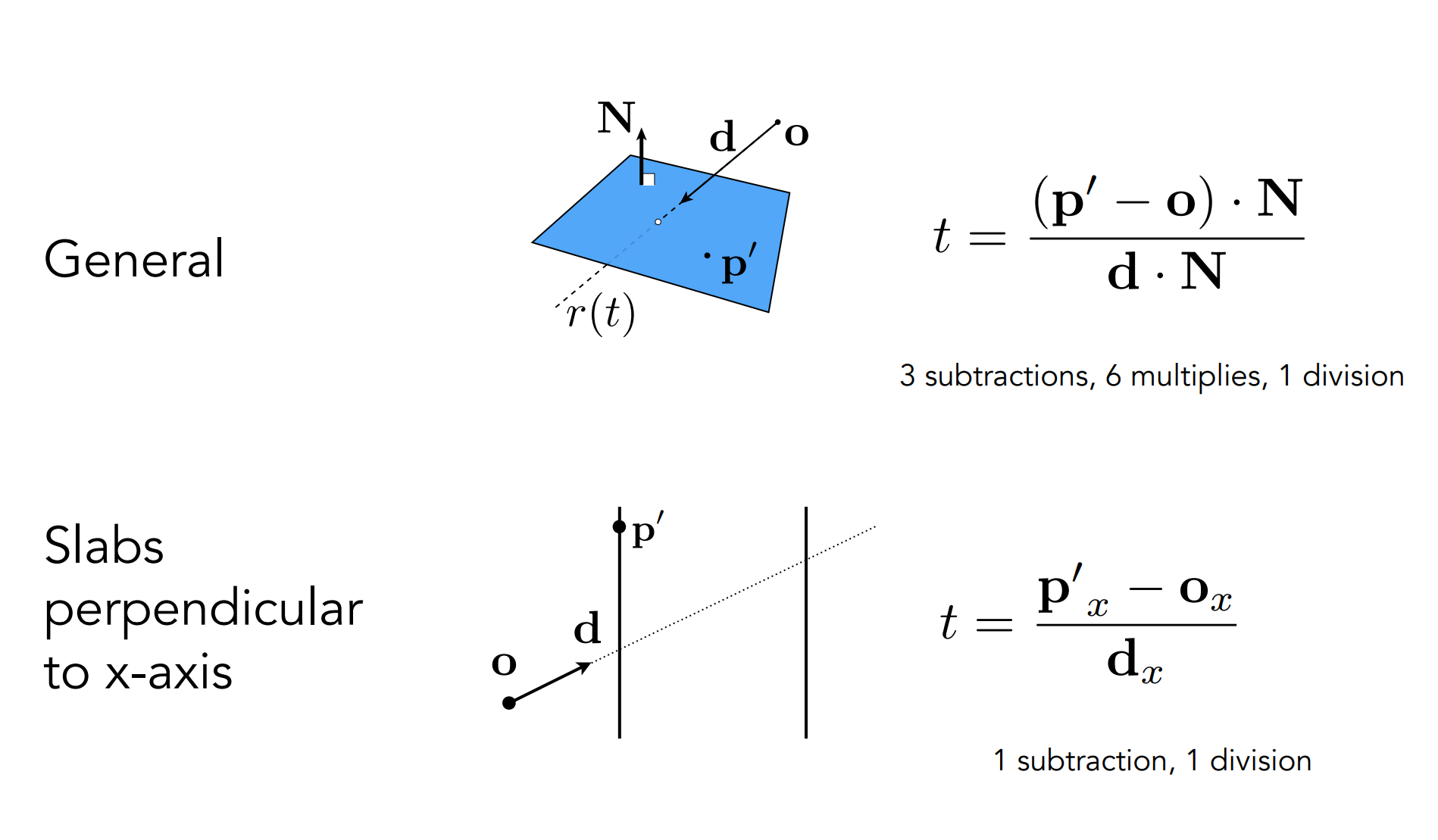
  • 对于 $t_{enter}$ 和 $t_{exit}$ 正负情况的考虑：
    • $t_{exit}<0$：不相交（Box在光线后边）
    • $t_{exit}<0$ and $t_{enter}<0$：光线起点在盒子里，一定相交
    • 当且仅当 $t_{enter}<t_{exit}\quad\&\&\quad t_{exit}\geq0$，光线与AABB相交；
• 为什么使用AABB：求交方便；

Lecture 14&15 Ray Tracing(Acceleration & Radiometry; Light Transport & Global Illumination)

a). Uniform Spatial Partitions（统一空间分区）

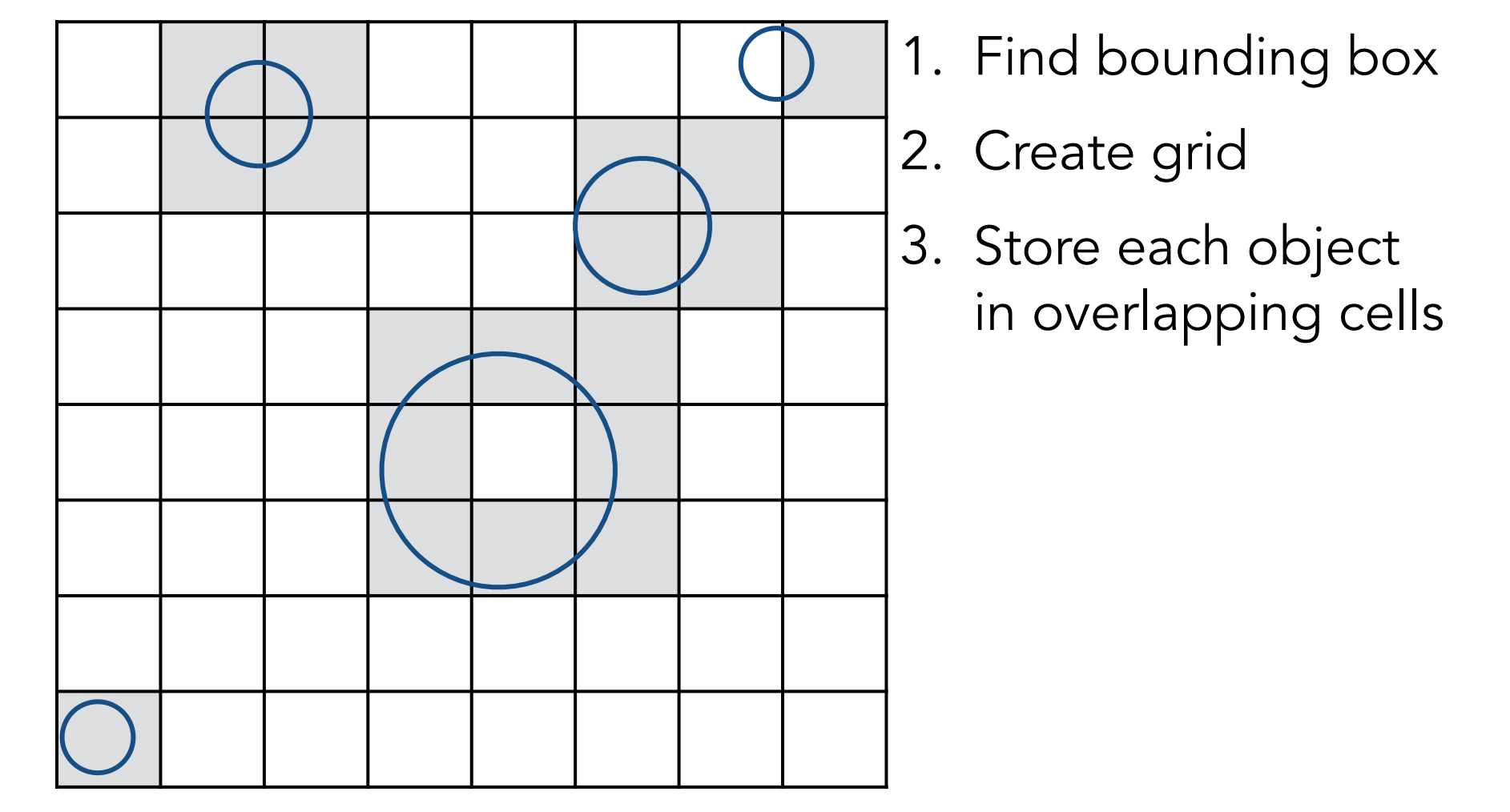
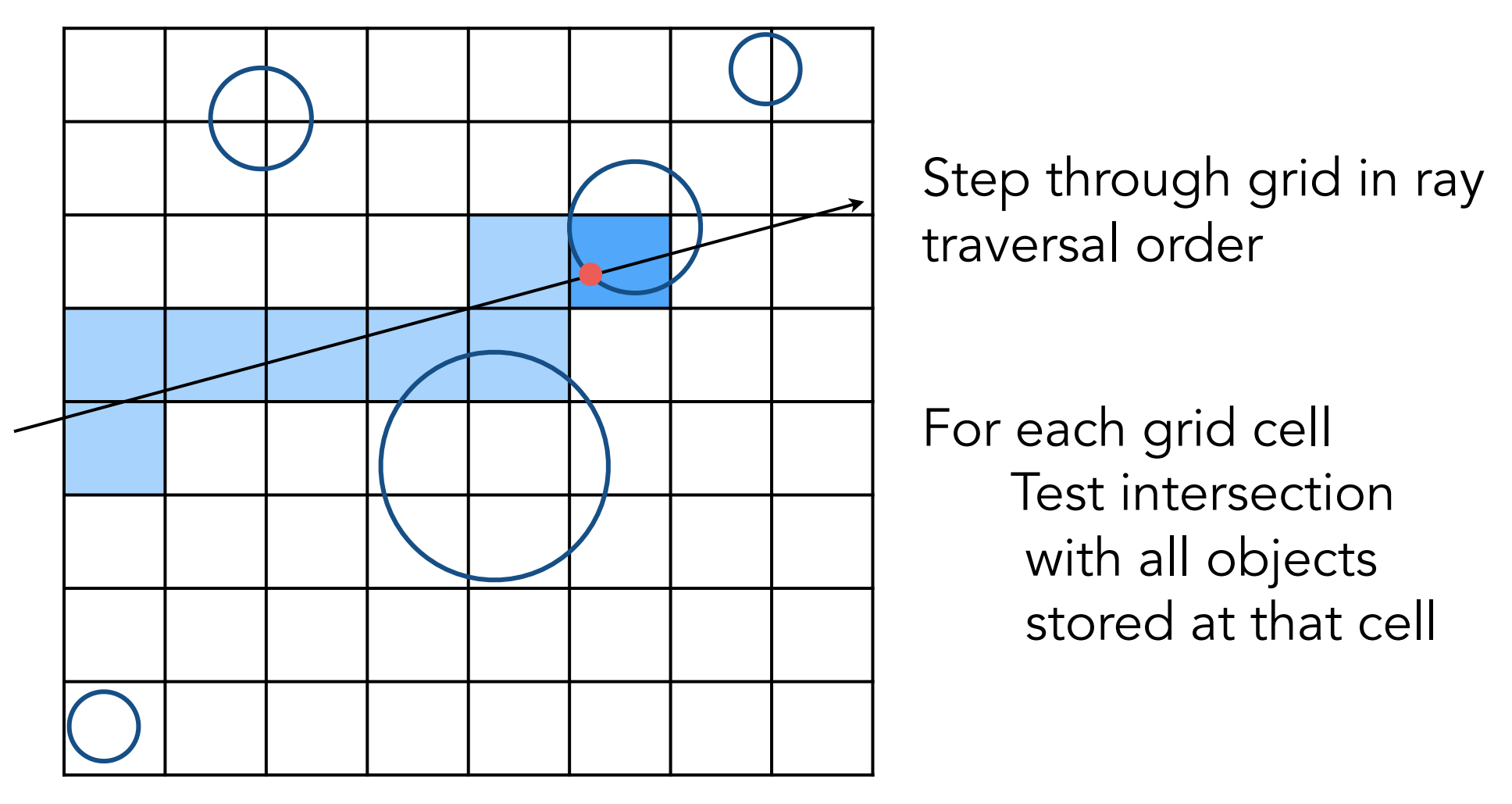
• Heuristic:

  • #cells = C * #objs
  • C ≈ 27 in 3D

• 缺陷：

  • 格子大小相同，浪费空间；
  • 对于空间分布不均匀的场景容易造成“Teapot in a stadium” problem，浪费性能；

b). Spatial Partition

• 常见的空间划分的类型：
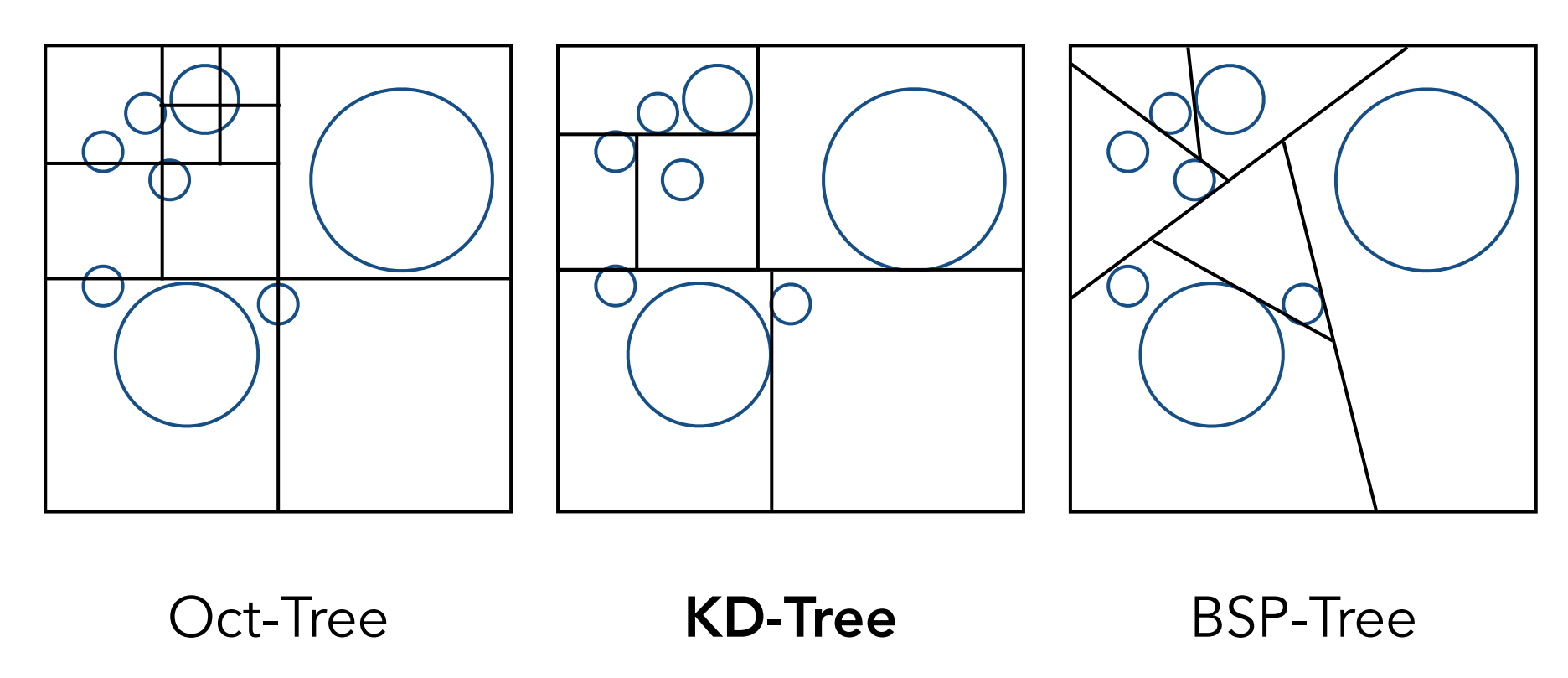
  • Oct-Tree（3维中是八叉树，2维中是四叉树；$2^n$叉树，n=维度）
    • 受维度影响；
  • KD-Tree；
    • 每次只划分一次，如果是三维则按x，y，z方向循环划分；
  • BSP-Tree

b.1). KD-Tree

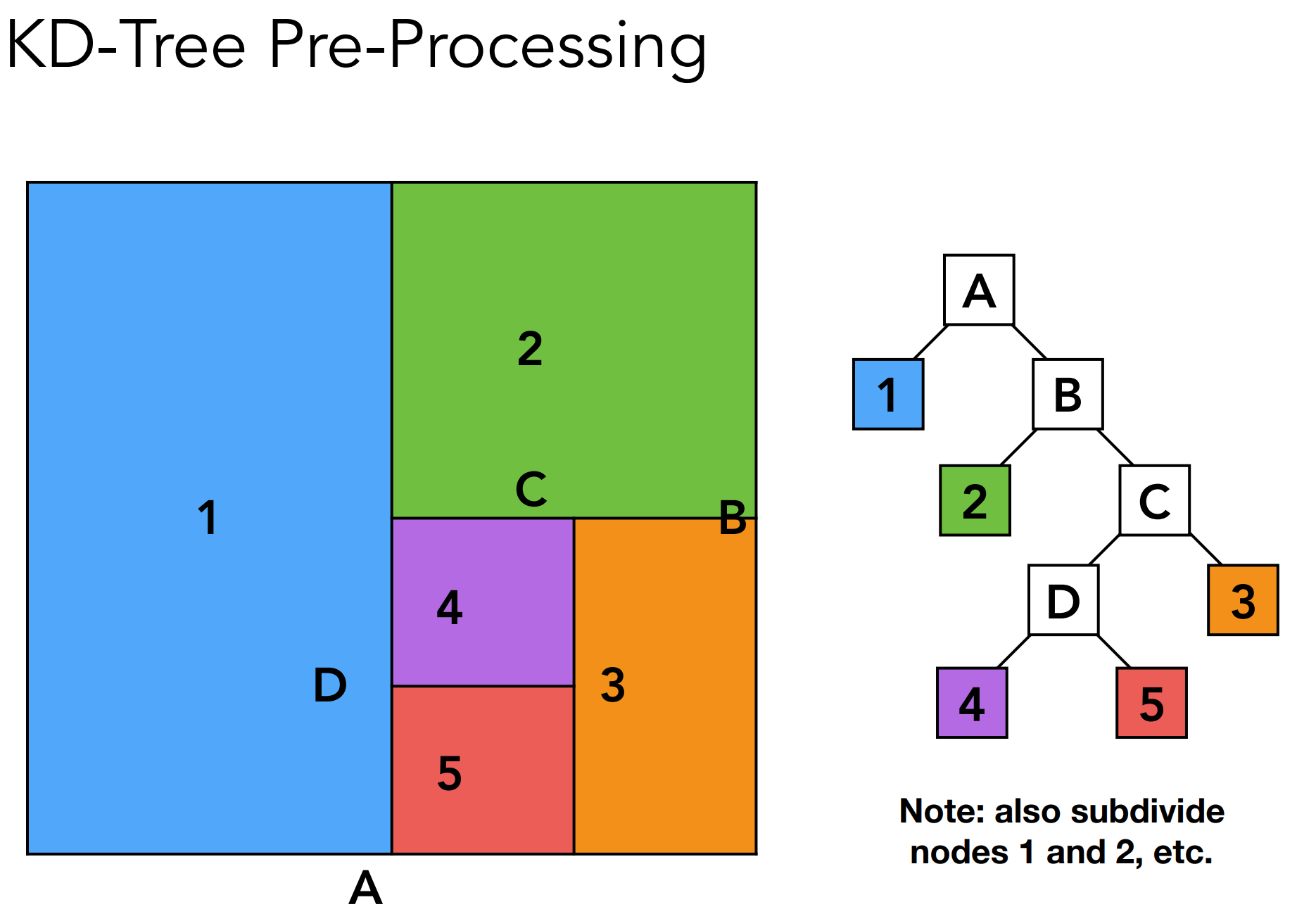
• 预处理：对空间进行划分，对于子空间每次只划分一次（1、2、3划分省略）；
  • 树节点（Internal node）的数据结构：
    • 划分轴：x-, y- , or z-axis;
    • 划分位置：分割平面沿轴的坐标；（？）
    • 子节点；
    • 不存储object；
  • 叶子节点数据结构：
    • object的列表

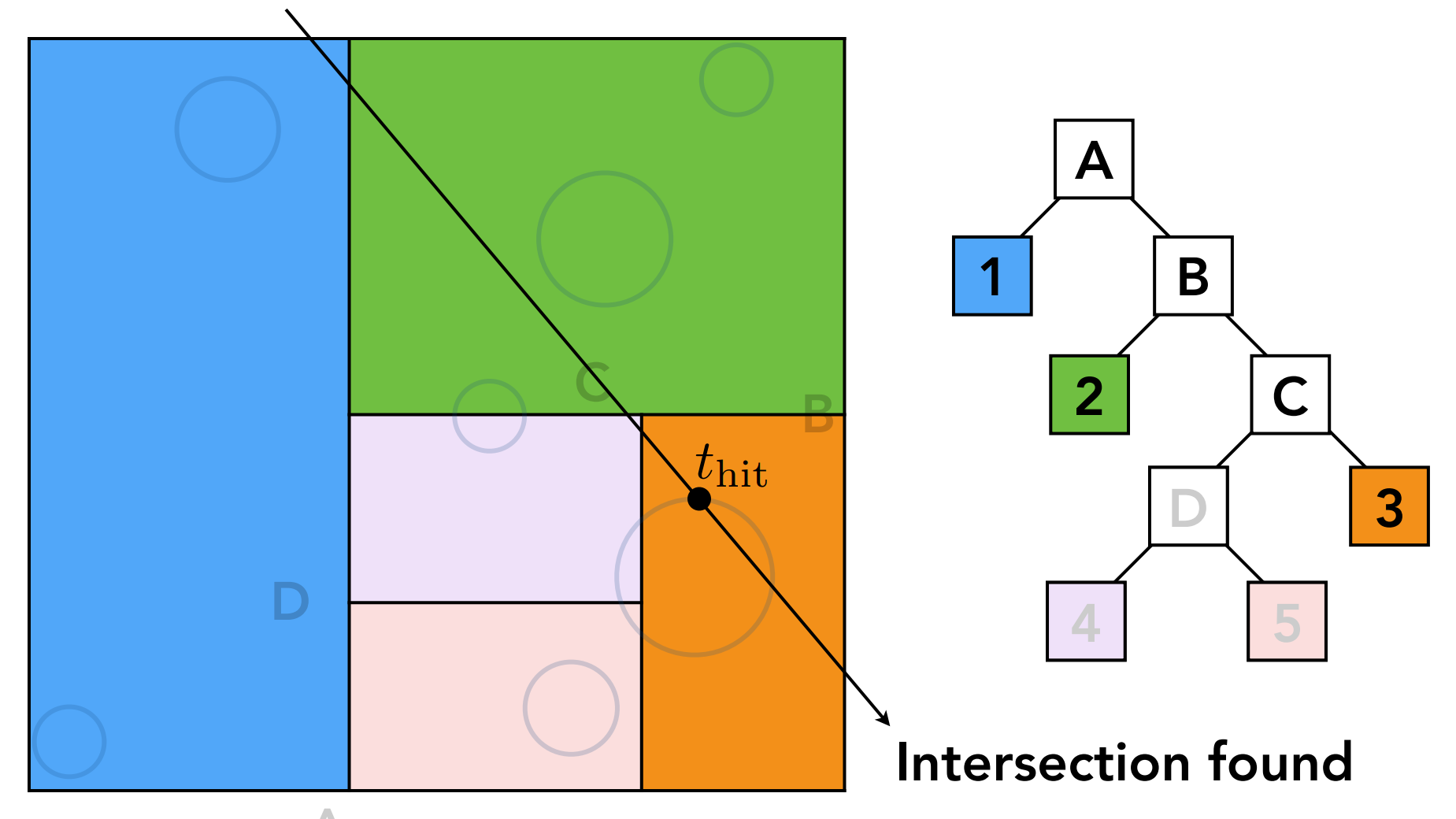
• 过程：
  • 光线和叶子节点1（为方便把$1$暂看作叶子节点，尽管个节点应该继续划分，$2,3$同理）相交，判断光线和$1$中储存的object是否相交（无相加，继续）；
  • ……
  • 光线和叶子节点3相交，判断光线和$1$中储存的object是否相交，相交，记录$t_{hit}$；
• 缺点：
  1. 预处理的过程中，物体（三角形）和网格求交难；
     • 如三角形和Box求交，有可能是一个小Box穿过三角形（被三角形“包裹”）
  2. 同一个Object可能储存在多个叶子节点中；

c). Bounding Volume Hierarchy (BVH)

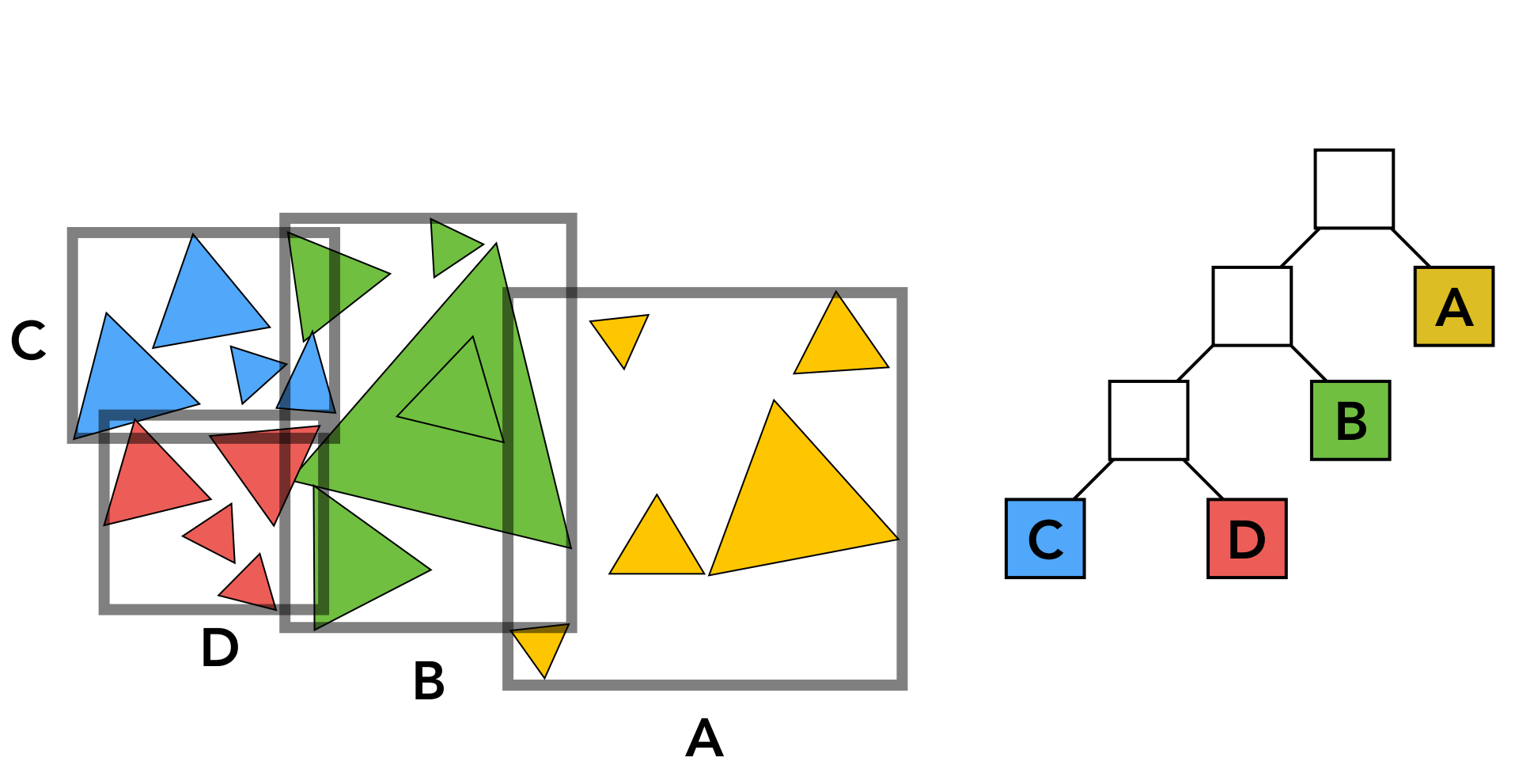
• 特征：先将object分为两组，再重新计算包围盒，使得同一个obejct只会在一个叶子节点中出现；（但会造成Bounding Box空间的冗余）
• 过程：
  • 找到包围盒；
  • 递归地将物体的集分为两个子集；
  • 重新计算子集的包围盒；
  • 满足条件时停止；
  • 储存objects到对应的叶子节点；
• 划分子节点：
  • 选择一个维度去划分；
  • Heuristic #1: 选择最长的轴去划分；
  • Heuristic #2: 选择中间的object的位置去划分；（快速选择算法）
• BVHs的数据结构：
  • 非叶子节点：
    • Bounding box
    • Children: pointer to child nodes
  • 叶子节点：
    • Bounding box
    • List of objects
  • Nodes represent subset of primitives in scene

• BVH Traversal:

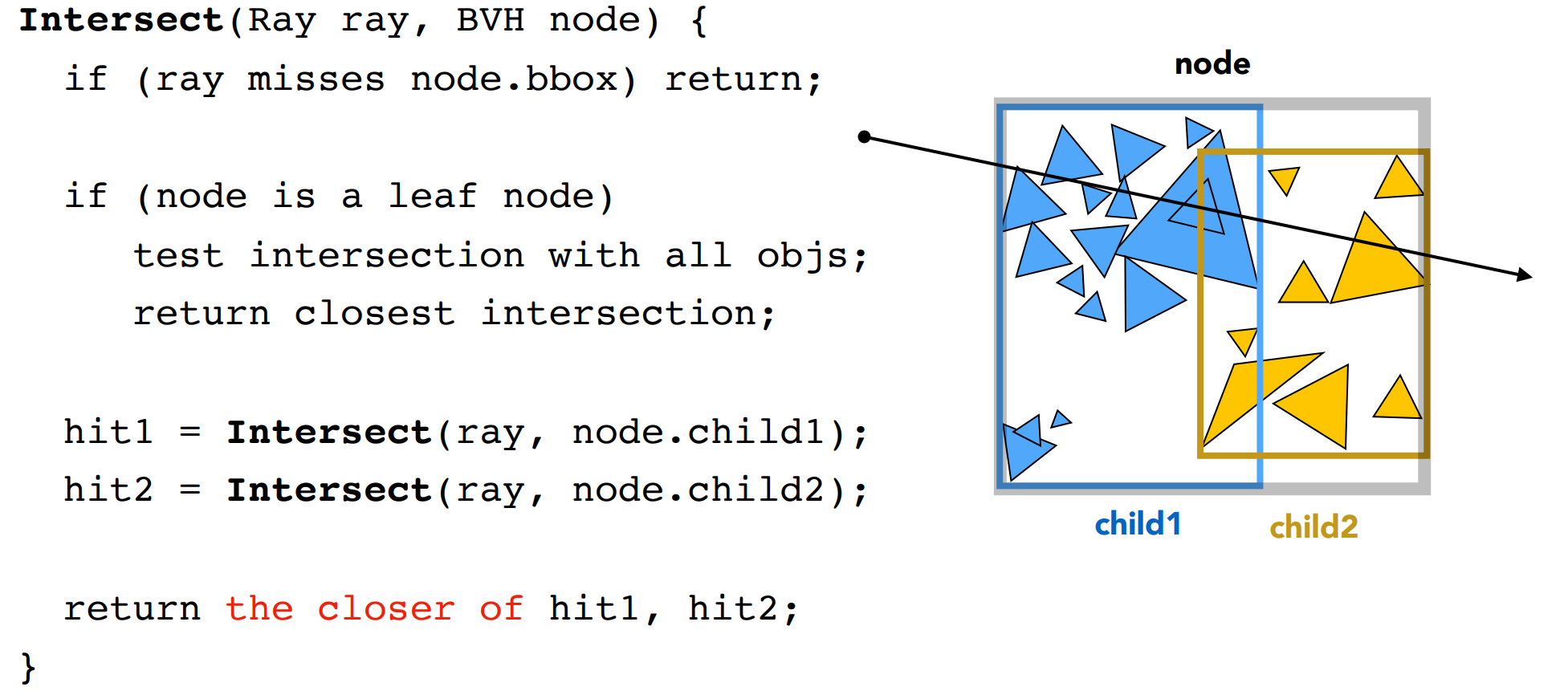
• 空间划分和物体划分:

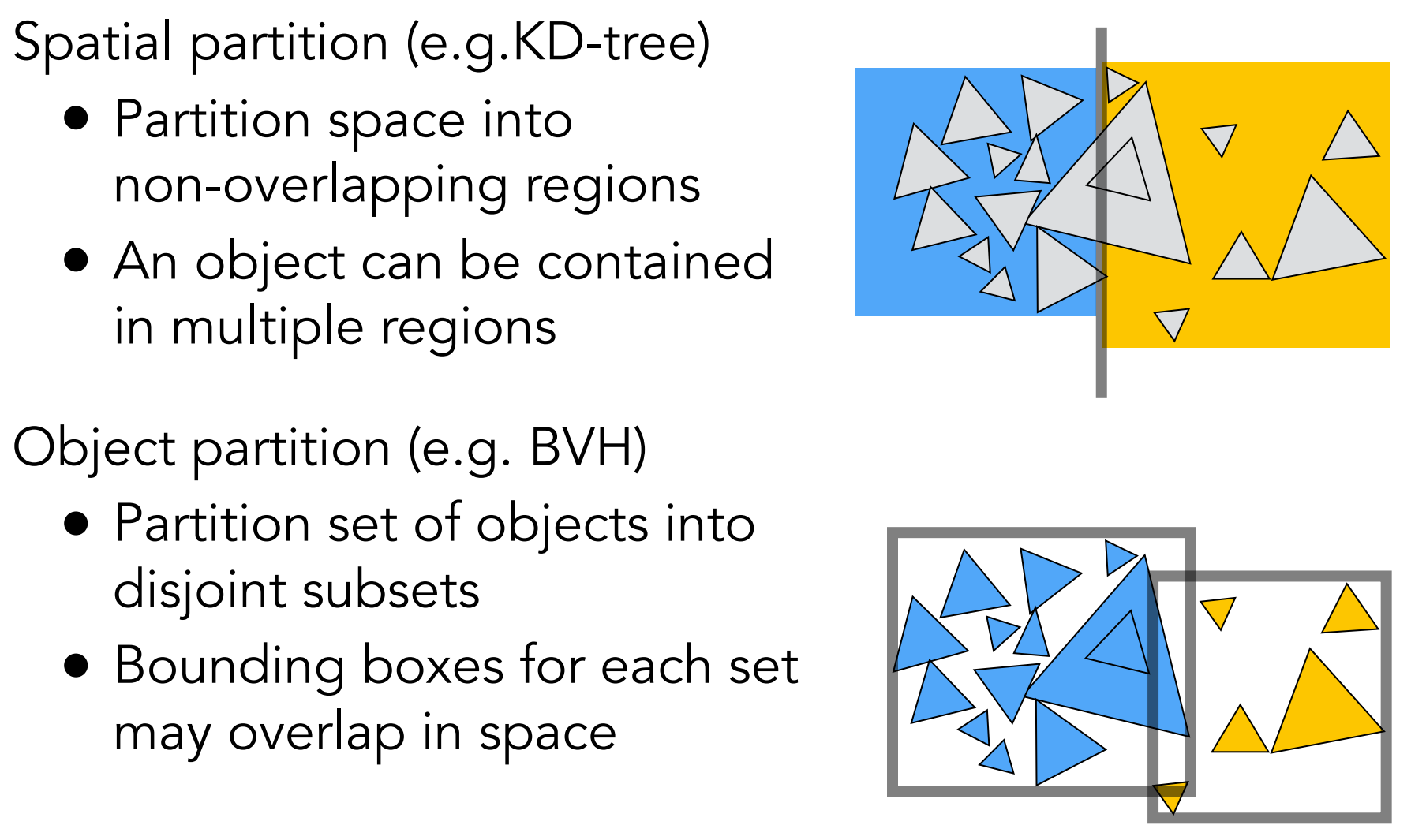
d). Radiometry

d.1). Radiant Energy and Flux(Power)

• Radiant Energy(辐射能量):
  • Definition: Radiant energy is the energy of electromagnetic radiation. It is measured in units of joules, and denoted by the symbol:

$$Q[J=Joule]$$

• Flux(辐射通量):

  • Definition: Radiant flux (power) is the energy emitted, reflected, transmitted or received, per unit time.
  $$\Phi \equiv \frac{\mathrm{d} Q}{\mathrm{~d} t}[\mathrm{~W}=\mathrm{Watt}][\operatorname{lm}=\text {lumen}]$$

• Important Light Measurements of Interest

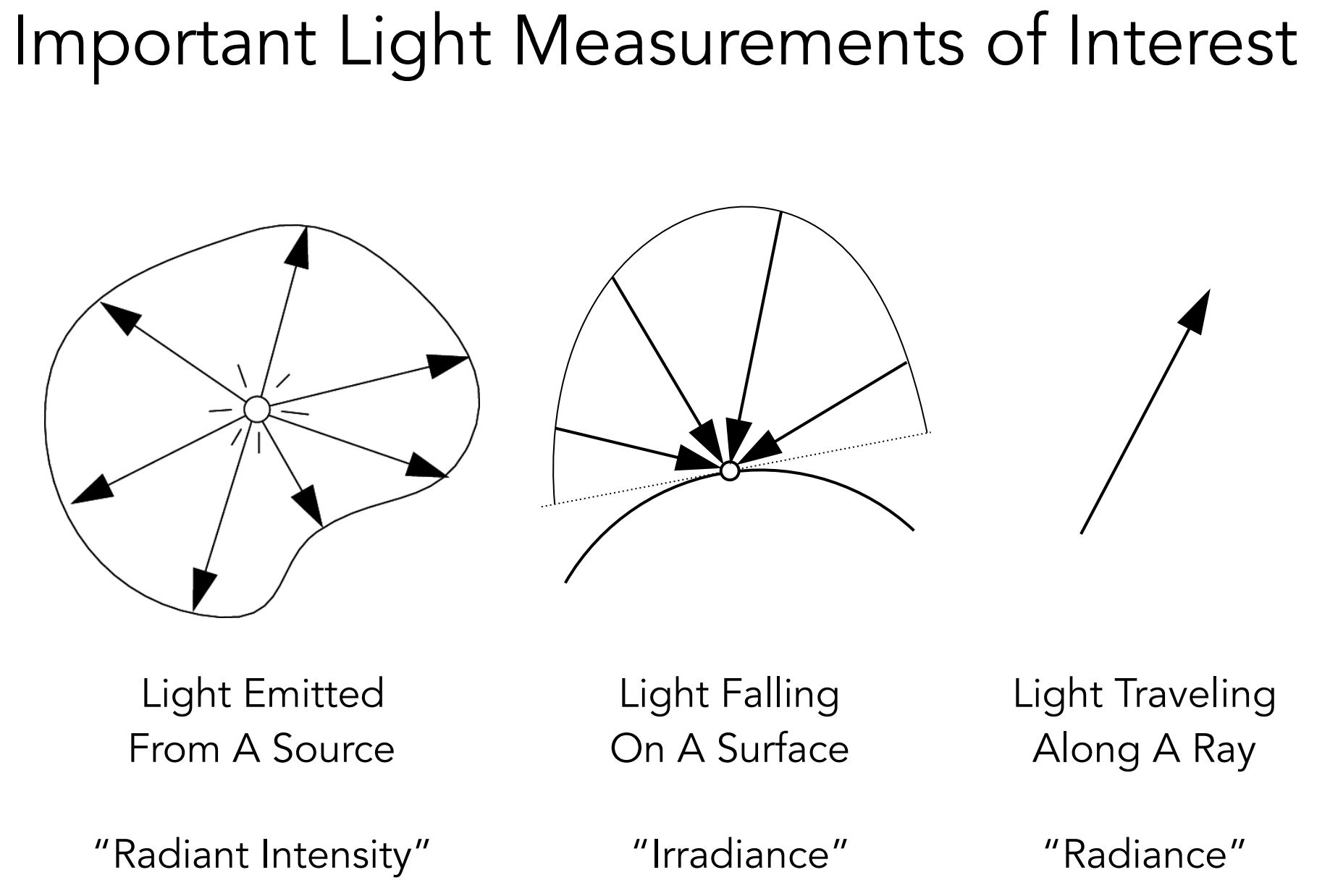
d.2). Radiant Intensity(辐射强度)

• 定义：单位立体角上，产生的、反射的、接收的辐射通量。符号：I；单位：瓦特/sr、lm/sr、candela、cd。 立体角(solid angle)是有方向的，所以辐射强度是一个方向有关的属性

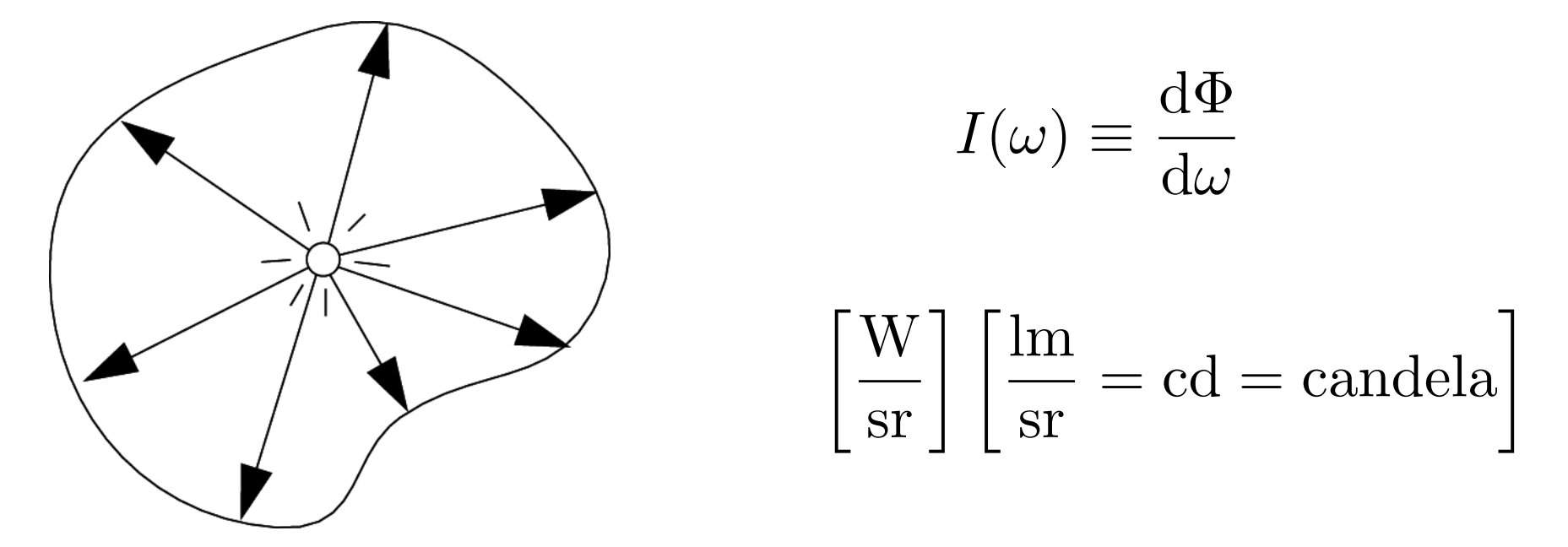
d.2.1). Solid angle

• 角度（2D）： 弧长除以半径；
  • $\theta={l\over r}$
• 立体角：立体角面积除以半径的平方
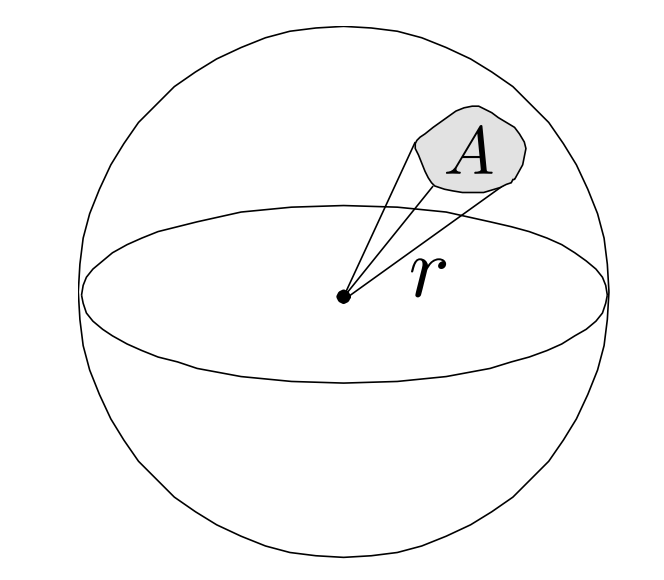
  • $\Omega=\frac{A}{r^{2}}$
  • 球体的立体角为$4\pi$

d.2.2). 计算过程

• 立体角微分：

  • 

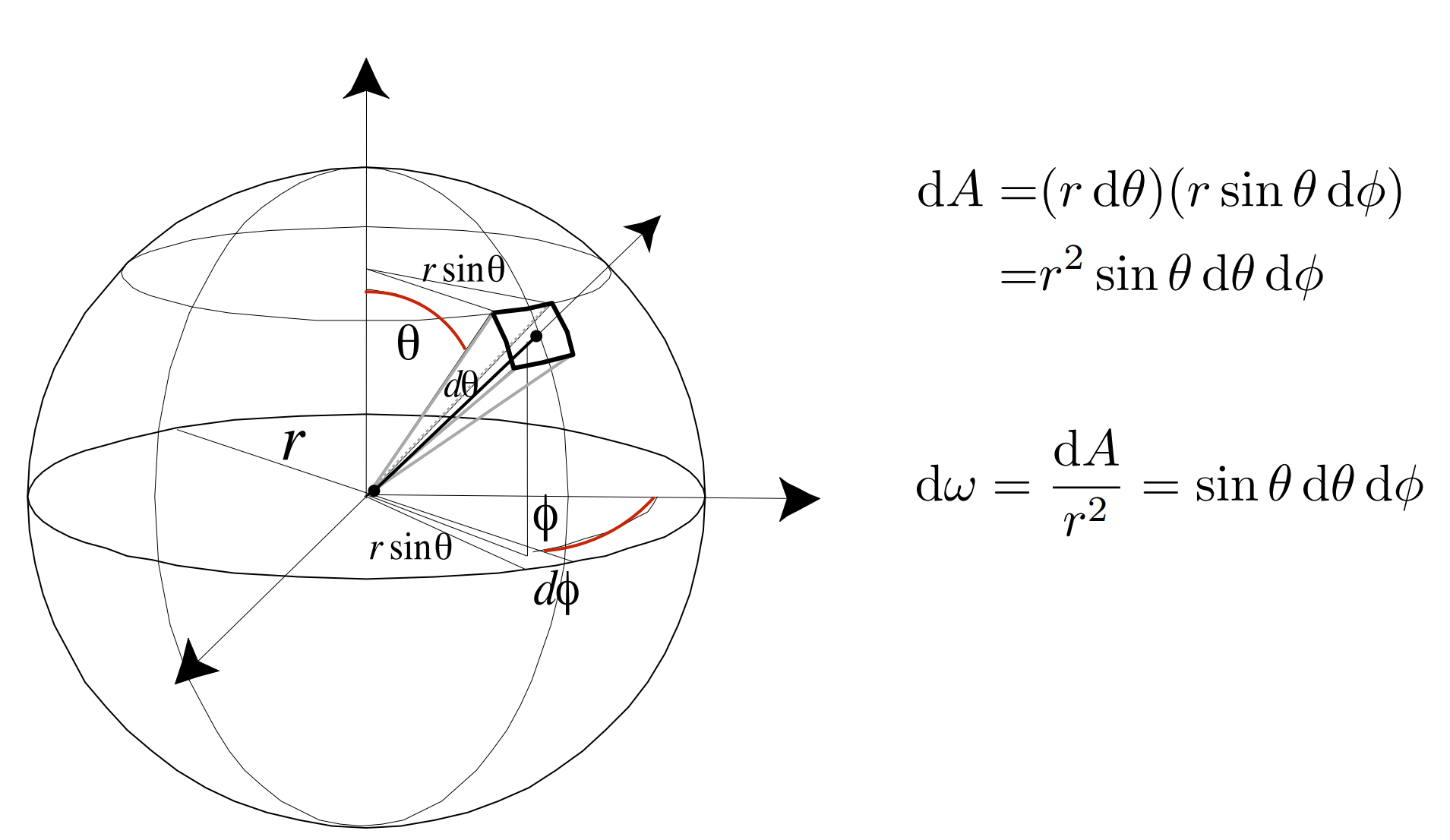
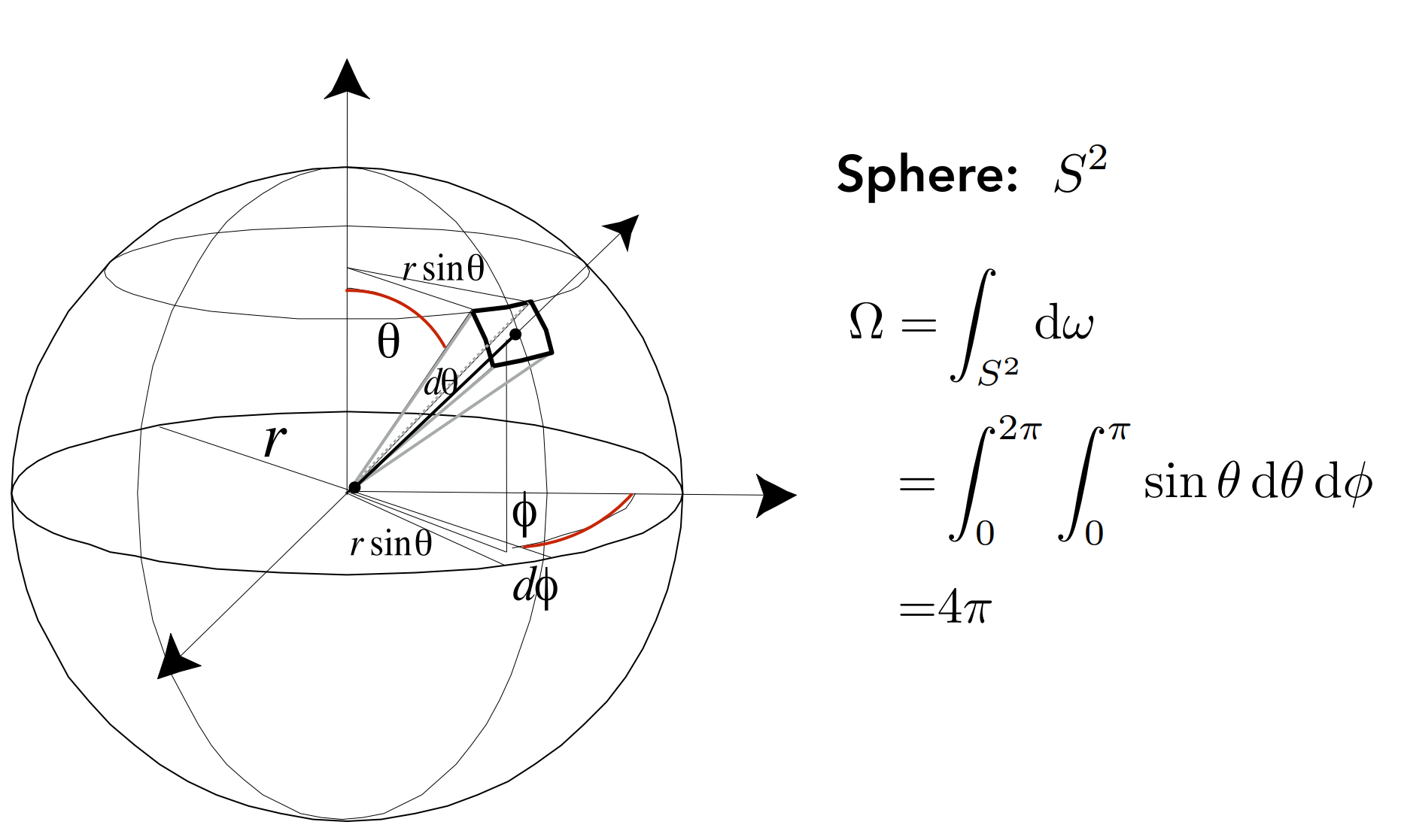
  • 二重积分计算，总的立体角 = 球面上无数个单位立体角的加和，即∫∫sinθdθdφ
    积分限也比较好理解：θ：0 → π，一个半圆弧， φ：0 → 2π，用半圆转一整圈得到球面

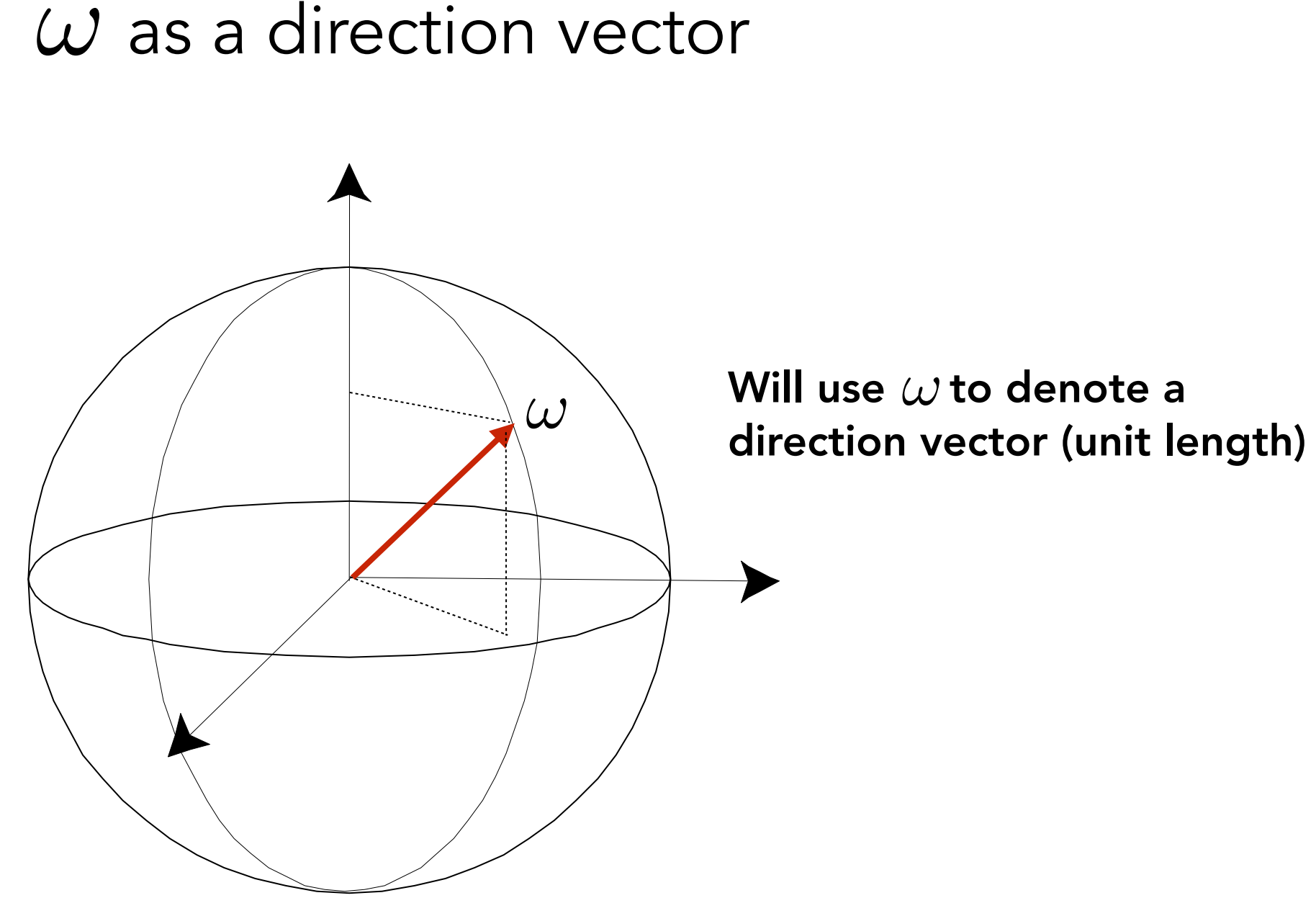
• 通常把ω当做方向向量来理解，这样比较好描述intensity

• 如果点光源向三维空间中均匀的辐射出能量，怎么描述强度？

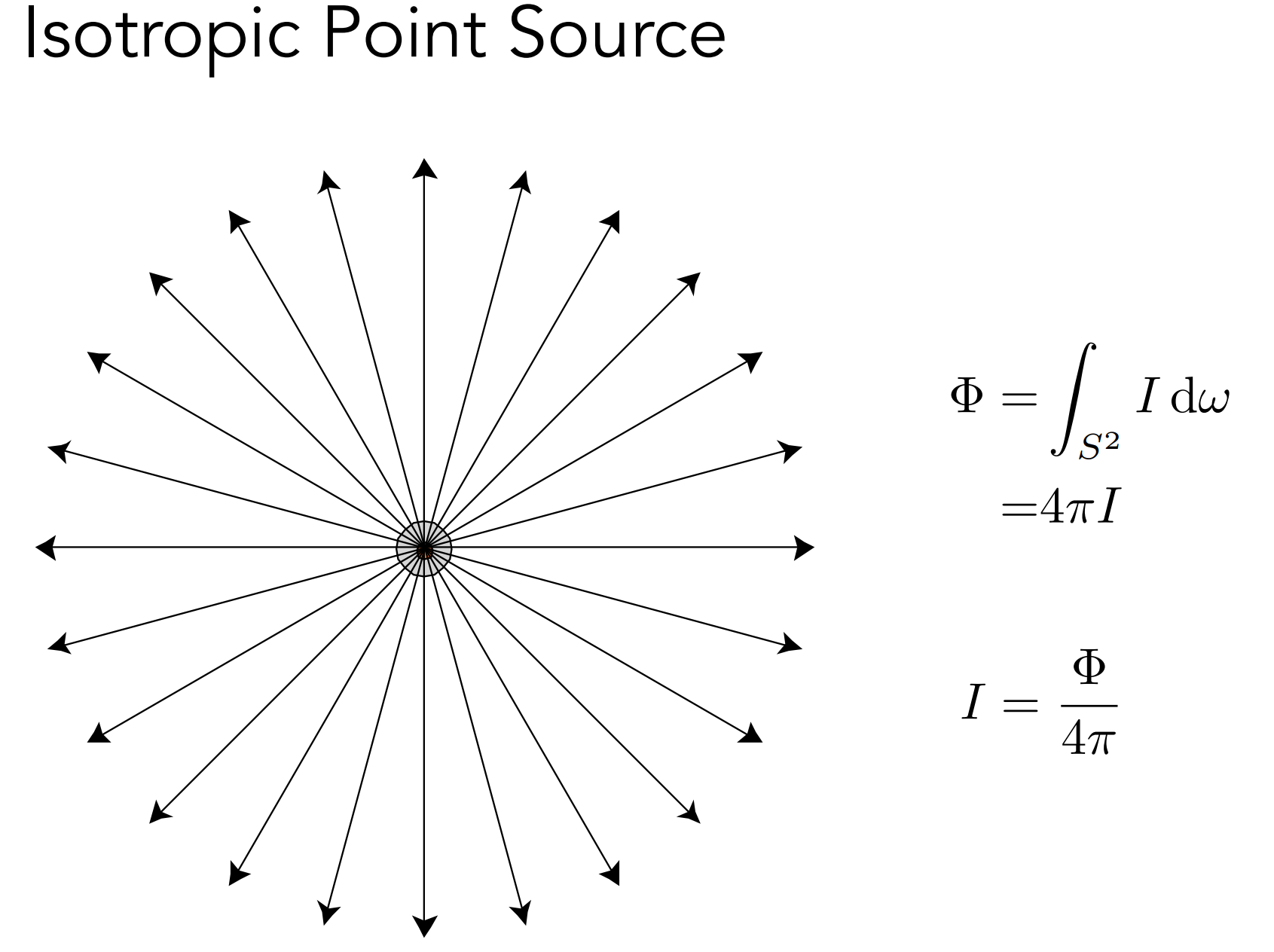
  I = Φ / 4π
  Φ：点光源单位时间内，向三维空间中辐射出的能量
  4π：整个三维空间的总立体角
  其比值就是单位立体角上的辐射通量

d.2.3). Irradiance(辐照度)

• 定义：每单位面积（与光线垂直，Lambert’s Cosine Law）的能量

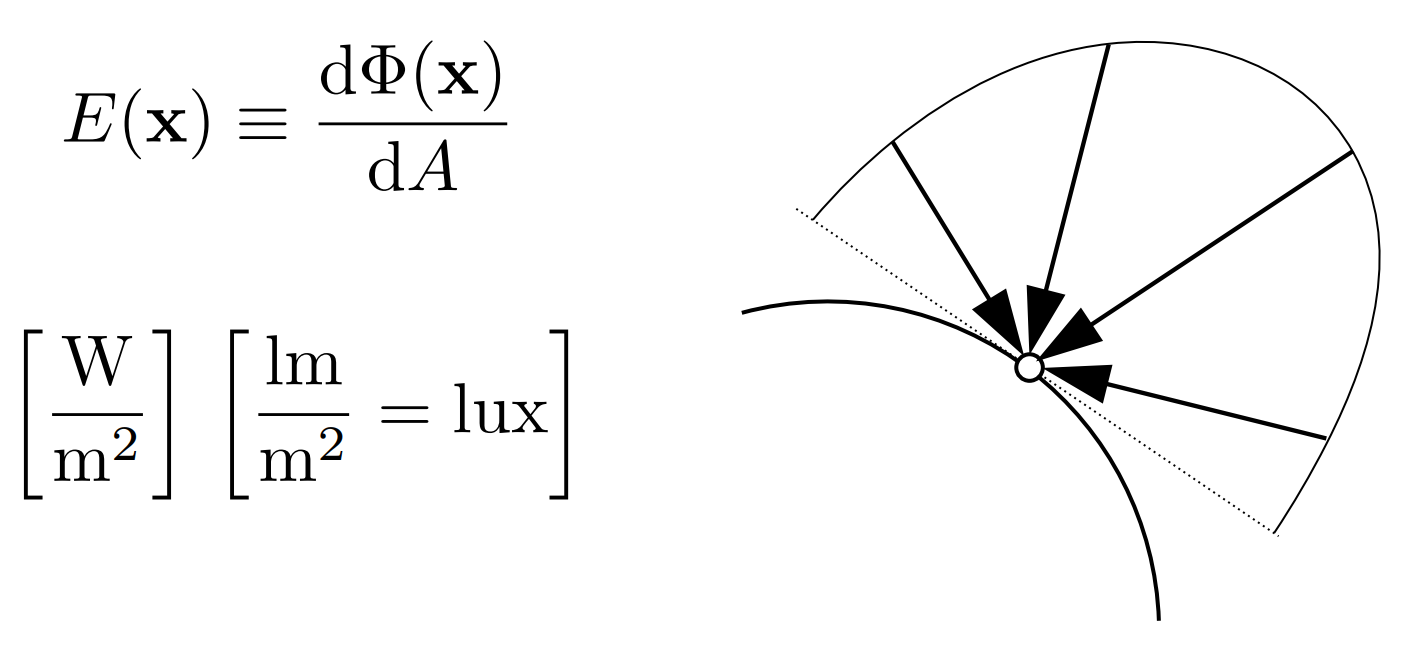
• Lambert’s Cosine Law

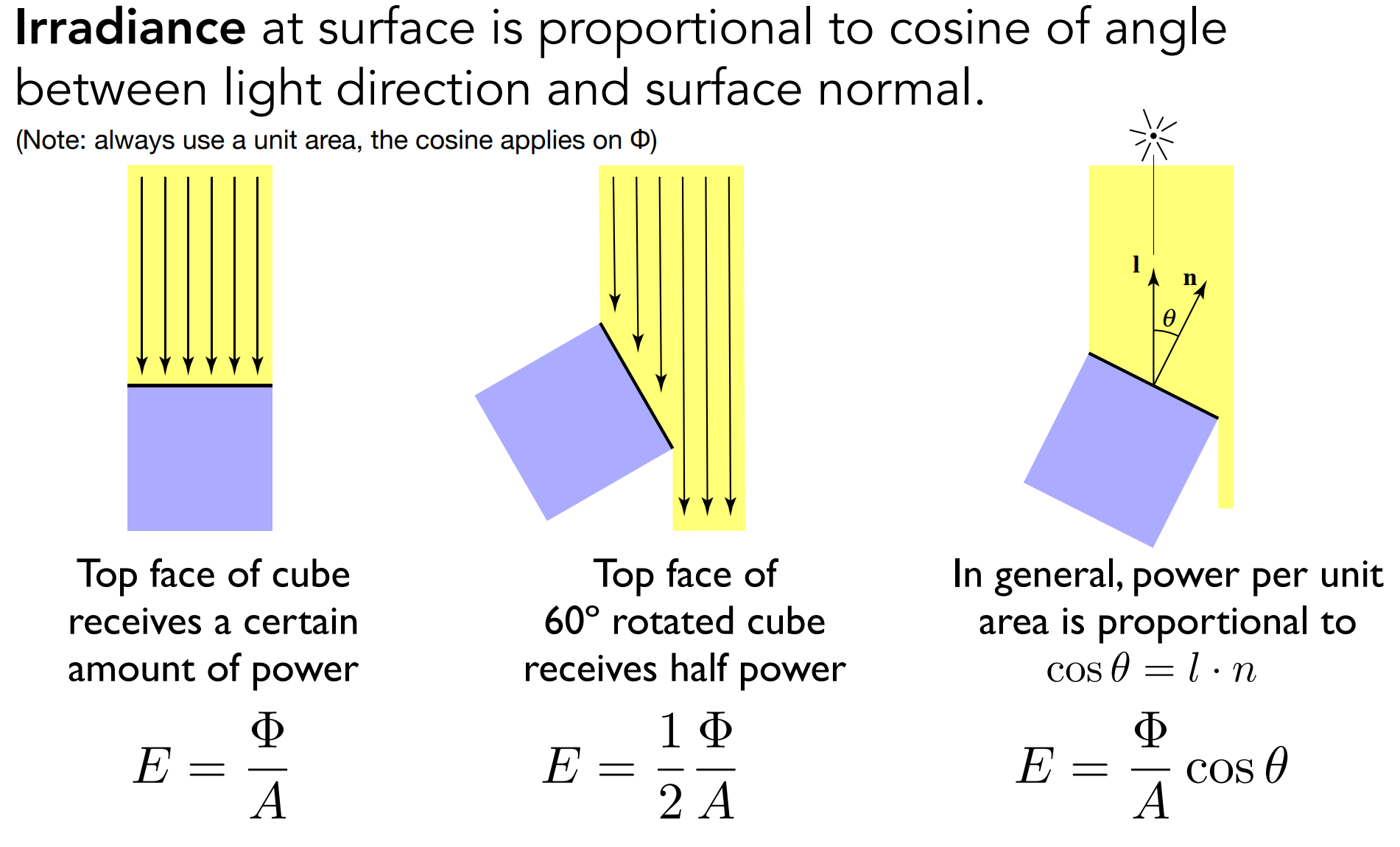
  • e.g. 太阳高度角造成四季变化
• 
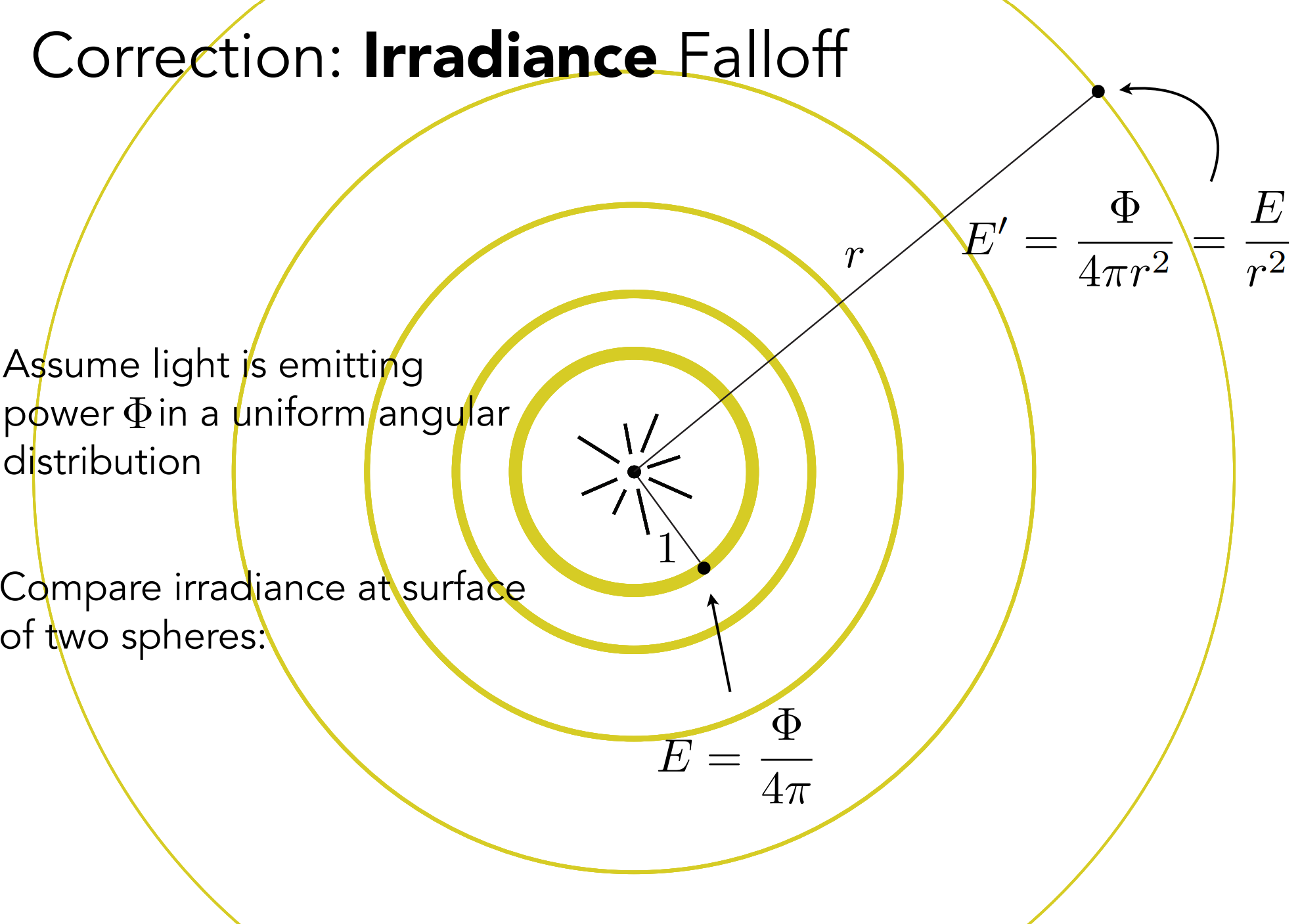
  • 随半径变大，Irradiacne变小，而radiant intensity不变；

d.2.4). Radiance(辐亮度)

• 介绍：

  • Radiance是和光线有关的量；
  • 渲染就是在计算radiance；

• 单位：The radiance(luminance) is the power emitted. reflected, transmitted or receivedd by a surface, per unit solid angle, per projected unit area.

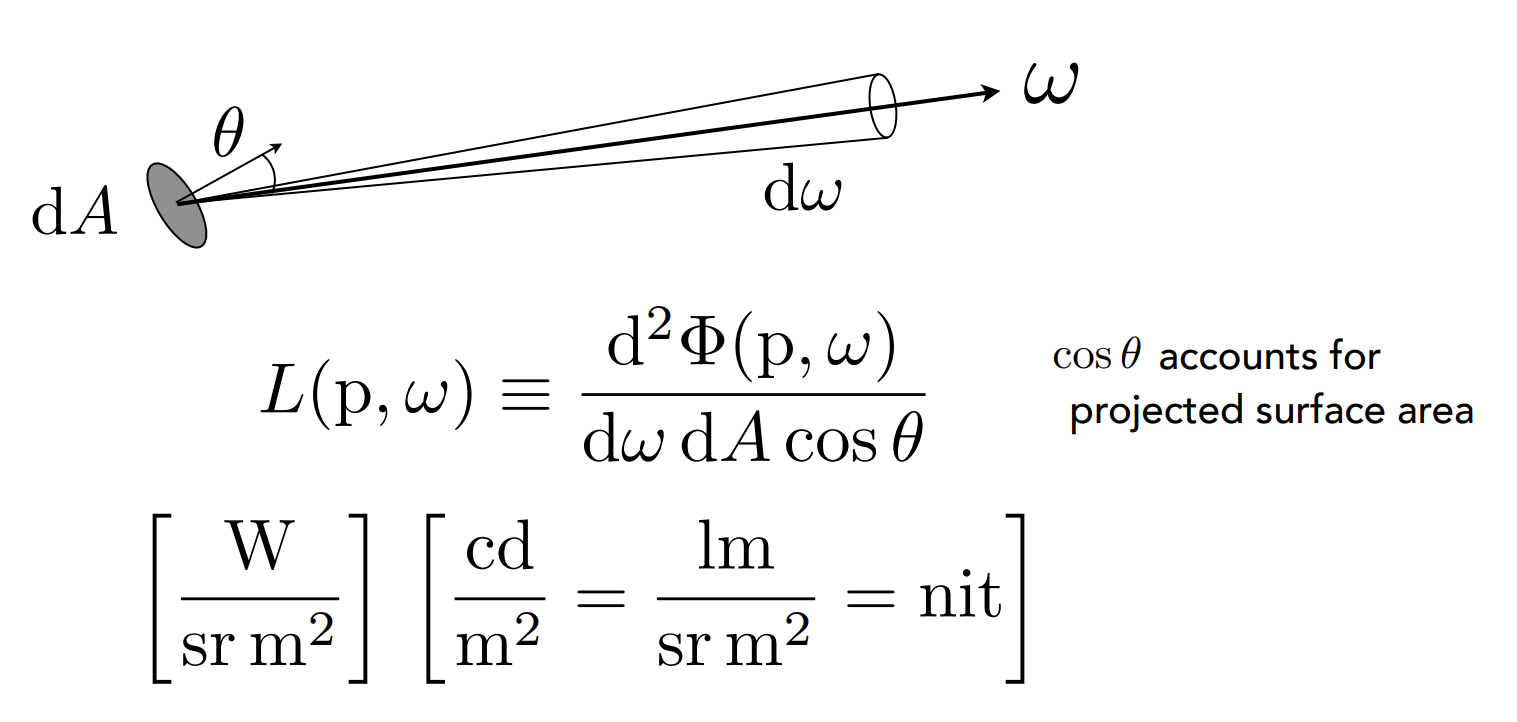
• 理解：

  • Radiance定义：power per unit solid angle, per projected unit area.

  • Irradiance: power per projected unit area

  • Intensity: power per solid angle

    • So:

      Radiance: Irradiance per solid angle

      ​ - Incident Radiance

      Radiance: Intensity per projected unit area

      ​ - Exiting Radiance

• Incident Radiance: The irradiance per unit solid angle arriving at the surface

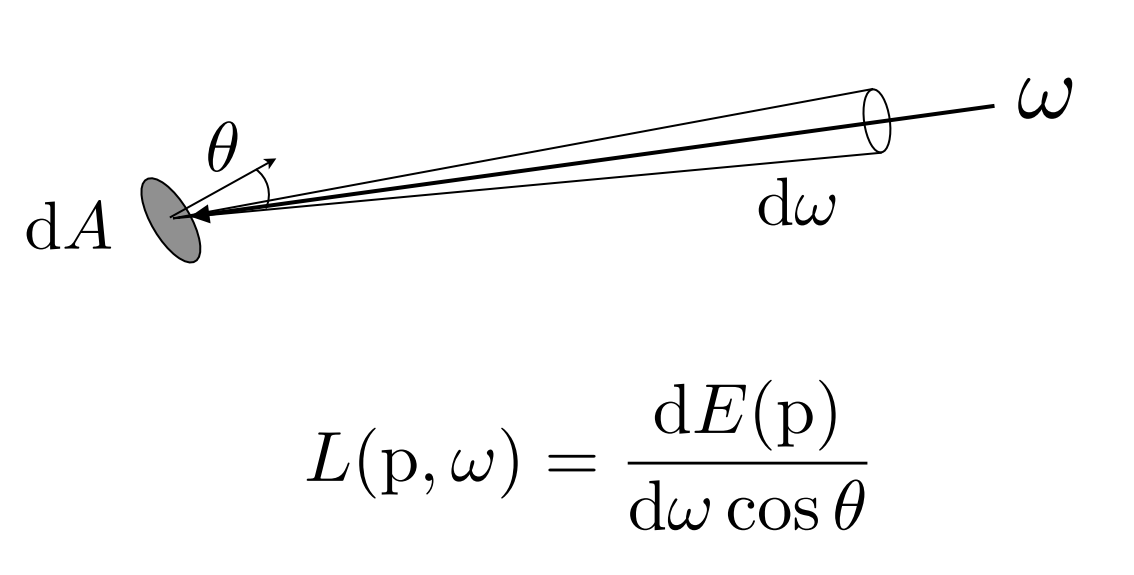
  • 即 $\omega$ 方向的光线对于 $dA$ 的贡献；
• Exiting Radiance: The intensity per unit projected area leaving the surface
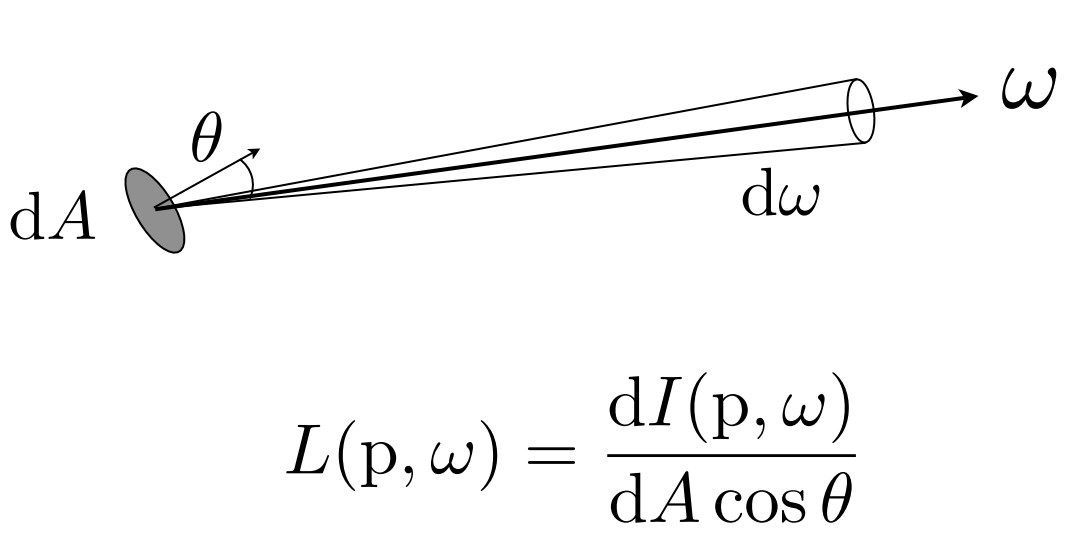
  • 即面积光 $dA$ ，对 $\omega$ 出射方向的贡献；
• Irradiance vs. Radiance
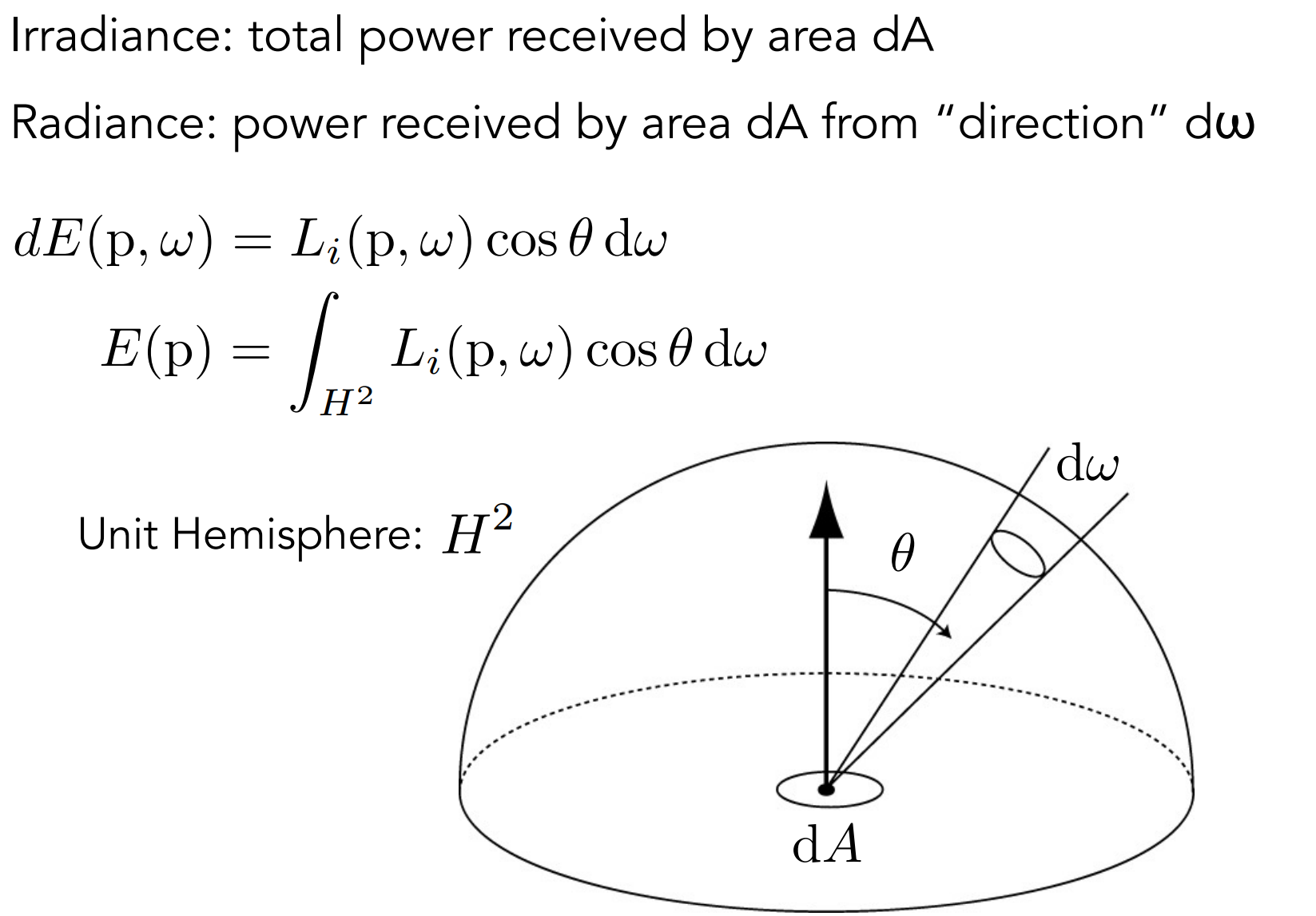
  • Irradiance和Radiance的区别在于方向性；
  • 图中，$dA$ 的辐照度 $E(p)$ 为各方向（半圆）对 $dA$ 的贡献。$dA$ 的Radiance $L_i(p,w)$ 为入射方向 $d\omega$ 对 $dA$ 的贡献；
  • 即，Irradiance $E(p)$ 是 radiance $L_i(p,w)$ 对于各个立体角的积分，$L_i(p,\omega)$ 是 $E(p)$ 方向 $\omega$ 的积分；

c). BRDF(Bidirectional Reflectance Distribution Function)

Ver Games101

• 过程：光线照射到一点（$p$），该点吸收能量，再辐射出去；
• 定义：
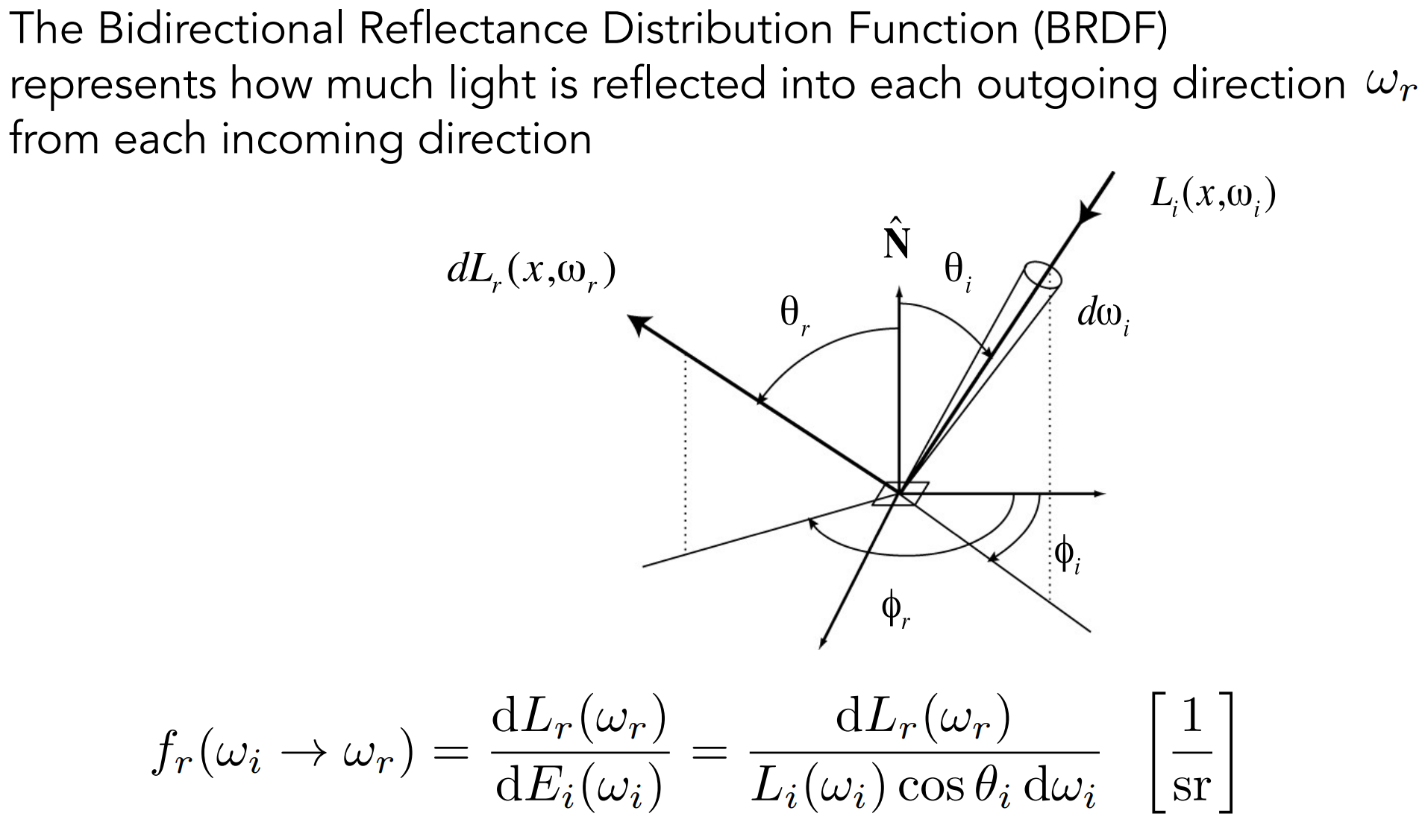
  • 分母：${\omega}_i$ 方向入射的radiance $L_i(x,{\omega}_i)$，被一点吸收后，辐射往各个方向的Irradiance $E_i({\omega}_i)$；
  • 分子：$E_i({\omega}_i)$，对 ${\omega}_r$ 方向radiance的贡献 $L_r(x,{\omega}_r)$

Ver self:

• 定义：BRDF（双向反射分布函数, bidirectional reflective distribution function）， 是指当一束光从某个方向( $\vec l$ )照射到某个点($p$)上时，在某个方向上( $\vec v$ )的出射辐射通量占总的入射辐射通量的比例

基于物理着色：BRDF - Maple的文章 - 知乎

关于brdf的两件小事 - Dua的文章 - 知乎

• 可以理解对于某一微小（对立体角）出射光线ωi，某一微小入射光线ωj对其radiance的贡献；

• 也可以理解成某一微小入射光线ωj，弹射到某一方向的微小立体角ωi的光线强度的比值；

• 由于为了方便测量，不定义为radiance相除（即如果按照我们一开始对入射方向 微分的方式定义brdf，那么科学家们只需要使用一个极小的光源从 方向入射到点p，就可以测得brdf的值。但是如果定义为radiance相除，就很难输入一个填充立体角刚好等于1的光源。)正常单位为：

  $${1\over{sr}}$$

d). Rendering equation

d.1). 简介

• The Reflection Equation
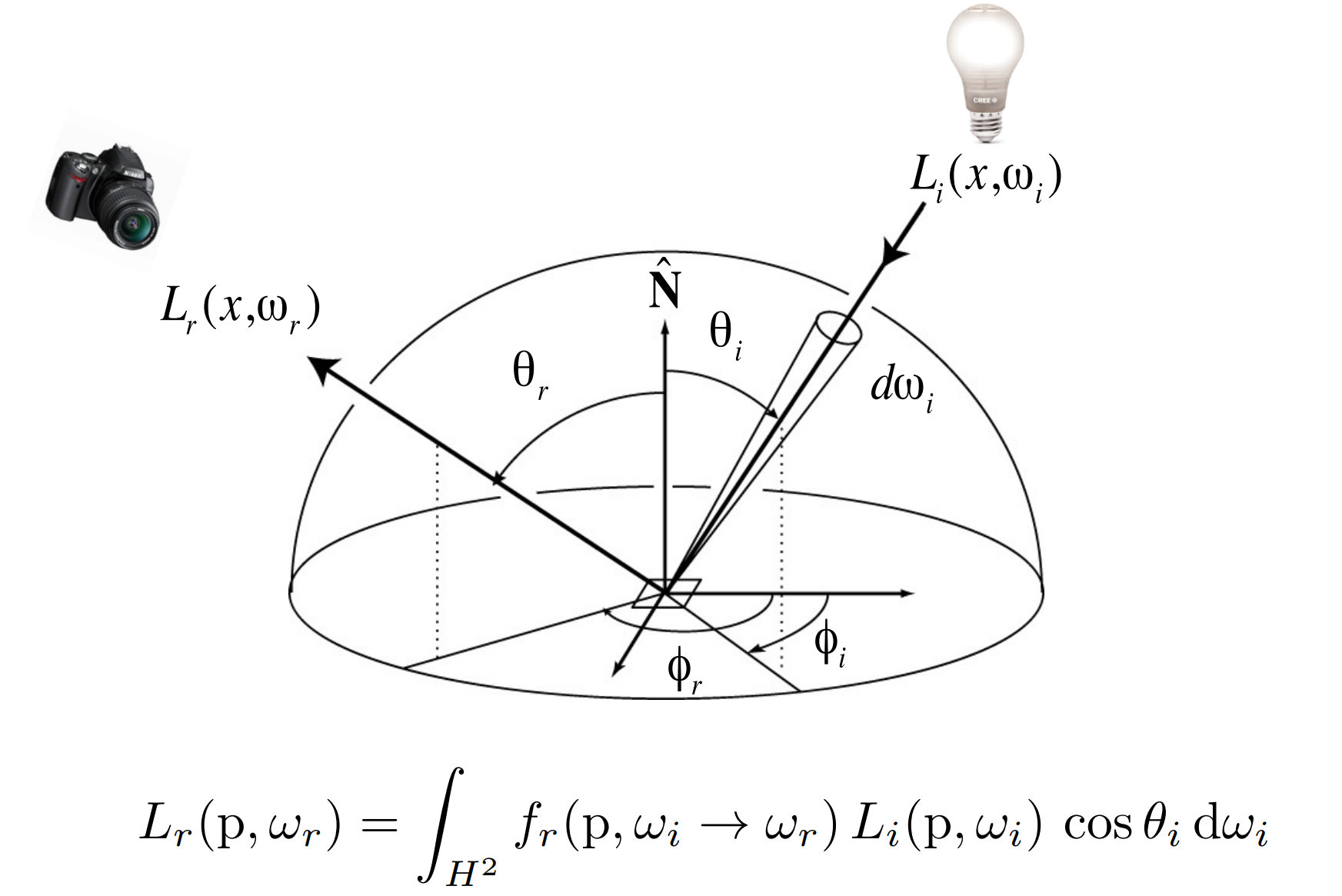
  • $f_r(p,w_i,w_r)$ 为该点的BRDF
• 
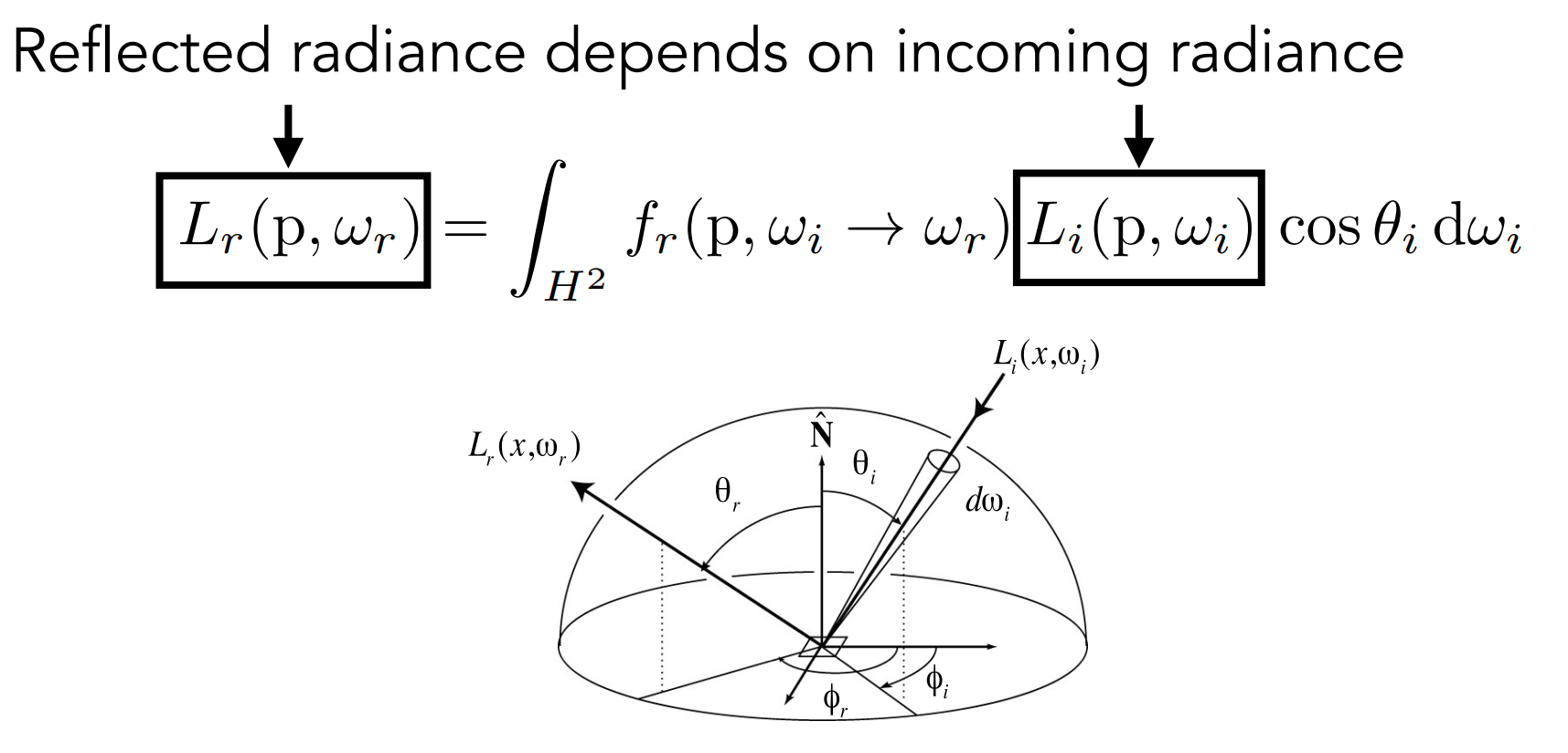
  • 问题：
    1. incoming radiance 不止来源于光源，也来源于其他反射（递归）；
    2. 未考虑自发光情况（加入自发光项，变为渲染方程）

• The Rendering Equation
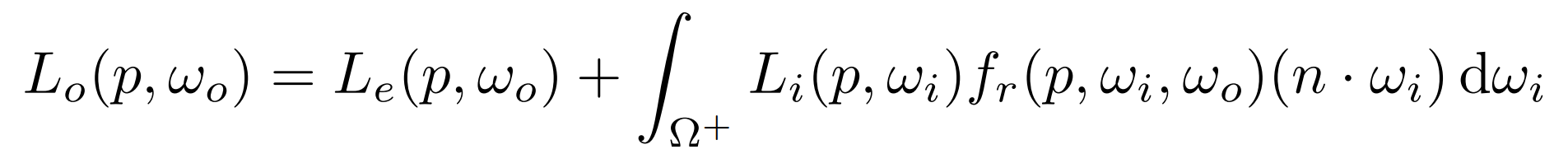
  • 加入了自发光项 $L_e(p,{\omega}_o)$
  • 考虑多次反射
  • 注意：该方程假定所有方向都是朝外的；
  • $H^2$ 和 $\Omega$ 表示半球的积分域；

d.2). 理解

• Reflection Equation:
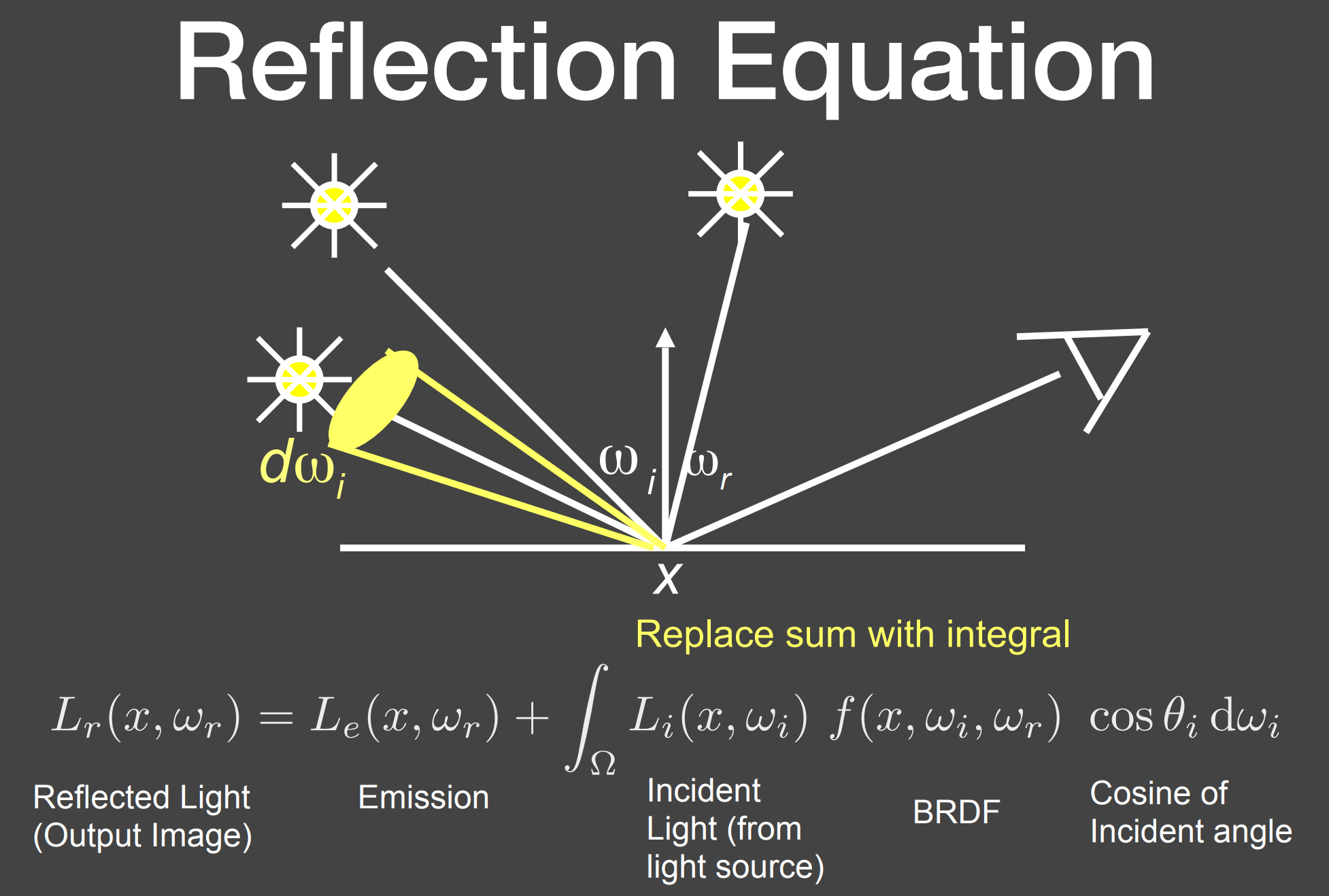
  • 反射的Radiance是各个方向光源对出射方向Radiance贡献的积分；
  • 未考虑光线多次弹射
• Rendering Equation:
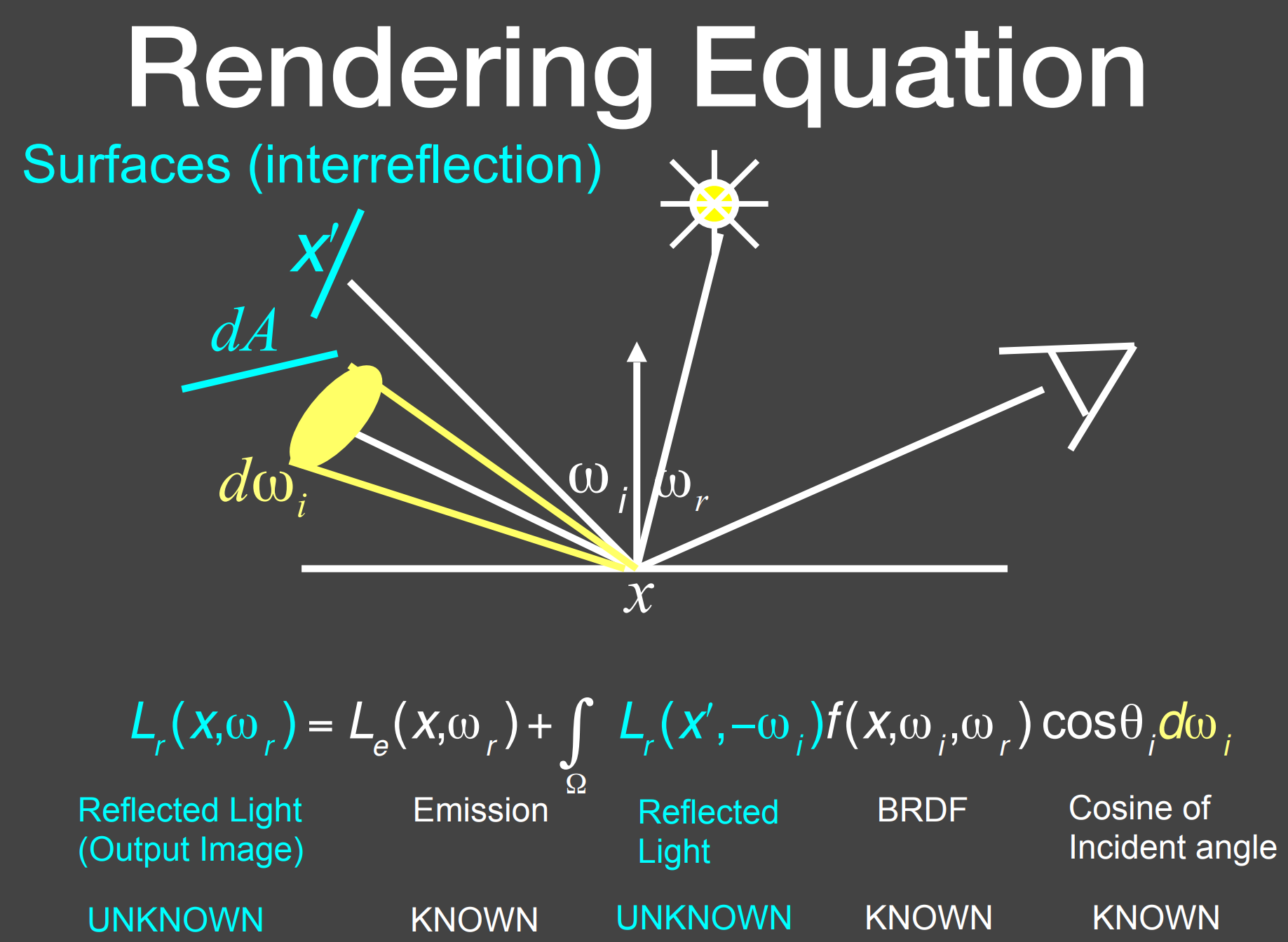
  • 考虑多次弹射，即其他物体反射的光线也会对出射方向 ${\omega}_r$ 的Radiance做出贡献；
  • 对于渲染方程，只有 $L_r(x,{\omega}_r)$ 和 $L_r(x’,-{\omega}_i)$ 是未知的；

• 简化渲染方程：
  • Rendering Equation as Integral Equation
  • Linear Operator Equation
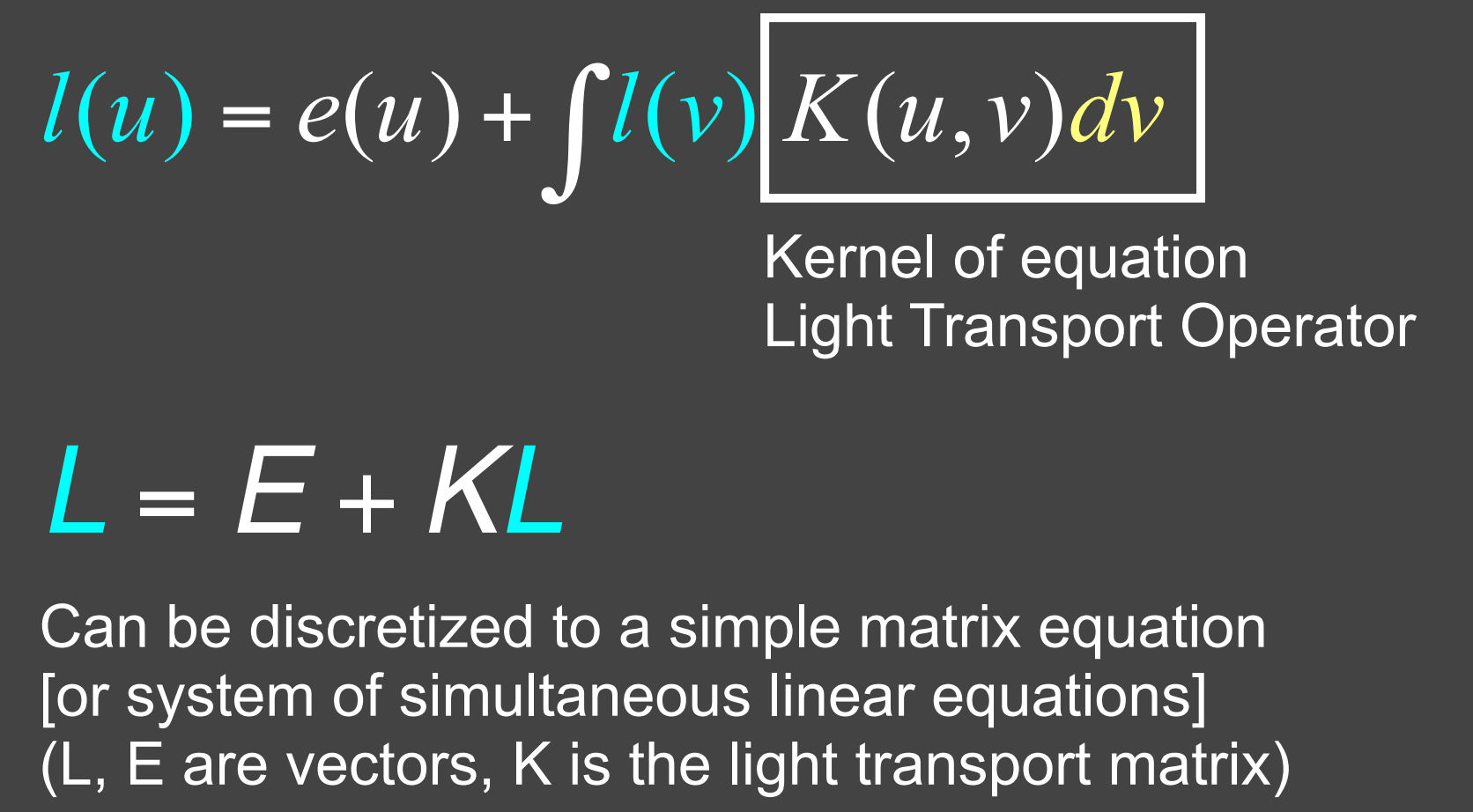
    • $E$ 环境中自发光对应向量，$L$ Radiance对应的向量；
    • $K$ 反射算子（矩阵）
• 对于Rendering Equation的线性形式，我们可以用以下式子逼近（类似泰勒展开）：

• Rendering Equation的线性形式对于光追的启示：

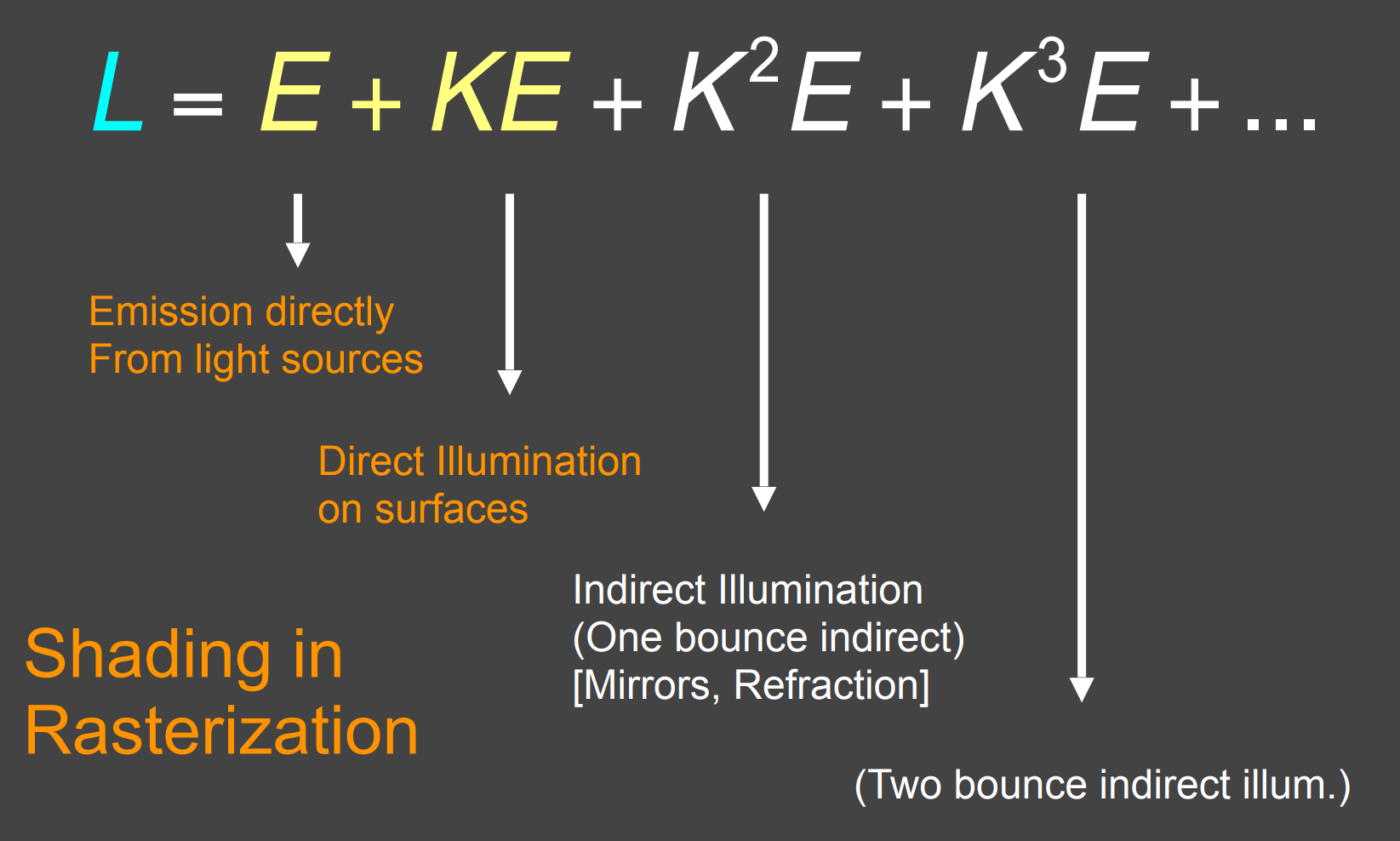
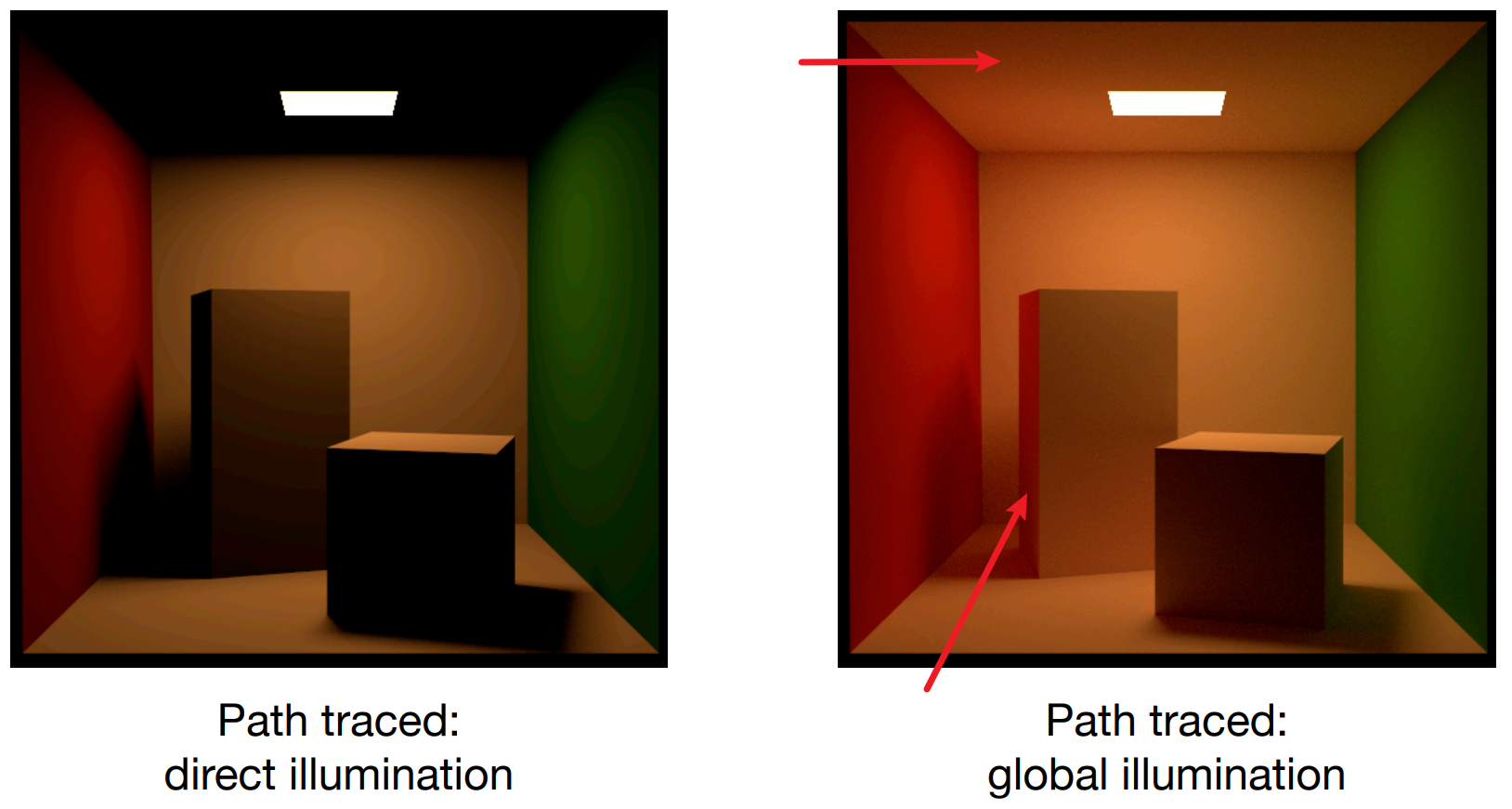
  • $E$ 为自发光，$KE$ 为 直接光照（即弹射一次），$K^2E$ 为间接光照（弹射两次）
  • 全局光照（Global illumination, GI）：直接光照+间接光照
  • 基础的光栅化只做了自发光和直接光照，即 $E$ 和 $KE$

• 对比

  
  
  • 上方玻璃灯：两次弹射时，光线从摄影机出发不能从玻璃罩中射出，因此其为黑色。而四次弹射时，光线从摄影机出发可以从玻璃罩中射出；
  • 当bounce数目增大时，亮度会趋于一个值，而不会无限增大；

e). Probability

Lecture 16 Ray Tracing 4 (Monte Carlo Path Tracing)

a). Monte Carlo Integration

• 使用原因：一些函数过于复杂，因此对于特定积分域，不求不定积分，只求其积分的结果。（一种数值方法）

• 过程：对函数的随机样本进行平均来估计函数的数值；

  

  • 

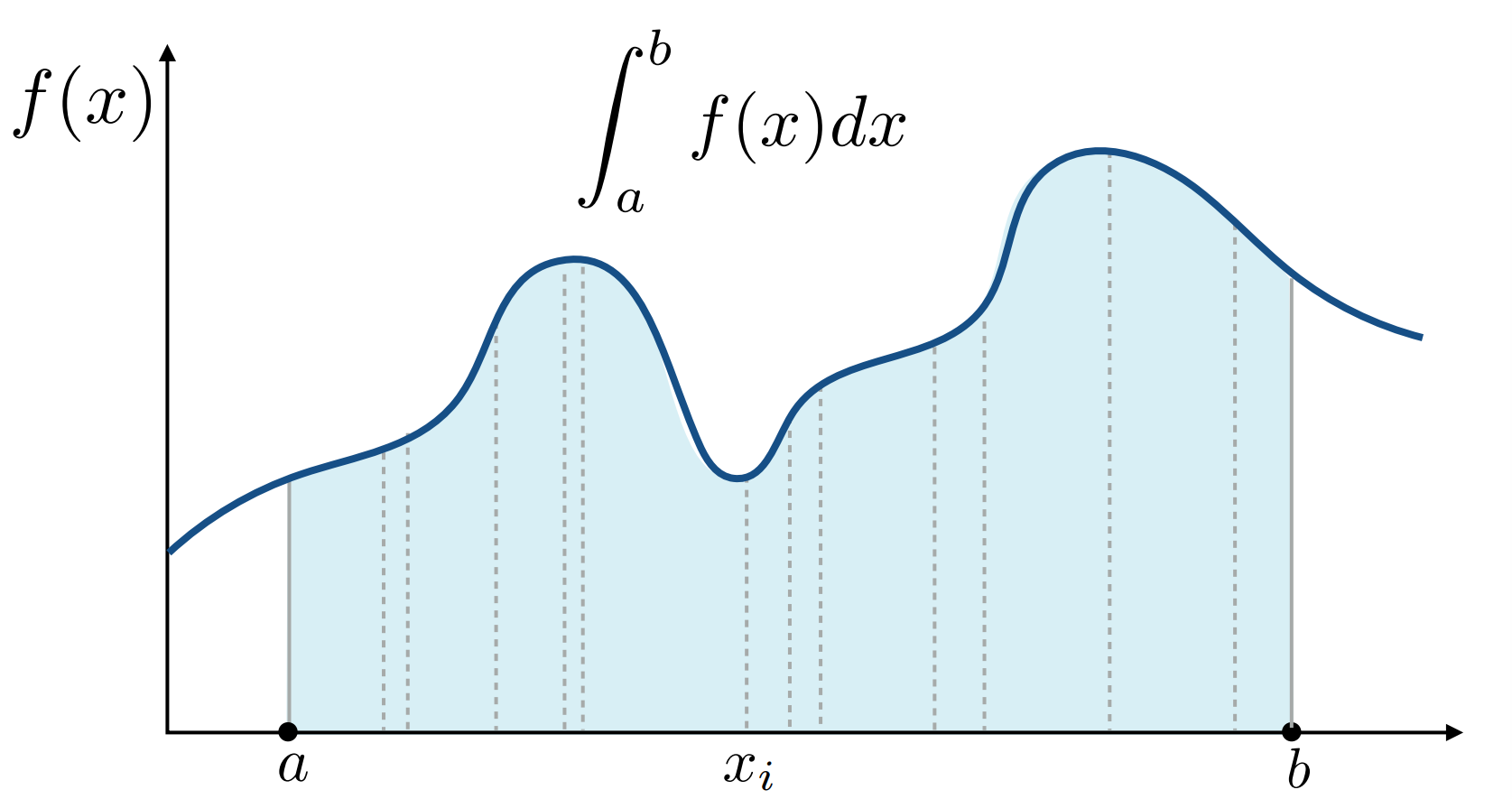
    • 除以 $p(x_i)$ 是一种加权，因为对于积分域上样本的采样可能是不均匀随机采样

  • 均匀采样的情况：

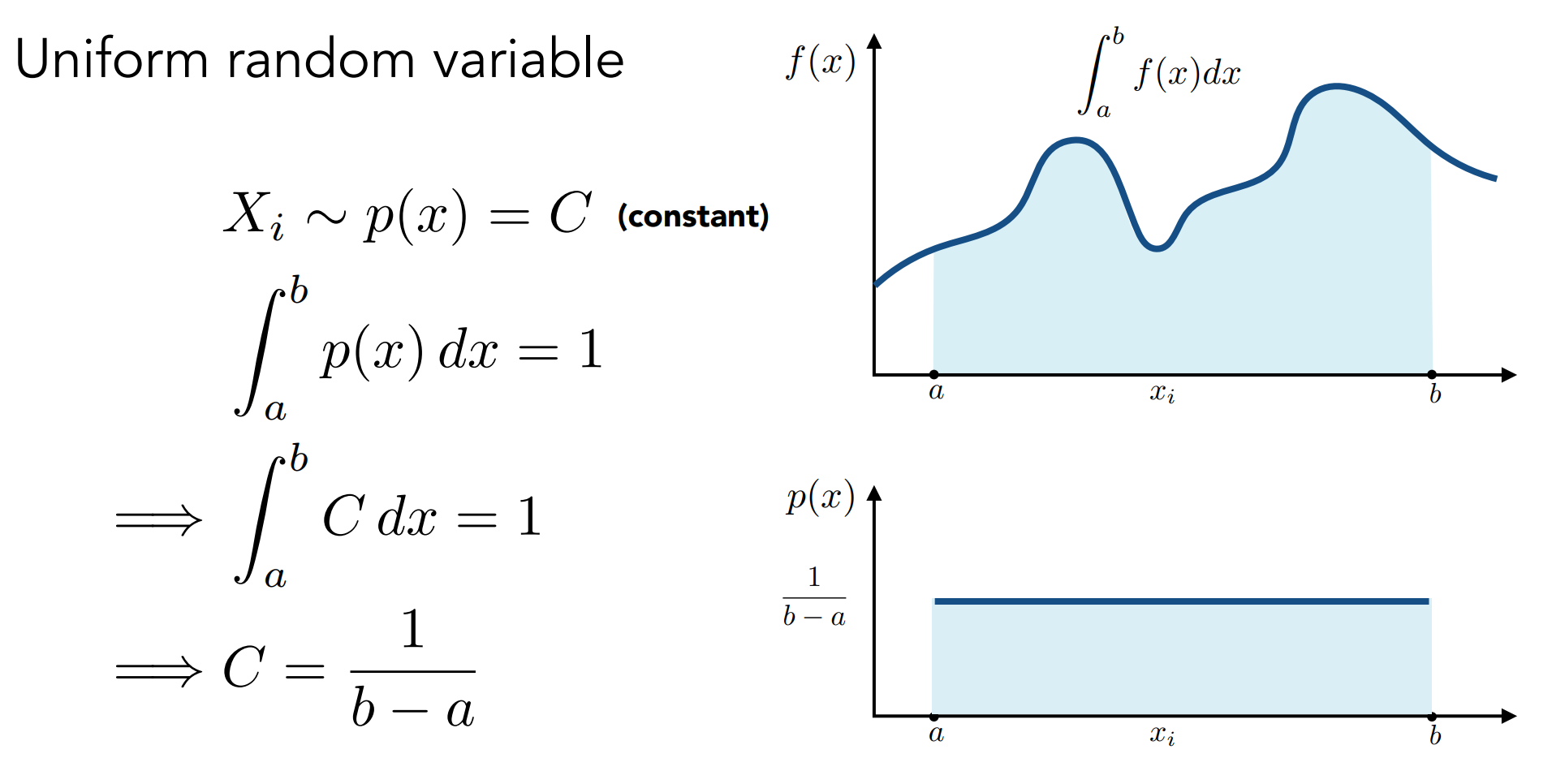
  • Some notes：

    1. 采样越多，方差越小
    2. 如在$x$上积分，要采样$x$

b). Paht Tracing

b.1). vs Whitted-Style Ray Tracing

• Whitted-Style Ray Tracing

  • 遇到光滑物体会只会 反射/折射（择一进行）

    • 无法表现Glossy reflection

      

  • 遇到漫反射物体停止弹射

    • 没有Color Blooding(eg.direct illumination)，考虑不到漫反射物体之间的光线传播

    

• But the rendering equation is correct

  $$L_{o}\left(p, \omega_{o}\right)=L_{e}\left(p, \omega_{o}\right)+\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i}$$
  • 需要做的：
    1. 解决半球域的定积分
       • 蒙特卡洛积分
    2. 递归

b.2). A Simple Monte Carlo Solution(Direct illumination)

• 渲染一个Pixel（Point），当前 之考虑直接光照

  

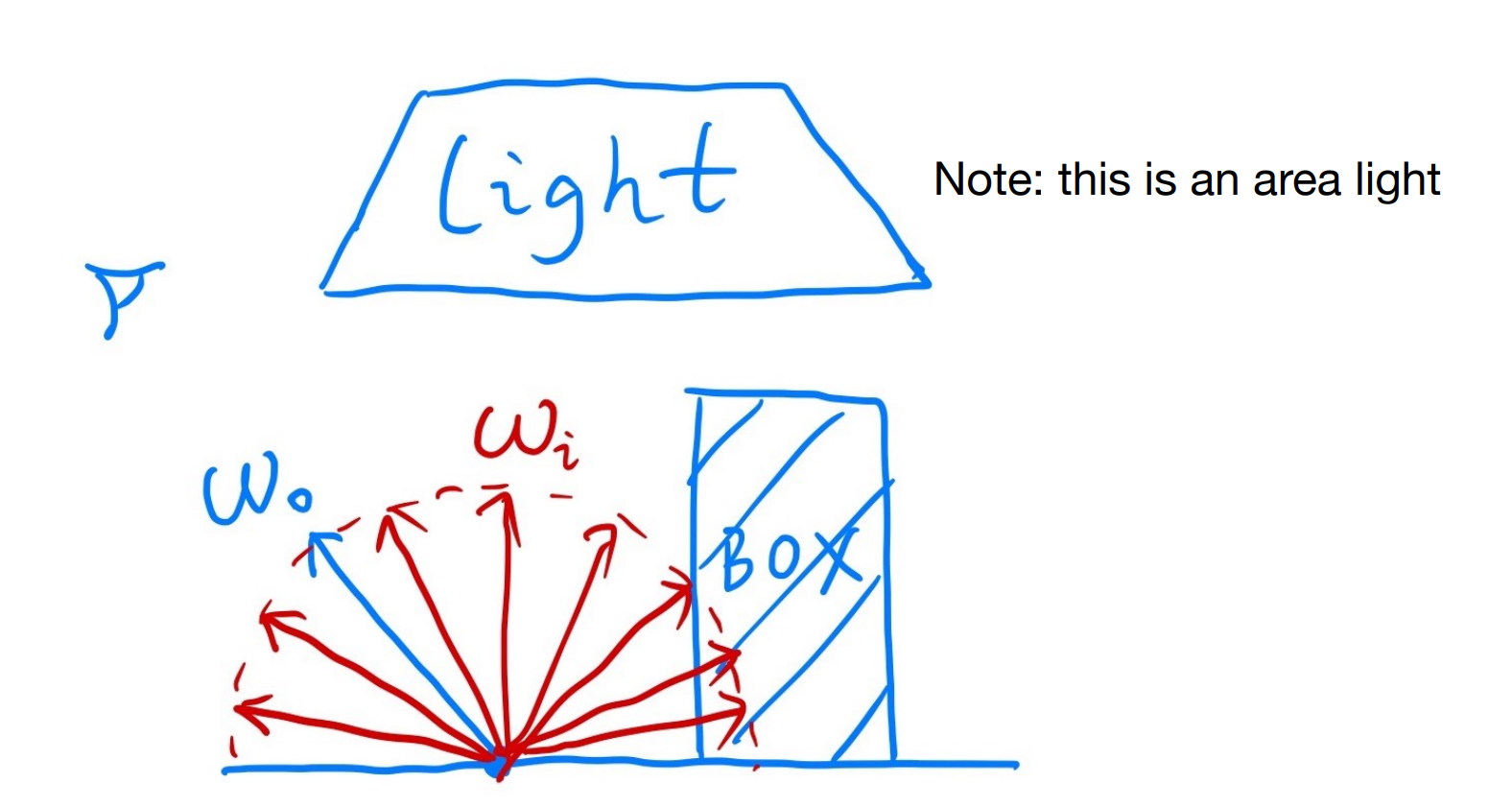
  • 当 $\omega_i$ 与light相交时，计算该方向的radiance；与Box相交时，则该方向的radiance=0；

• P-Code

  

b.3). Global illumination(加入递归)

b.3.1). GI and problems

• P-Code

  

  • Problem1: Explosion of #rays as #bounces go up

    

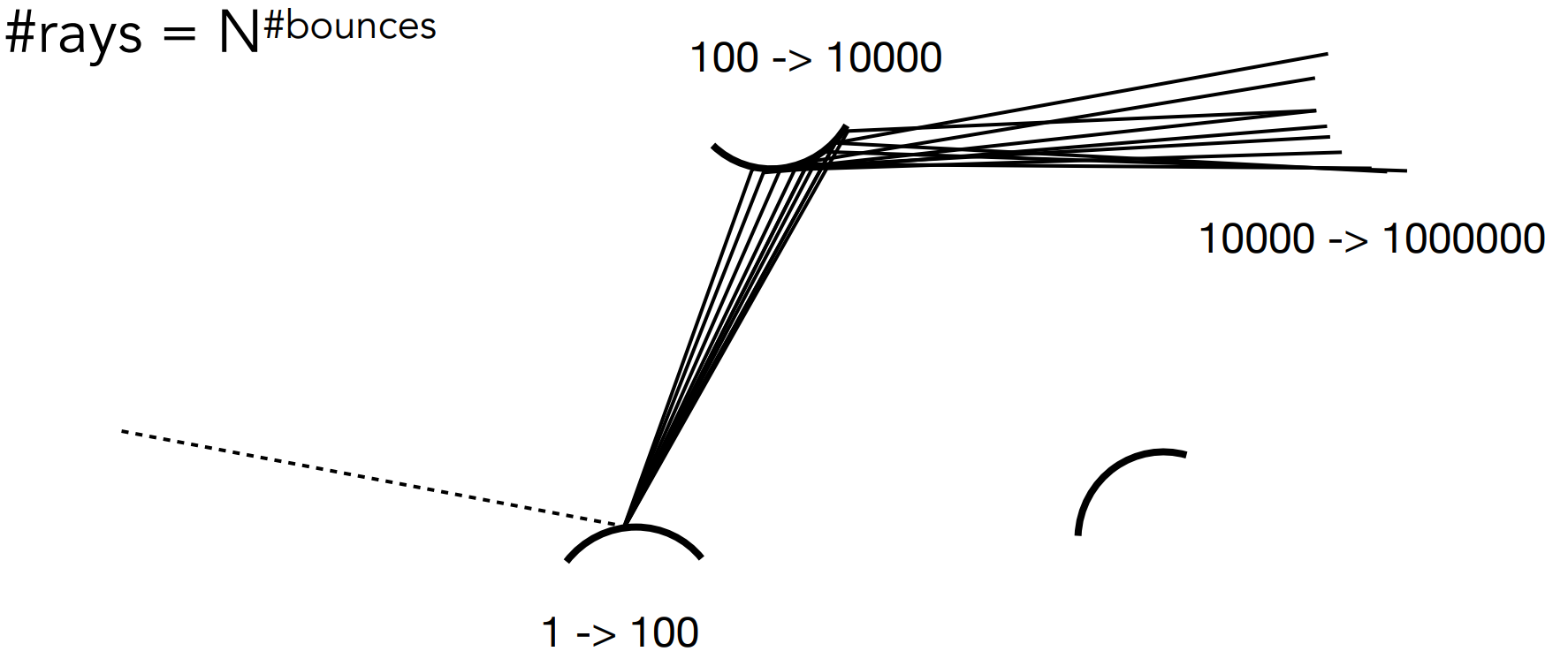
    • 解决方法： N=1（N=1即Path Tracing，Distributed Ray Tracing if N != 1）

      • N=1会造成较多的Noise，因此采用Subpixel，即每个像素内多次采样（Samples per pixel, SPP）

        

  • Problem2: 递归不会停止

    • 现实世界中，光线的弹射次数是无限的

    • 简单地，减少弹射次数 == 减少能量；

    • 解决方法： Russian Roulette(RR, 俄罗斯轮盘赌)

b.3.2). Russian Roulette(RR, 俄罗斯轮盘赌)

• 先前一点的着色结果是 $L_o$，引入RR后

  • With probability $P$, shoot a ray and return the shading result divided by P: Lo / P
  • With probability $1-P$, don’t shoot a ray and you’ll get 0

• 由此可得出数学期望 $E=P \cdot\left(\frac{L_{o}}{p}\right)+(1-P) \cdot 0=L_{o}$

  

b.3.3). 优化

• 计算直接光照时，如对点P向各个方向均匀采样，当光源小时，直接光照的贡献会小，造成较多的噪声；

  

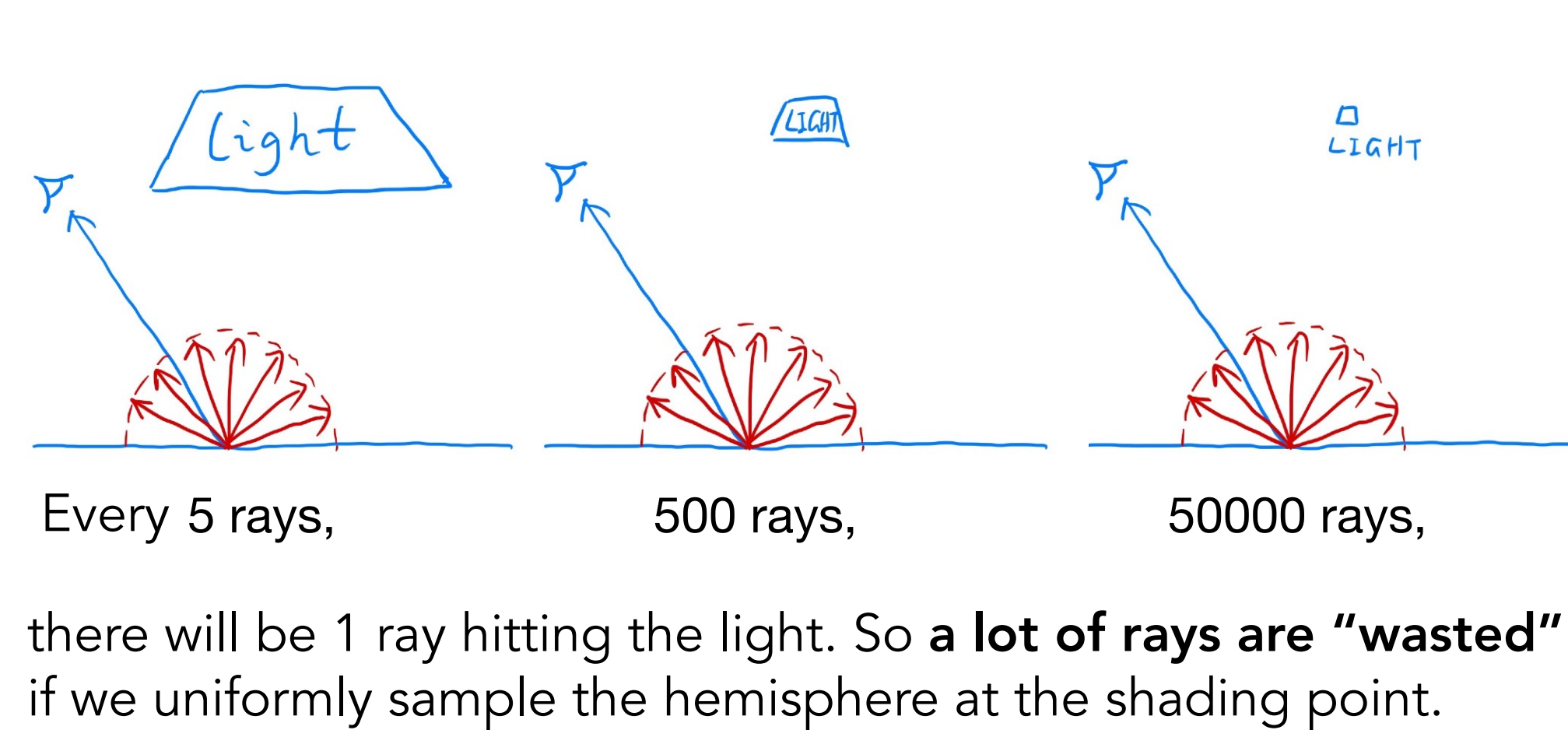
• 解决方法： 换元，使渲染方程对光源面积 $A$ 进行积分，pdf = 1/A

  

  $$d \omega=\frac{d A \cos \theta^{\prime}}{\left\|x^{\prime}-x\right\|^{2}} (Note: \theta^{\prime} , not \theta )$$
  • 立体角可以看前面辐射度量学的部分

• 

• 过程：（直接光照，间接光照分开计算）

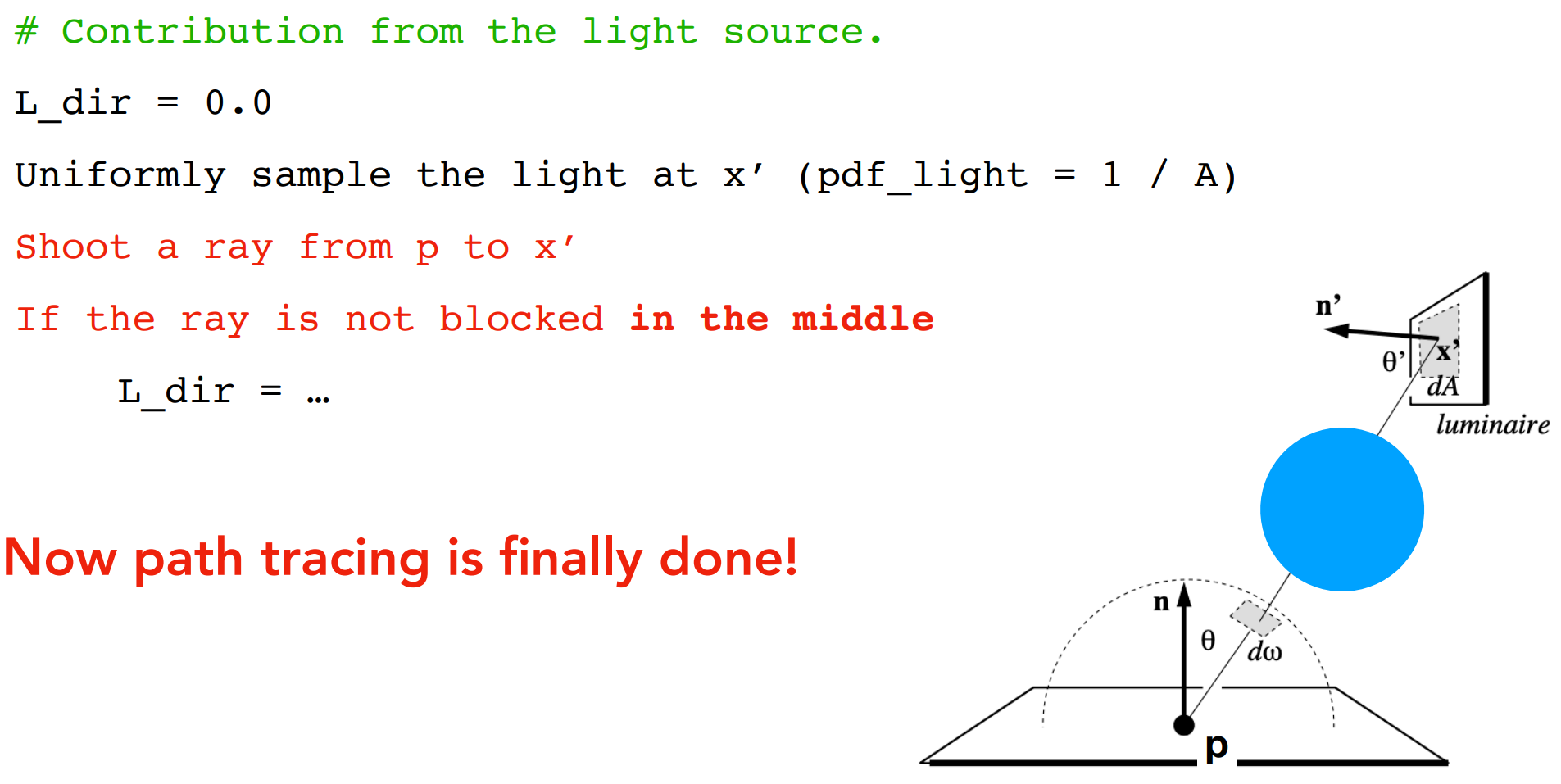
  1. light source (direct, no need to have RR)
  2. other reflectors (indirect, ues RR)

• P-Code（未考虑遮挡）

  

• 遮挡

---

附上上学期做的光追（借鉴smallpt）：

/**
* 采用Monte Carlo Path Tracing
* 漫反射采用的是Lambert
* 定义了三角面片和球体，其中三角面片可多片合成一个对象，
* 与三角面片求交则使用克拉默法则，而基于此做条件上的修改就可构建平行四边形，因此将平行四边形也归入三角面片
* 用平行四边形代替两个三角面片在适用且数量较多的情况下可显著提高运算效率
* 球体求交运算量小于三角面片，因此墙壁通过大半径的球体构建
*
* 由于想要表现出计算过程，许多数学运算未化简，运算效率不高
* 由于未使用BVH等方式约束，三角面片较为影响性能
* 目前场景除墙面外中有两个球体（镜面反射以及玻璃），以及一个立方体，通过6个三角面片（平行四边形）构成
*
* 由于为了提高运算效率，本程序中使用的蒙特卡洛采样方向约束在朝向其他对象的方向（射线在必定与其他对象相交的范围内随机），
* 但三角面片的约束范围较复杂，因此不支持将三角面片定义为光源
*
* 虽会增加噪声，为了运算效率，除了最大迭代次数，还引入经处理可使radiance的数学期望与原值相同的Russian Roulette，开始RR的次数为最大迭代次数除以2
* 
* 由于运算量大，采样默认设置为1，如想提高运行效率可删除掉三角面片
* 
* 绘制通过glut
* 程序输出为ppm格式图片
**/
#define _CRT_SECURE_NO_WARNINGS

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <iostream>
#include <iomanip>
#include <gl/glut.h>

#define DEPTH_MAX 10	//最大迭代次数
#define WIDTH 512
#define HIGHT 385

double M_PI = 3.1415926535;

double erand48(unsigned short xsubi[3]) {
	return (double)rand() / (double)RAND_MAX;
}

struct Vec {
	double x, y, z;
	Vec(double _x = 0, double _y = 0, double _z = 0) { x = _x; y = _y; z = _z; };

	Vec operator+(const Vec& b) const { return Vec(x + b.x, y + b.y, z + b.z); };	//加

	Vec operator-(const Vec& b) const { return Vec(x - b.x, y - b.y, z - b.z); }	//减

	Vec operator*(double b) const { return Vec(x * b, y * b, z * b); };	//数乘

	Vec mult(const Vec& b) const { return Vec(x * b.x, y * b.y, z * b.z); }	//数乘

	Vec& norm() { return *this = *this * (1 / sqrt(x * x + y * y + z * z)); }	//单位向量

	double dot(const Vec& b) const { return x * b.x + y * b.y + z * b.z; }	//点乘

	Vec cross(const Vec& b) const { return Vec(y * b.z - z * b.y, z * b.x - x * b.z, x * b.y - y * b.x); }	//叉乘
};

struct Ray {
	Vec o, d;
	Ray(Vec _o, Vec _d) : o(_o), d(_d) {};
};

enum Refl_t {	//反射类型
	DIFF,
	SPEC,
	REFR
};
struct MeshTriangle {	// 三角面片
	const Vec* verts;	// 顶点
	const int* vertsIndex;	//顶点排序
	const int numTris;	// 三角形数量
	Vec* vertices;
	Vec e, c;	// emission, color
	Refl_t refl;
	int isTriangle;

	//顶点， 顶点列表（决定构建顺序以及法线正负）， 三角面片数量， emission, color， 材质， 是否是三角形（或平行四边形）
	MeshTriangle(const Vec* _verts, const int* _vertsIndex, const int _numTris, Vec _e, Vec _c, Refl_t _refl, int _isTriangle = 1) :
		verts(_verts), vertsIndex(_vertsIndex), numTris(_numTris), e(_e), c(_c), refl(_refl), isTriangle(_isTriangle)
	{
		vertices = new Vec[3 * numTris];
		for (int i = 0; i < numTris; i++) {
			for (int n = 0; n < 3; n++) {
				vertices[3 * i + n] = verts[vertsIndex[3 * i + n]];
			}
		}
	}

	void move(int x, int y, int z) {	// 方便调试
		for (int i = 0; i < 3 * numTris; i++) {
			vertices[i] = vertices[i] + Vec(x, y, z);
		}
	}

	double intersect(const Ray& r, Vec& n) const {	// n返回法线
		double tnear = 1e20;
		double tnear_out;
		//std::cout << numTris << std::endl;	//
		Vec temp_normal;
		double temp = 1e20;
		bool flag = false;
		for (int i = 0; i < numTris; i++) {
			Vec& v0 = vertices[3 * i];
			Vec& v1 = vertices[3 * i + 1];
			Vec& v2 = vertices[3 * i + 2];
			/*std::cout << "x:" << v0.x << "y:" << v0.y << ", z:" << v0.z << std::endl;
			std::cout << "x:" << v1.x << "y:" << v1.y << ", z:" << v1.z << std::endl;
			std::cout << "x:" << v2.x << "y:" << v2.y << ", z:" << v2.z << std::endl;*/
			Vec E1 = v1 - v0;
			Vec E2 = v2 - v0;

			n = E1.cross(E2).norm();	//三角形法线
			Vec S = r.o - v0;
			Vec S1 = (r.d).cross(E2);
			Vec S2 = S.cross(E1);
			//tnear为时间 沿着三角形方向 t的为正
			//u,v 为重心坐标前的参数 都得为非负的还得小于1
			double S1E1 = S1.dot(E1);

			tnear = 1.0f / S1E1 * S2.dot(E2);
			double u = 1.0f / S1E1 * S1.dot(S);
			double v = 1.0f / S1E1 * S2.dot(r.d);
			double k = 1 - u - v;

			bool judge;
			if (isTriangle) {
				judge = tnear > 0 && v >= 0 && v <= 1 && u >= 0 && u <= 1 && k >= 0;
			}
			else {
				judge = tnear > 0 && v >= 0 && v <= 1 && u >= 0 && u <= 1;
			}

			if (judge) {	//不加k >= 0 可构建平行四边形
				if (!flag) {
					tnear_out = tnear;
					temp_normal = n;
					flag = true;
				}

				if (tnear < tnear_out) {
					tnear_out = tnear;
					temp_normal = n;
				}
			}
		}

		if (flag) {
			n = temp_normal;

			//std::cout << tnear_out << std::endl;
			return (tnear_out < 1e20 && tnear_out > 0) ? tnear_out : 0;
		}
		else {
			return 0;
		}

	}

	~MeshTriangle() {
		delete[] vertices;
	}
};

struct Sphere {
	double rad;	// radius
	Vec p, e, c;	// position, emission, color
	Refl_t refl;

	Sphere(double _rad, Vec _p, Vec _e, Vec _c, Refl_t _refl) :
		rad(_rad), p(_p), e(_e), c(_c), refl(_refl) {}

	double intersect(const Ray& r) const {
		Vec op = p - r.o;
		double t, eps = 1e-4;
		double b_12 = op.dot(r.d);		// -b / 2
		double det_14 = b_12 * b_12 - op.dot(op) + rad * rad;	// det / 4
		double det_14_sqrt = sqrt(det_14);
		return (t = b_12 - det_14_sqrt) > eps ? t : ((t = b_12 + det_14_sqrt) > eps ? t : 0);
		//if (det_14 < 0) {
		//	return 0;
		//}
		//else {
		//	t = b_12 - det_14_sqrt;
		//	if (t > eps) return t;	//考虑到浮点数的缺陷

		//	t = b_12 + det_14_sqrt;
		//	if (t > eps) return t;

		//	return 0;	//交点为反向延长线，不考虑
		//}
	}
};

Sphere spheres[] = {//Scene: radius, position, emission, color, material
	Sphere(1e5, Vec(1e5 + 1,40.8,81.6),  Vec(),Vec(.75,.25,.25),DIFF),//Left
	Sphere(1e5, Vec(-1e5 + 99,40.8,81.6),Vec(),Vec(.25,.25,.75),DIFF),//Rght
	Sphere(1e5, Vec(50,40.8, 1e5),       Vec(),Vec(.75,.75,.75),DIFF),//Back
	Sphere(1e5, Vec(50,40.8,-1e5 + 170), Vec(),Vec(.25,.25,.25), DIFF),//Frnt
	Sphere(1e5, Vec(50, 1e5, 81.6),      Vec(),Vec(.75,.75,.75),DIFF),//Botm
	Sphere(1e5, Vec(50,-1e5 + 81.6,81.6),Vec(),Vec(.75,.75,.75),DIFF),//Top
	Sphere(12,Vec(27,12.5,47),         Vec(),Vec(1,1,1) * .999, SPEC),//Mirr
	Sphere(16.5,Vec(73,16.5,78),         Vec(),Vec(1,1,1) * .999, REFR),//Glas
	Sphere(1.5, Vec(50,81.6 - 16.5,81.6),Vec(4,4,4) * 100,  Vec(), DIFF)  //Lite
};

Vec verts[8] = {	//vertices
	Vec(26, 0, 95),
	Vec(41, 0, 90),
	Vec(31, 0, 110),
	Vec(46, 0, 105),
	Vec(26, 40, 95),
	Vec(41, 40, 90),
	Vec(31, 40, 110),
	Vec(46, 40, 105),
};

int vertsIndex[18] = { 0, 4, 1,		// 顺序影响法线方向
					1, 5, 3,
					3, 7, 2,
					2, 6, 0,
					6, 7, 4,
					2, 0, 3,
};

//int vertsIndex[36] = { 0, 4, 1,		// 顺序影响法线方向
//					1, 4, 5,
//					1, 5, 7,
//					1, 7, 3,
//					3, 7, 6,
//					3, 6, 2,
//					2, 6, 0,
//					0, 6, 4,
//					6, 7, 4,
//					7, 5, 4,
//					2, 0, 3,
//					3, 0, 1,
//					};

MeshTriangle meshTriangles[] = {
	MeshTriangle(verts, vertsIndex, 6, Vec(), Vec(.25, .75, .25), DIFF, 0),
};	//vertices, vertsIndex, numTris, emission, color, material


int numSphere = sizeof(spheres) / sizeof(Sphere);
int numMeshTriangle = sizeof(meshTriangles) / sizeof(MeshTriangle);

inline double clamp01(double x) {	//截断到01
	return x < 0 ? 0 : (x > 1 ? 1 : x);
}

inline double gamma(double x, float n = 2.2) {
	return pow(clamp01(x), 1 / n);
}

inline int toInt255(double x) {	//gamma取2.2, 四舍五入
	return int(gamma(x) * 255 + .5);
}

inline void UpdateProgress(float progress)	//进度提醒
{
	int barWidth = 70;

	std::cout << "[";
	int pos = barWidth * progress;
	for (int i = 0; i < barWidth; ++i)
	{
		if (i < pos)
			std::cout << "=";
		else if (i == pos)
			std::cout << ">";
		else
			std::cout << " ";
	}

	//三位小数
	std::cout << "] " << std::setiosflags(std::ios::fixed) << std::setiosflags(std::ios::right) << std::setprecision(3) << float(progress * 100.0) << " %\r";
	std::cout.flush();
}

inline bool intersect(const Ray& r, double& t, int& id, Vec& normal) {	//t最短的相交, n 返回法线
	double n = sizeof(spheres) / sizeof(Sphere) + numMeshTriangle;
	double d;
	double inf = t = 1e20;
	for (int i = 0; i < n; i++) {
		//std::cout << i << std::endl;	//
		if (i < numSphere) {
			if ((d = spheres[i].intersect(r)) && d < t) {	// 注意：不自交（真坑啊。。。）
				t = d;
				id = i;
			}
		}
		else {
			d = meshTriangles[i - numSphere].intersect(r, normal);
			if (d && d < t) {
				//std::cout << d << std::endl;
				t = d;
				id = i;
			}
		}
	}
	return t < inf;
}

//Xi:随机种子	E：whether to include emissive color
Vec radiance(const Ray& r, int depth, unsigned short* Xi, int E = 1) {
	double t;	//与交点距离
	int id = 0;
	Vec temp_n;
	if (!intersect(r, t, id, temp_n)) {		//id >= numSphere说明是三角面片
		return Vec();	//miss
	}
	//std::cout << id << std::endl;	//

	Vec x = r.o + r.d * t;// Ray hit point
	Vec n;	//normal(射线经过obj内部后,n为负数)
	Vec f;
	Refl_t obj_refl;
	Vec obj_e;
	if (id < numSphere) {
		const Sphere& obj = spheres[id];
		n = (x - obj.p).norm();
		f = obj.c;
		obj_refl = obj.refl;
		obj_e = obj.e;
	}
	else {
		//std::cout << id << std::endl;
		//if (x.x == 36) std::cout << "x:" << x.x << "y:" << x.y << ", z:" << x.z << std::endl;
		const MeshTriangle& obj = meshTriangles[id - numSphere];
		n = temp_n.norm();
		f = obj.c;
		obj_refl = obj.refl;
		obj_e = obj.e;
	}

	if (depth > DEPTH_MAX) {

		return Vec();
	}
	//Vec n = (x - obj.p).norm();	// sphere normal(射线经过obj内部后,n为负数)
	Vec n_real = n.dot(r.d) < 0 ? n : n * -1;	//sphere normal
	//std::cout << "x:" << f.x << "y:" << f.y << ", z:" << f.z << std::endl;	//

	//用rgb最大值作为Russian Roulette不终止的概率p
	//RR适用因为p * Li * (1/p) + 0 * (1-p) = Li，即数学期望等于Li
	double p = f.x > f.y && f.x > f.z ? f.x : f.y > f.z ? f.y : f.z;

	if (++depth > int(DEPTH_MAX / 2) || !p) if (erand48(Xi) < p) f = f * (1.0 / p); else return obj_e * E;

	//std::cout << "miss" << std::endl;
	if (obj_refl == DIFF) {
		//std::cout << "DIFF" << std::endl;	//
		//采用Lambert，出射方向任意，以极坐标的方式构建随机弹射光线方向
		double r1 = 2 * M_PI * erand48(Xi);
		double r2 = erand48(Xi);
		double r2_sqrt = sqrt(r2);

		//标准正交系
		Vec w = n_real;
		Vec u = ((fabs(w.x) > 0.1 ? Vec(0, 1) : Vec(1)).cross(w)).norm();
		Vec v = w.cross(u);
		Vec d = (u * cos(r1) * r2_sqrt + v * sin(r1) * r2_sqrt + w * sqrt(1 - r2)).norm();	//Ray direction, 即path tracing， N=1的那条射线

		Vec e;
		for (int i = 0; i < numSphere; i++) {
			const Sphere& s = spheres[i];
			if ((s.e.x <= 0 && s.e.y <= 0 && s.e.z <= 0) || i >= numSphere) continue;	//skip no radiance

			Vec sw = s.p - x, su = ((fabs(sw.x) > 0.1 ? Vec(0, 1) : Vec(1)).cross(sw)).norm(), sv = sw.cross(su);

			//x发出射向id=i的范围内随机方向的采样射线
			double cos_a_max = sqrt(1 - s.rad * s.rad / (x - s.p).dot(x - s.p));
			double eps1 = erand48(Xi), eps2 = erand48(Xi);
			//double cos_a = 1 - eps1*(1. - cos_a_max);
			double cos_a = 1 - eps1 + eps1 * cos_a_max;
			double sin_a = sqrt(1 - cos_a * cos_a);
			double phi = 2 * M_PI * eps2;
			Vec l = su * cos(phi) * sin_a + sv * sin(phi) * sin_a + sw * cos_a;
			l.norm();

			// Note: 
			// 根据Monte Carlo Integration得到相应形式的渲染方程(反射率方程)
			// Lo(p,wo) = (1/N)*∑(i~n) {(Li(p,wi)*fr(p,wi,wo)*(n*wi)) / pdf}
			// Lo:入射radiance, p:单位半球球心, wo:入射方向（微小立体角）
			// N:取样数（光线数）, Li wi略
			// fr:BRDF, n:法线方向
			// pdf: 分布函数
			// 由于采用的是path tracing N取1, Lo(p,wo) = (Li(p,wi)*fr(p,wi,wo)*(n*wi)) / pdf
			// 当采用Lambert漫反射的BRDF可推导出为1/pi
			// 对半球均匀采样时，pdf=1/单位半圆面积，但射线的方向是在于法线的夹角最大是a_max, 采样的区域被限定
			// 球形对角度A(法线方向与某一点的夹角)积分， 得S = ſ 2 * pi * r*r sinA dA = abs(2 * pi * r * r * cosA), r=1
			// 易得pdf = 1 / 球部分表面积 = 1 / (2 * pi * r * r(1-cos_a_max)) = 1 / (2 * pi * (1-cos_a_max))
			// Lo(p,wo) = (Li(p,wi)*fr(p,wi,wo)*(n*wi)) / pdf = Li(p,wi) * (1 / pi) * cos_a * (2 * pi * (1 - cos_a_max))
			Vec temp1;
			if (intersect(Ray(x, l), t, id, temp1) && id == i) {
				double omega = 2 * M_PI * (1 - cos_a_max);
				e = e + f.mult(s.e * l.dot(n_real) * omega) * (1 / M_PI);
				//std::cout << e.x << std::endl;
			}
		}
		//std::cout << f.x << std::endl;
		return obj_e * E + e + f.mult(radiance(Ray(x, d), depth, Xi, 0));	//TEST:E暂时设置为0

	}
	else if (obj_refl == SPEC) {
		//std::cout << "SPEC" << std::endl;	//
		return obj_e + f.mult(radiance(Ray(x, r.d - n * 2 * n.dot(r.d)), depth, Xi));
	}
	else if (obj_refl == REFR) {
		//std::cout << "REFR" << std::endl;
		Ray reflRay(x, r.d - n * 2 * n.dot(r.d));
		bool into = n.dot(n_real) > 0;
		double nc = 1;//真空
		double nt = 1.5;//玻璃
		double nnt = into ? nc / nt : nt / nc;
		double ddn = r.d.dot(n_real);
		double cos2_t = 1 - nnt * nnt * (1 - ddn * ddn);	//2是平方

		if (cos2_t < 0) {	//没有折射，发生全反射
			return obj_e + f.mult(radiance(reflRay, depth, Xi));
		}

		Vec tdir = (r.d * nnt - n * ((into ? 1 : -1) * (ddn * nnt + sqrt(cos2_t)))).norm();
		//考虑到计算量，采用近似算法
		double a = nt - nc, b = nt + nc, R0 = a * a / (b * b), c = 1 - (into ? -ddn : tdir.dot(n));
		double Re = R0 + (1 - R0) * c * c * c * c * c, Tr = 1 - Re, P = 0.25 + 0.5 * Re, RP = Re / P, TP = Tr / (1 - P);

		if (depth > 2) {
			if (erand48(Xi) < P) {	// RR
				return obj_e + f.mult(radiance(reflRay, depth, Xi) * RP);
			}
			else {
				return obj_e + f.mult(radiance(Ray(x, tdir), depth, Xi) * TP);
			}
		}
		else {
			return obj_e + f.mult(radiance(reflRay, depth, Xi) * Re + radiance(Ray(x, tdir), depth, Xi) * Tr);
		}
	}
}

Vec* c = new Vec[WIDTH * HIGHT];	//图像缓存

void Initial(void)
{
	glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
	glMatrixMode(GL_PROJECTION);
	int width = glutGet(GLUT_WINDOW_WIDTH);
	int height = glutGet(GLUT_WINDOW_HEIGHT);
	gluOrtho2D(0.0, width, 0.0, height);
}

void myDisplay(void) {
	glClear(GL_COLOR_BUFFER_BIT);
	glPointSize(1);
	for (int y = 0; y < HIGHT; y++) {
		for (int x = 0; x < WIDTH; x++) {
			int n = (HIGHT - y - 1) * WIDTH + x;
			glColor3f(gamma(c[n].x), gamma(c[n].y), gamma(c[n].z));
			glBegin(GL_POINTS);
			glVertex2f(x, y);
			glEnd();
		}
	}

	glFlush();
}
	

int main(int argc, char* argv[]) {
	int w = WIDTH, h = HIGHT;
	int samples = 1;	//设置每subpixel采样数
	//设置 camera
	Ray cam(Vec(50, 52, 295.6), Vec(0, -0.042612, -1).norm());
	Vec cx = Vec(w * 0.5135 / h);	//视场角
	Vec cy = (cx.cross(cam.d)).norm() * 0.5135;

	Vec r;	//摄影机射线
	auto clock_start = clock();
#pragma omp parallel for schedule(dynamic, 1) private(i)

	meshTriangles[0].move(15, 0, 0);
	for (int y = 0; y < h; y++) {
		UpdateProgress((float)y / HIGHT);
		unsigned short Xi[3] = { 0, 0, y * y * y };
		//设置四个子像素
		for (unsigned short x = 0; x < w; x++) {
			for (int sy = 0, i = (h - y - 1) * w + x; sy < 2; sy++) {
				for (int sx = 0; sx < 2; sx++, r = Vec()) {
					for (int s = 0; s < samples; s++) {
						double r1 = 2 * erand48(Xi);
						double dx = r1 < 1 ? sqrt(r1) - 1 : 1 - sqrt(2 - r1);
						double r2 = 2 * erand48(Xi);
						//std::cout << r1 << " " << r2 << std::endl;
						double dy = r2 < 1 ? sqrt(r2) - 1 : 1 - sqrt(2 - r2);
						Vec sample_direct = cx * (((dx + 0.5 + sx) / 2 + x) / w - 0.5)
							+ cy * (((dy + 0.5 + sy) / 2 + y) / h - 0.5) + cam.d;

						//std::cout << r.x << std::endl;
						r = r + radiance(Ray(cam.o + sample_direct * 140, sample_direct.norm()), 0, Xi) * (1.0 / samples);
						//std::cout << "x:" << r.x << "y:" << r.y << ", z:" <<r.z << std::endl;	//
					}
					//std::cout << c[i].x << std::endl;	//
					c[i] = c[i] + Vec(clamp01(r.x), clamp01(r.y), clamp01(r.z)) * 0.25;
				}
			}
		}
	}

	FILE* f = fopen("test.ppm", "wb");
	fprintf(f, "P3\n%d %d\n%d\n", w, h, 255);
	for (int i = 0; i < w * h; i++) {
		fprintf(f, "%d %d %d ", toInt255(c[i].x), toInt255(c[i].y), toInt255(c[i].z));
	}
	fclose(f);
	
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
	glutInitWindowPosition(100, 100);
	glutInitWindowSize(w, h);
	glutCreateWindow("Path Tracing");

	Initial();
	glutDisplayFunc(&myDisplay);
	glutMainLoop();
	return 0;
}