Games101_21_22 Animation

Lecture 21 Animation

a). History

b). Keyframe

c). Physical Simualtion

c.1). Mass Spring System

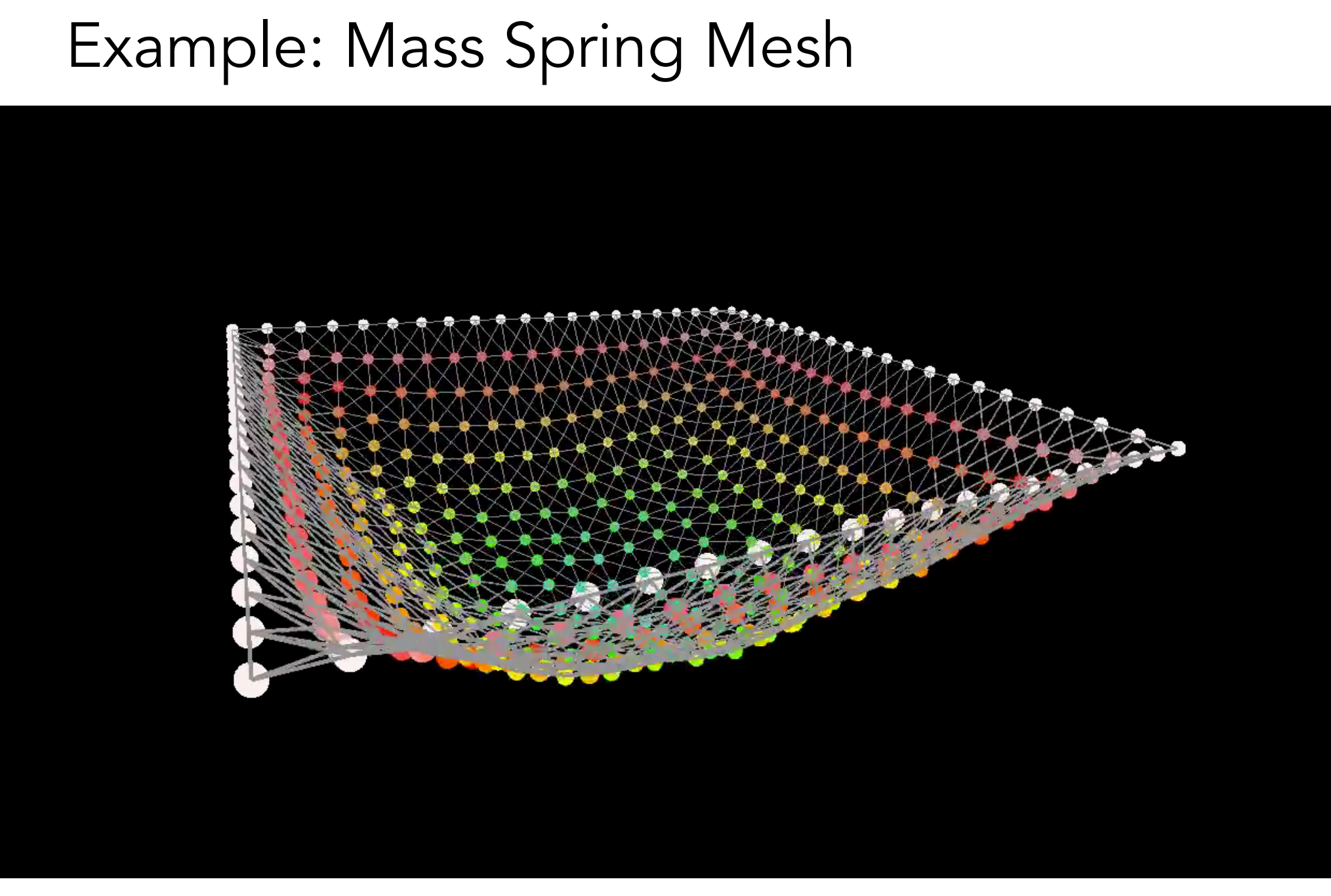
• Idealized spring

  

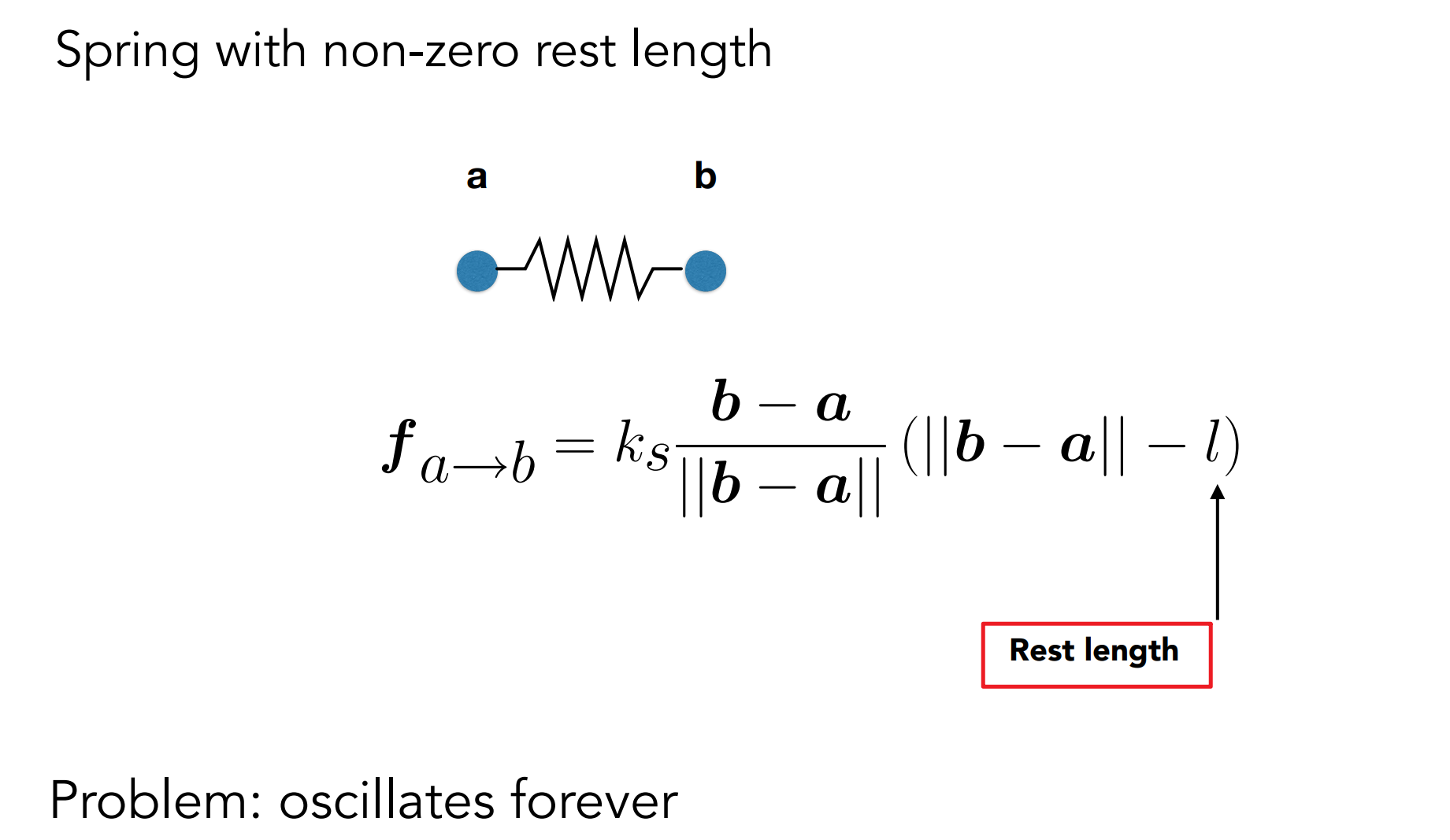
  • 但永远不会停止，因此加入摩擦力

---

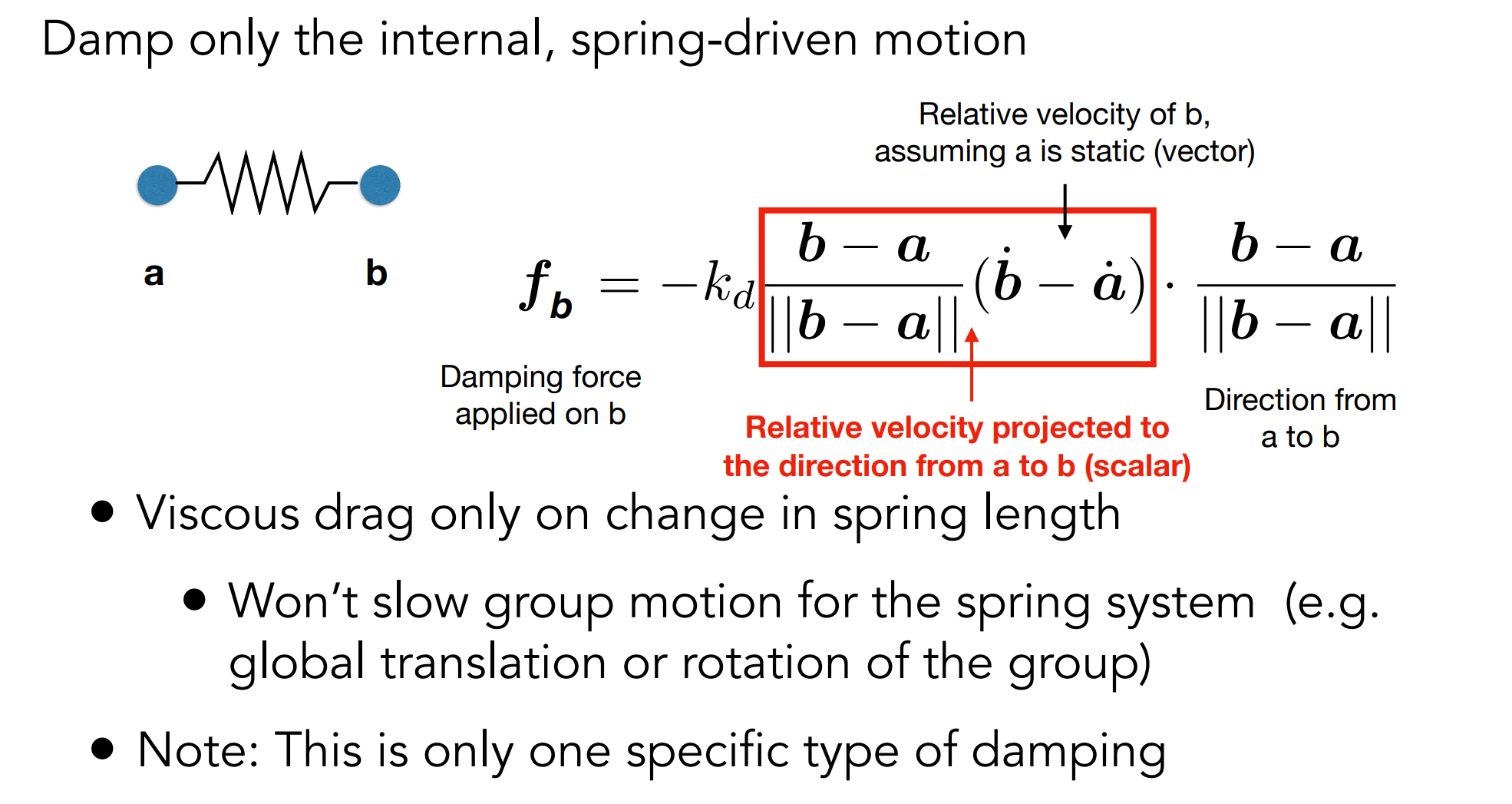
• 中间项为相对速度在向量$ab$方向的投影，因为（处于原长状态时）如果a点不动，b点绕a点做圆周运动，那$f_b=0$；

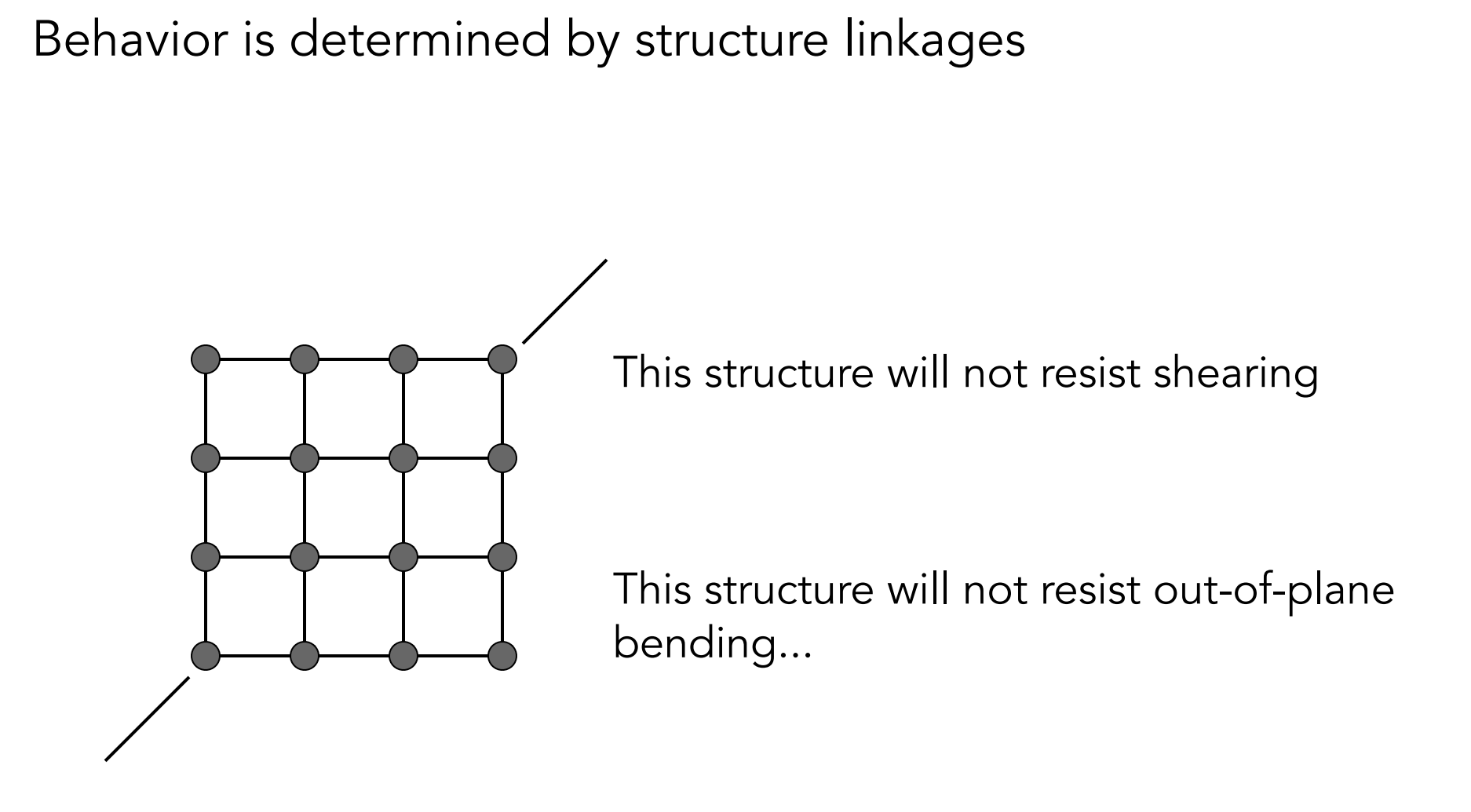
  • 但是无法表现剪切力（如对角线拉布，布基本形状不变）、弯曲力（out-of-plane，抗拒被像纸一样完全折叠为两个三角形）等

    

• 加入两条对角线，以及skip connection

  

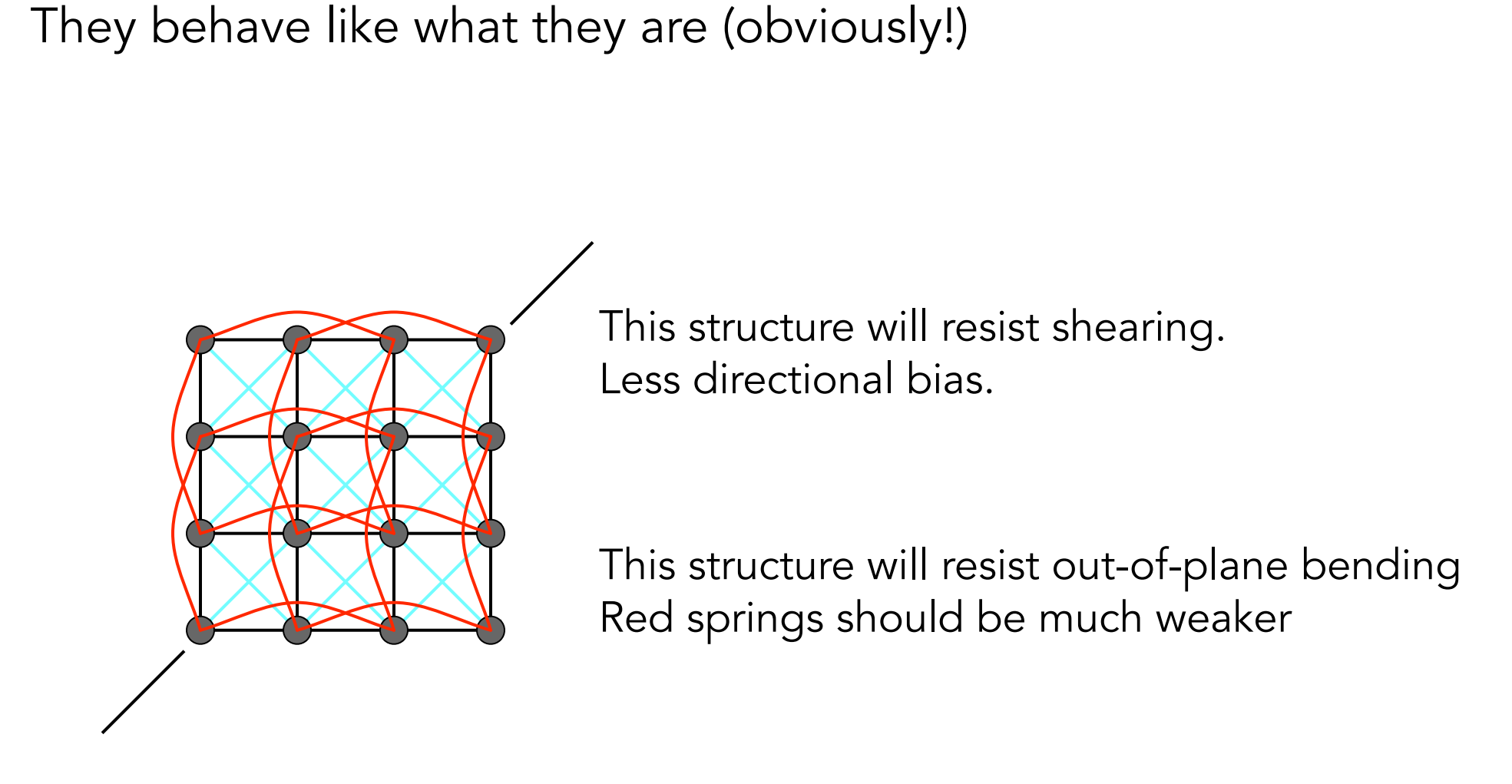
  • 红色较弱，仅其辅助作用；蓝色较强，其主要作用；

• 其他方式：FEM (Finite Element Method, 有限元) Instead of Springs，考虑力传导

---

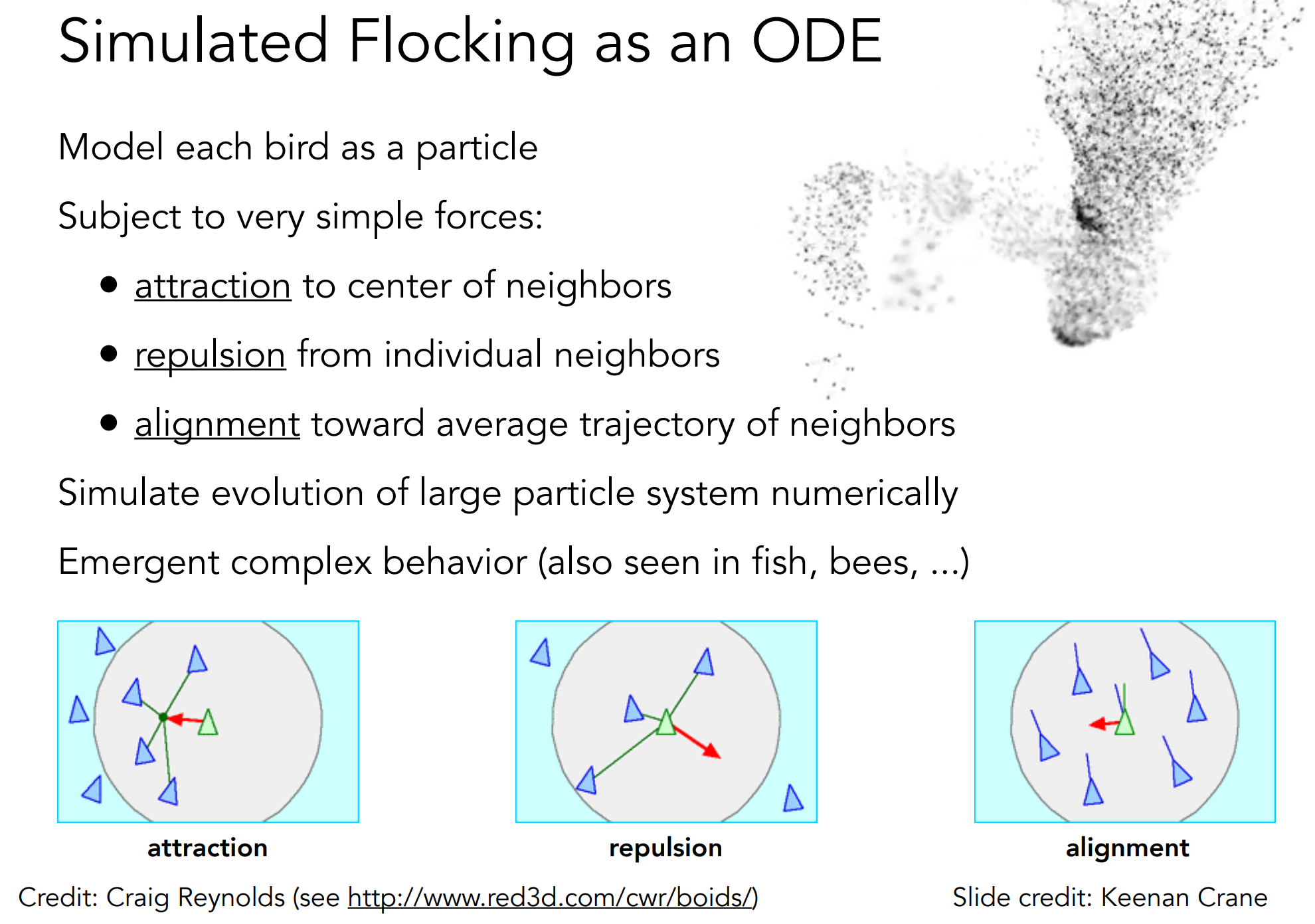
c.2). Particle System

• 粒子系统不仅可描述微小粒子，还可以描述一些群落；
  • 
  • 

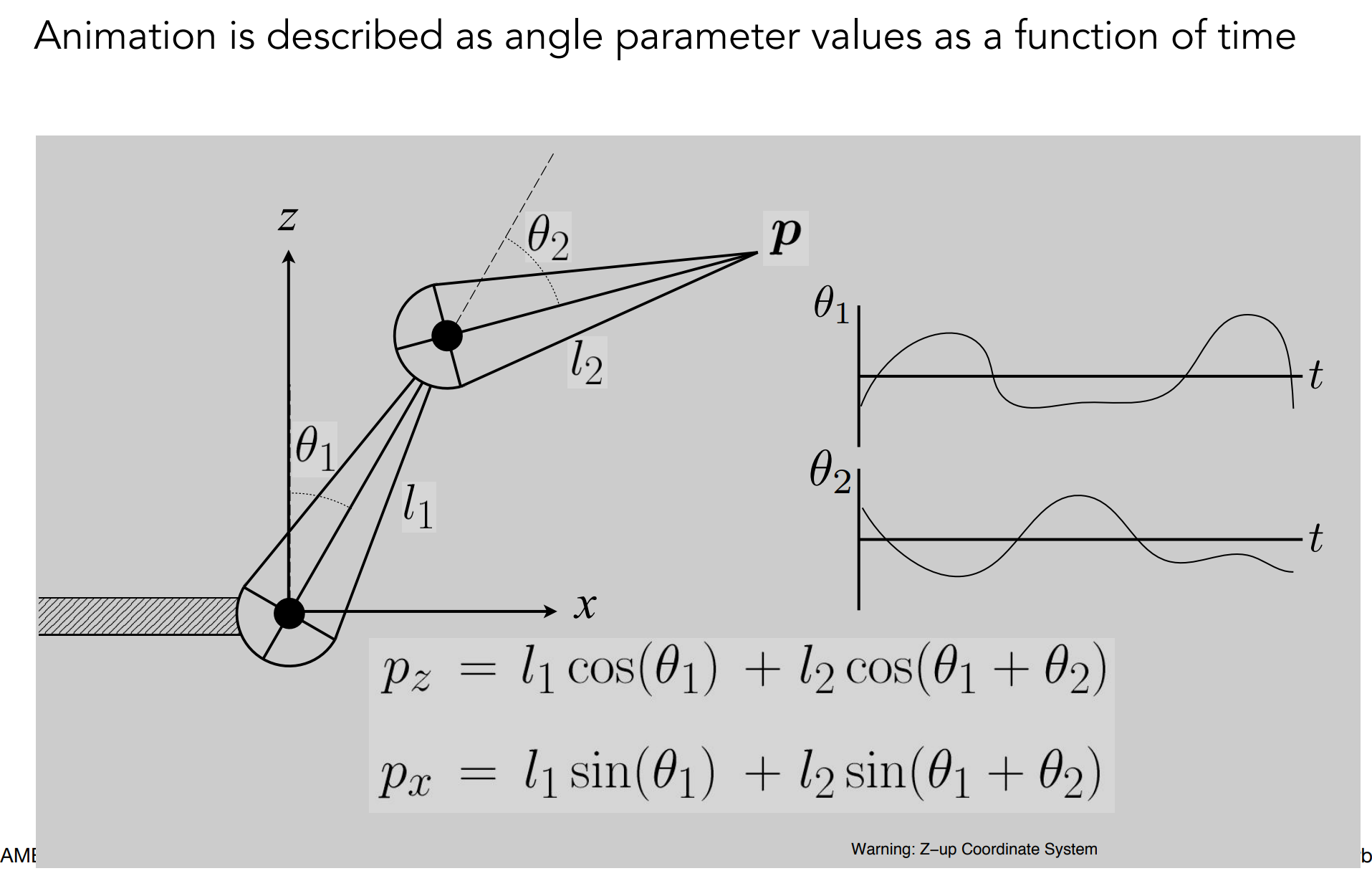
d). Forward Kinematics(FK)

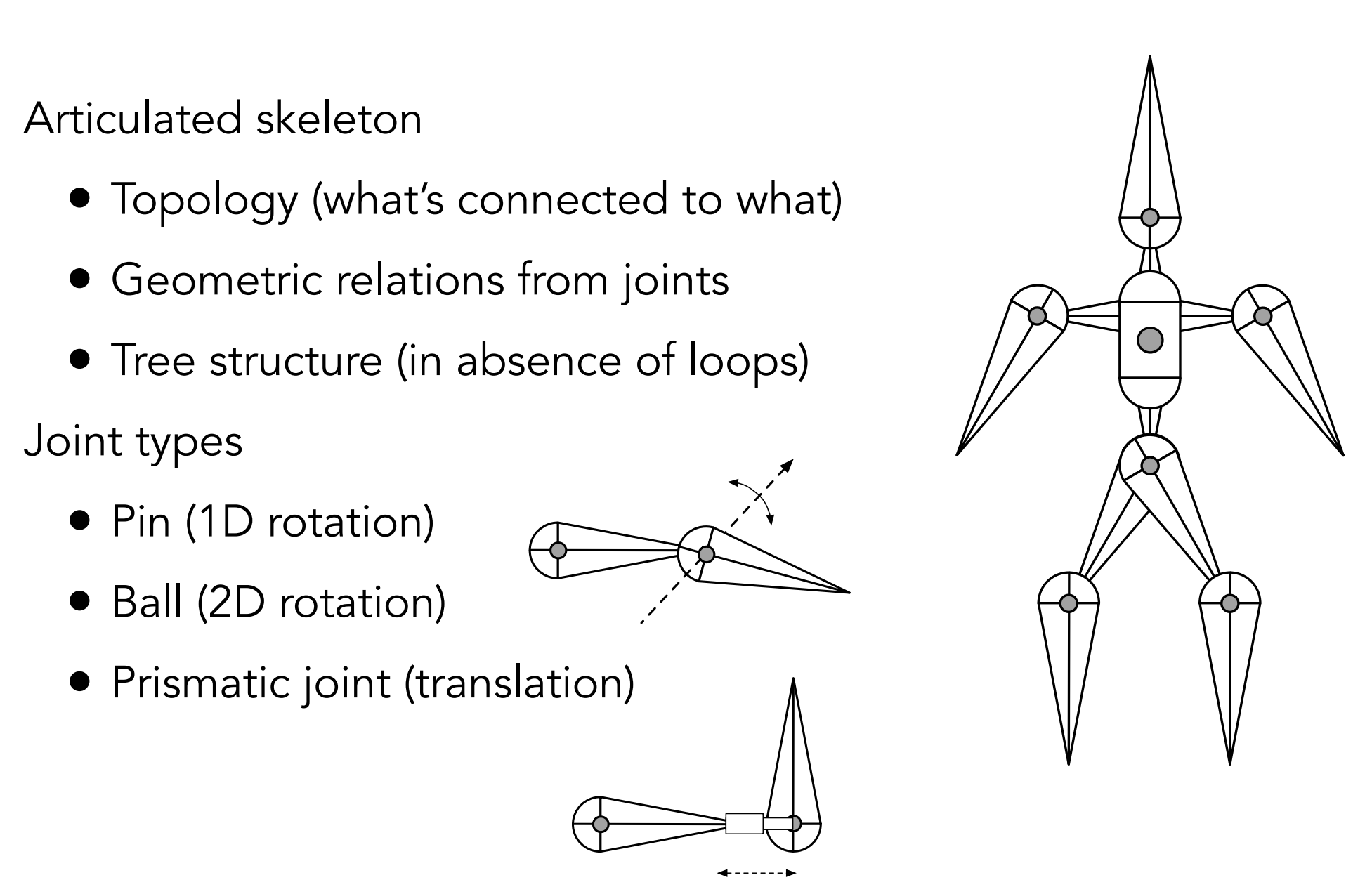
• 关节（Joint）分类：

  

e). Inverse Kinematics(IK)

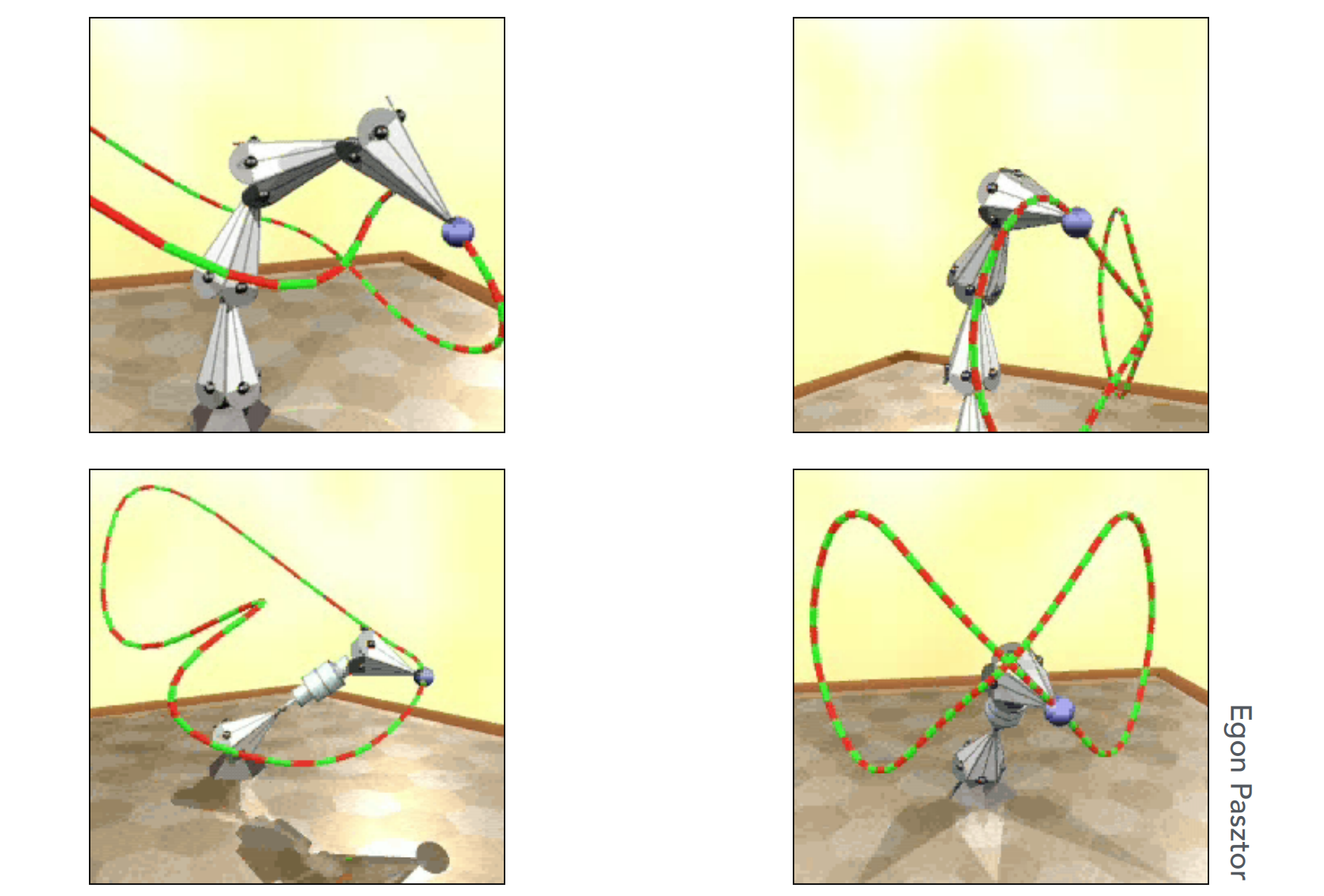
• 解决多个解的方法：梯度下降

f). Rigging

• Blend shapes: 混合控制点或骨骼位置

  

g). Motion Capture / Facial Motion Capture

---

Lecture 22

a). Single Particle Simulation

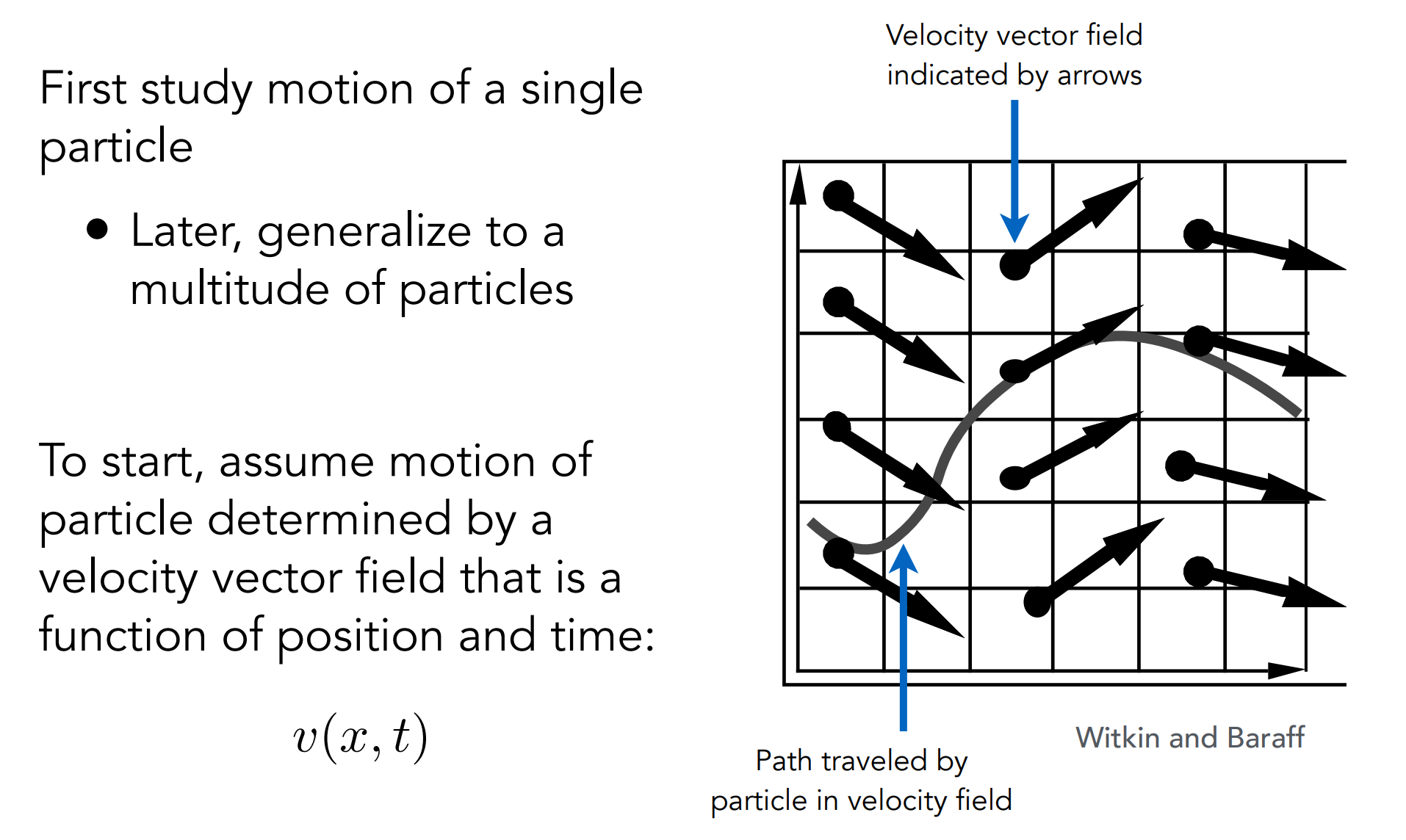
• Velocity vector field: 给定位置，可以得出改点速度。和磁场、电场类似；

• Oridinary Differential Equation(ODE, 常微分方程)

  

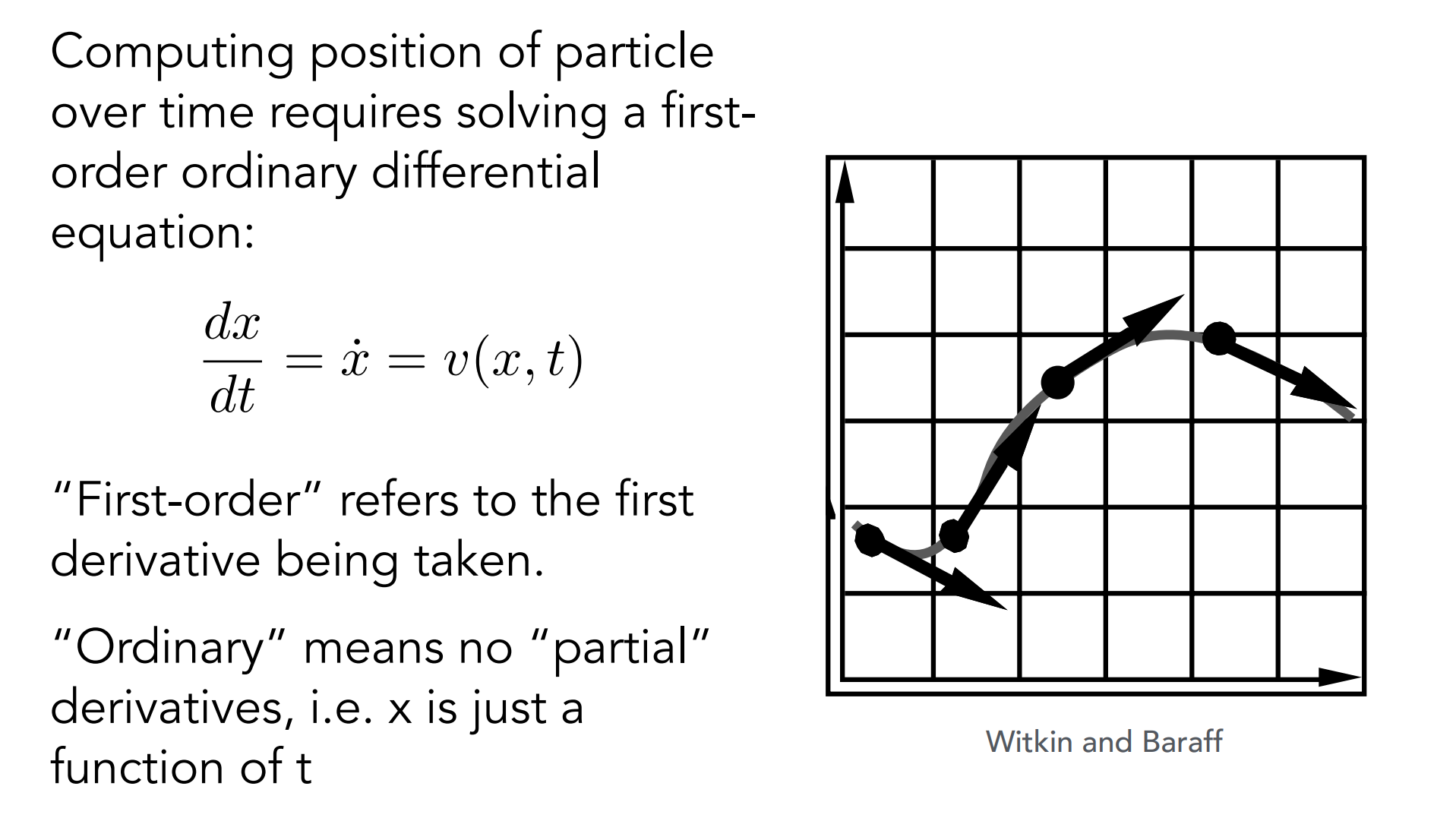
  • 已知解得 t 时刻，粒子的位置和速度，需求得下一时刻的粒子位置；
    • 方法1：显式欧拉法（Explicit Euler method），用差分代替微分，但会引起误差，且稳定性差；

a.1). Euler’s Method

• 缺点：

  1. 存在误差，可通过减小步长（$\Delta t$）来减少误差；

     

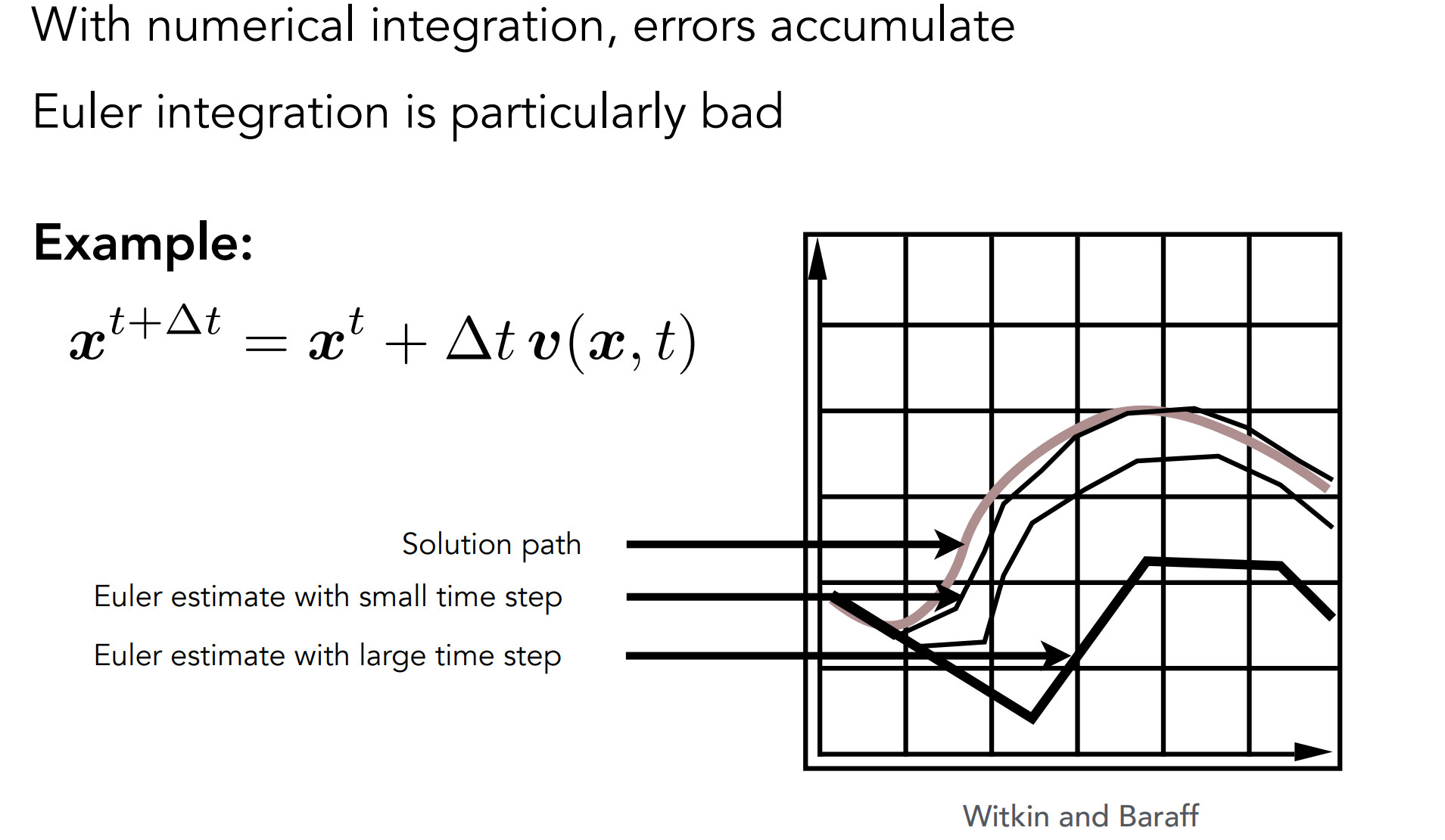
  2. 稳定性差，如速度场为同心圆时，不管步长多小都会逐渐偏移（diverge）

     

a.2). Combating Instability

a.2.1). Midpoint Method

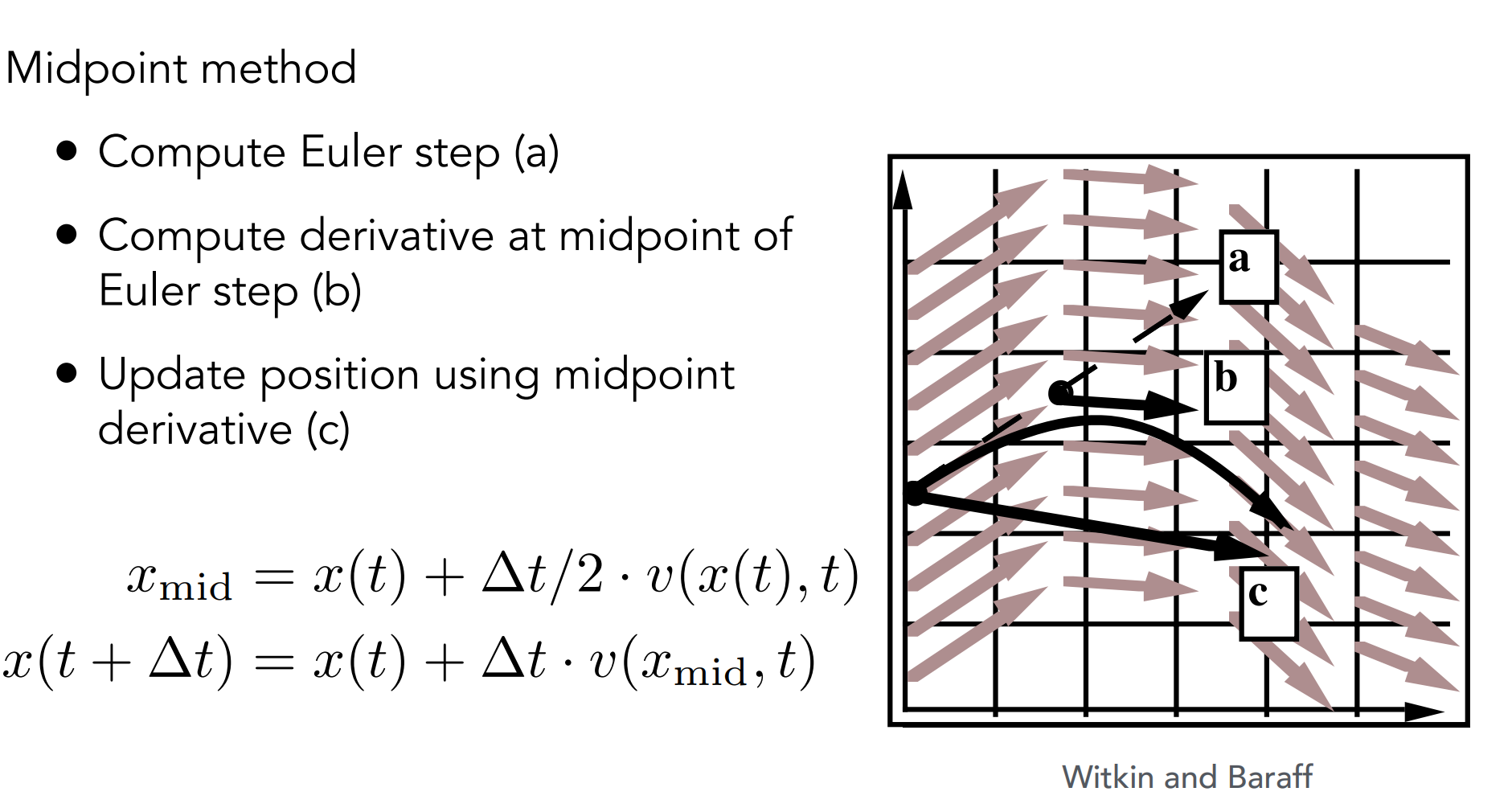
• 计算下一时刻位置后取中点，得到中点速度，在计算下一时刻位置时，使用中点速度

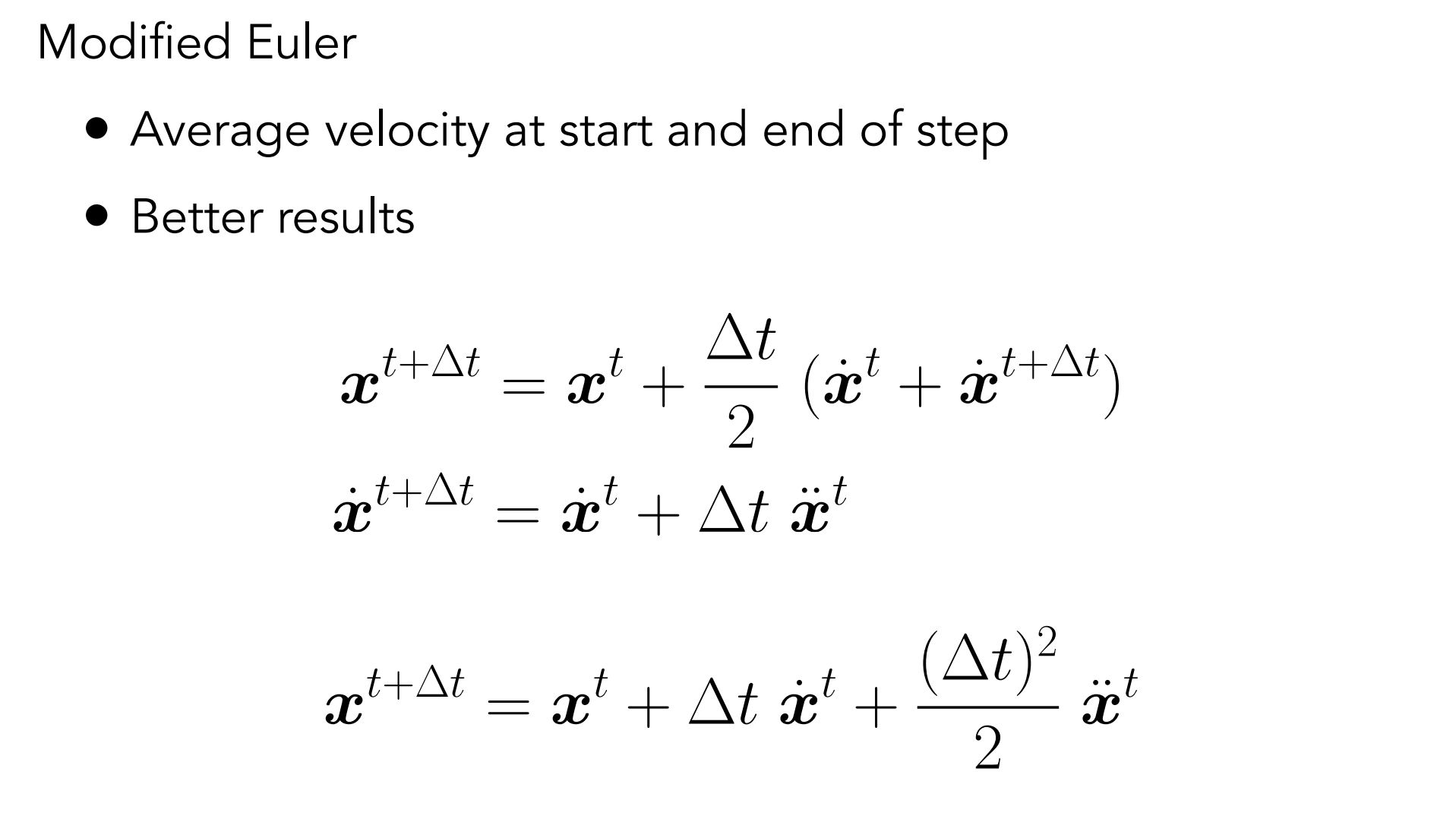
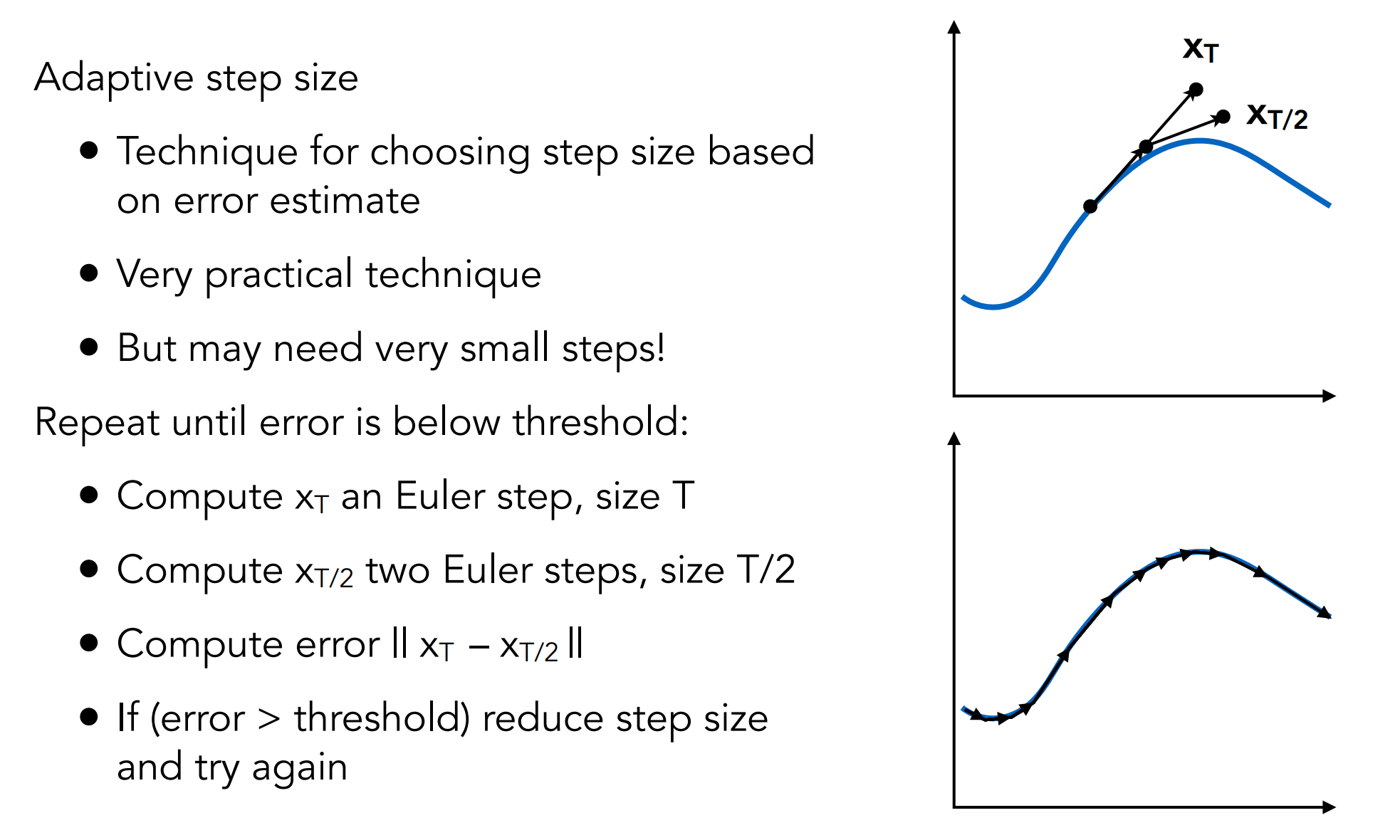
a.2.2). Adaptive Step Size

a.2.3). Implicit Euler Method

• 使用下一时刻的速度和加速度，并求解

、

• 龙格库塔

  

a.2.4). Position-Based / Verlet Integration

• 非基于物理
  • 时间快

---

b). Rigid Body Simulation

• 与单粒子类似

c). Fluid Simulation

c.1). A Simple Position-Based Method

c.2). Eulerian vs. Lagrangian

• 拉格朗日（质点法）：考虑单个粒子的运动

• 欧拉（网格法）：考虑不同位置的网格

• Material Point Method (MPM ，混合上两种方法)