Games202-2 Real-Time Shadow

发表于 更新于 分类于 阅读次数：

a). Shadow Mapping

  • A 2-Pass Algorithm
    1. Light pass: Generate the SM(Shadow Map)
    2. Camera pass: uses the SM
  • An image-space algorithm
    • Pro(优点): no knowledge of scene’s geometry is required
    • Con(缺点): causing self occlusion(自遮挡) and aliasing(走样) issues

Pass 1: Render from Light

  • 输出一张光源视角的深度图（Depth Buffer）

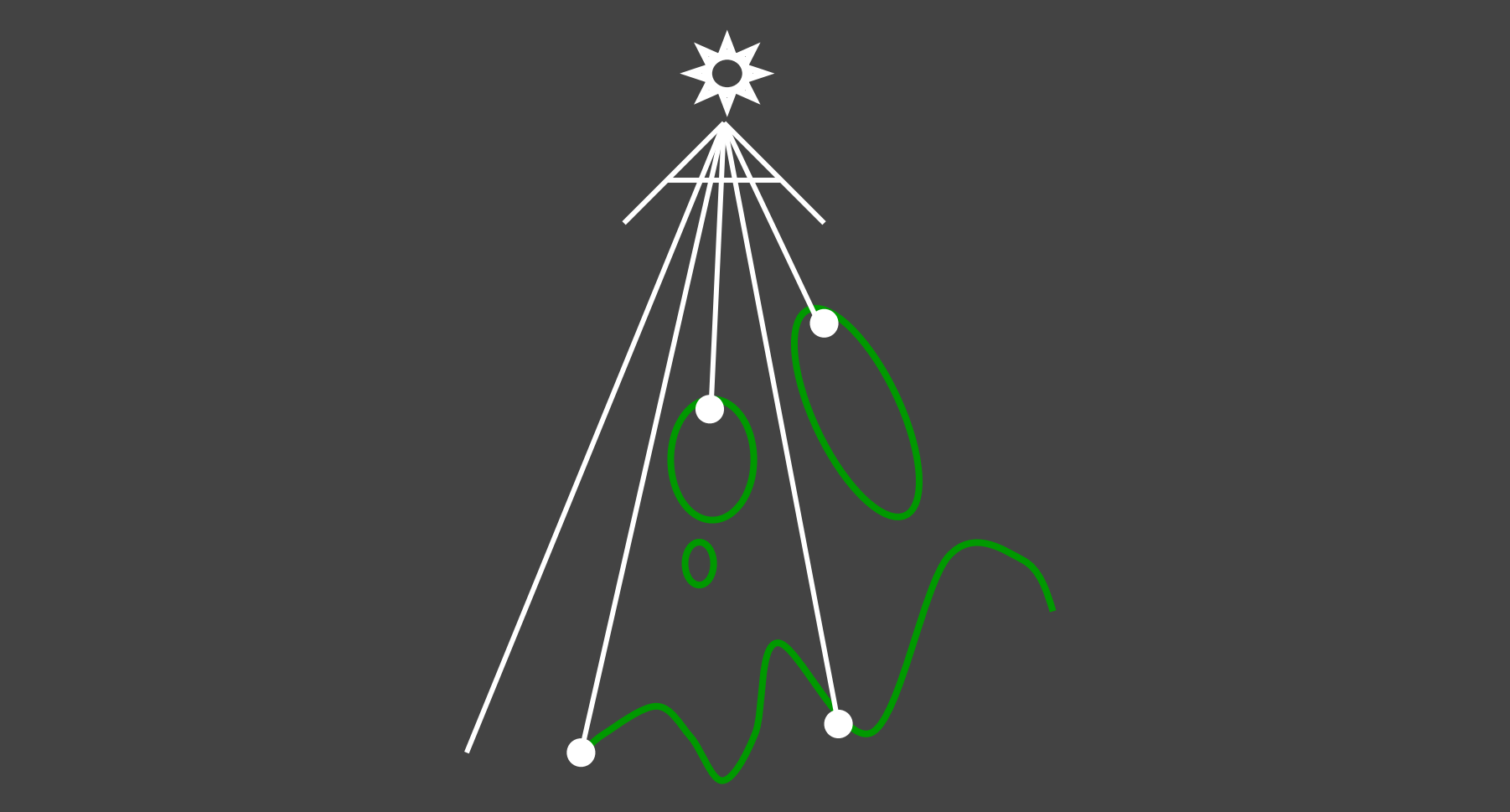
SM_Pass01

Pass 2: Render from Eye(Camera)

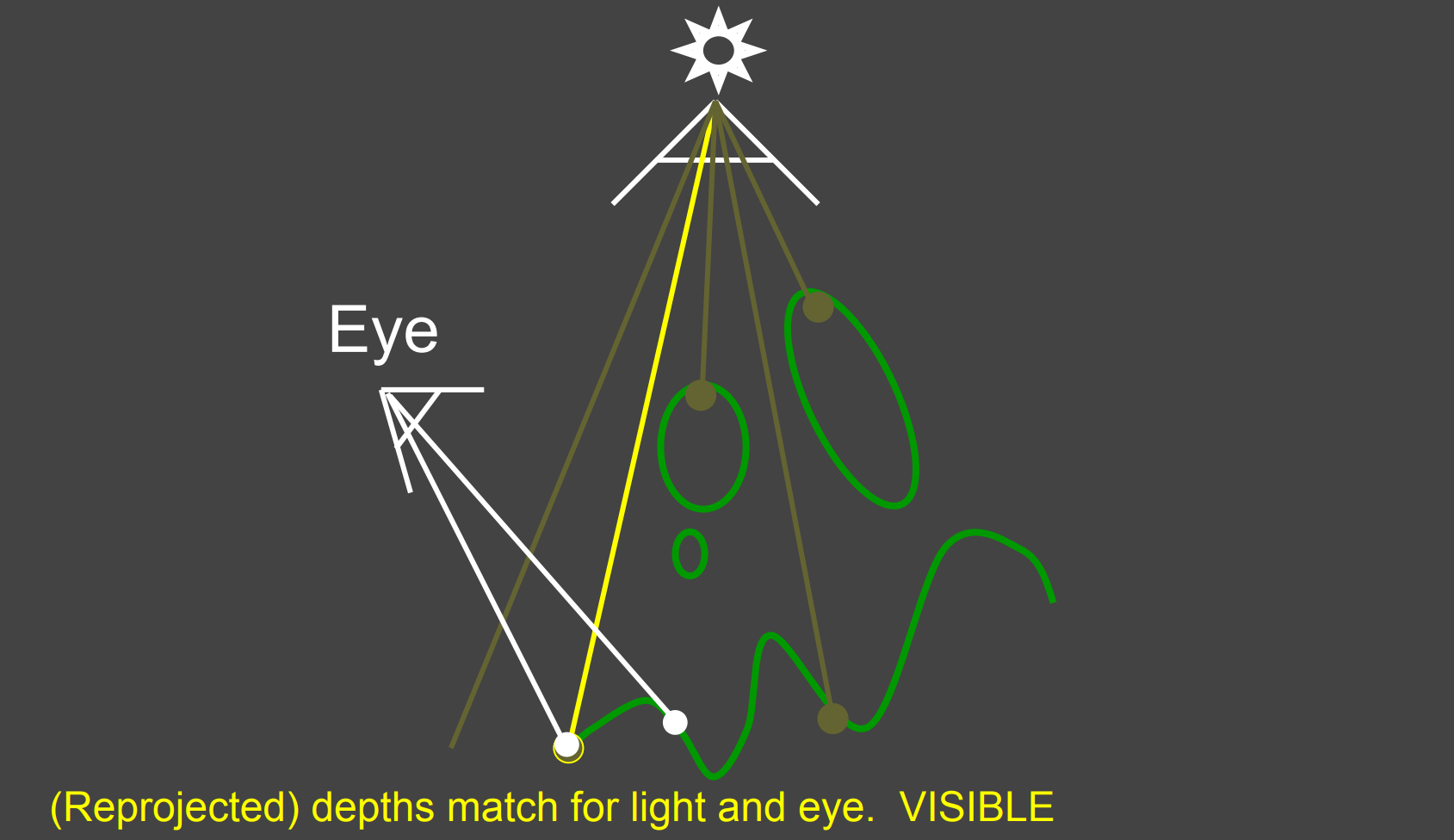
SM_Pass02

  • 将光源视角对应的深度转换到View Space, 与Camera视角的深度进行深度比较；

    • 如$Depth_{cam} > Depth_{light}$ ，那说明该点在阴影中（相机可见，光源不可见）
    • 如$Depth_{cam} < Depth_{light}$ ，那说明该点在不在阴影中（相机可见，光源可见）

  • 用于比较的深度值：

    • 经过透视投影中的Squeez矩阵后（具体看Games101 Math笔记），z会被推向远平面

      $M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
      n & 0 & 0 & 0 \\
      0 & n & 0 & 0 \\
      0 & 0 & n+f & -nf \\
      0 & 0 & 1 & 0
      \end{array}\right)$

    • 用于比较的$Depth$ 可以是经过MVP中的深度值（即Depth Buffer中的深度值）；

    • 也可以是该点在同一空间（如模型空间）中，该点到相机/光源的线性距离；

SM_vs

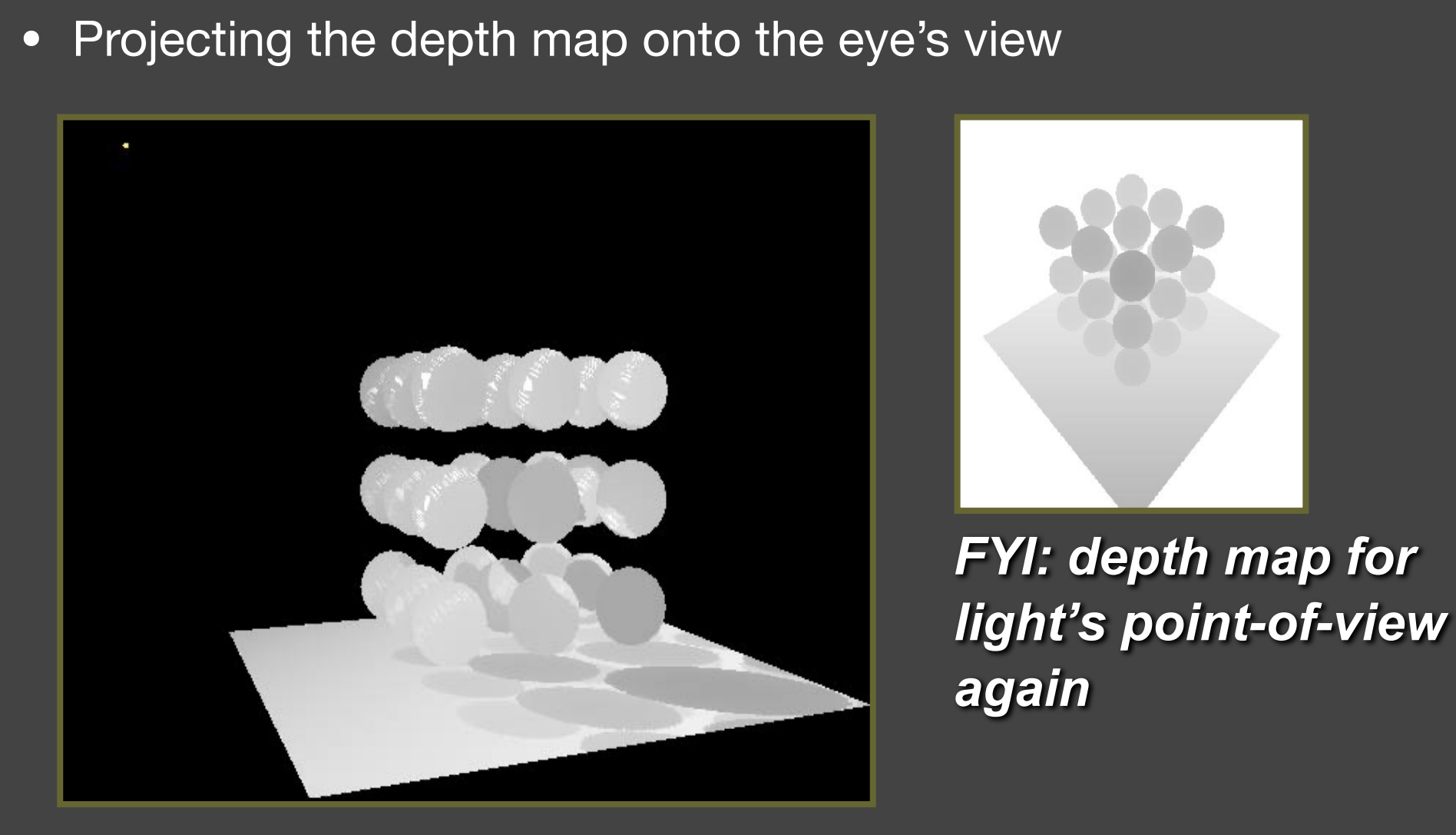
a.1). Issues in Shadow Mapping

a.1.1). Self occlusion(自遮挡)

SelfOcclusion

  • Self occlusion： 阴影自遮挡，造成阴影毛刺的现象；
  • 原因： 如上图，
    • Shadow Map分辨率有限，一个像素内记录的深度值相同。如图中红色和橙色斜线表示Shadow Map中深度相同的位置（$Depth_A = Depth_{A’}$）；
    • 当计算平面中$B$点是否在阴影中时，$Depth_{light} = z1 = Depth_A$，而相机视角下的点$B$转换到光源视角下对应的深度为 $z2$ ，即$Depth_{cam} = z2 = Depth_B$
    • 因此，$Depth_{cam} > Depth_{light}$ ，说明该点在阴影中，因此造成Self occlusion

  • 解决方法： 引入Bias；

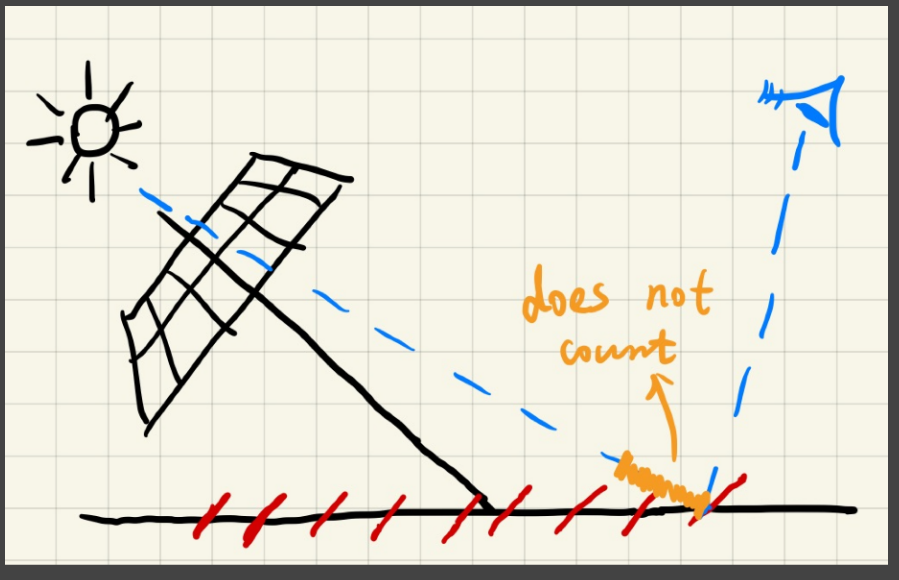
    SelfOcclusion_Bias

    • 认为对于$B$点，如$Depth_{cam} > Depth_{light}$，但$Depth_{light}$ 处于橙色中，那该点仍然不在阴影中；
    • 即：
      • $Depth_{cam} > Depth_{light}+bias$，才使得该点在阴影中；
      • $Depth_{cam} < Depth_{light}+bias$，该点不在阴影中；
    • 易得，当光源方向垂直于平面时，所需的Bias最小，因此可引入光源与平面法线的夹角 $cos\alpha$ ，来调整Bias大小；
  • 引入bias会造成的问题：Detached shadow(不接触阴影，Peter Panning)

a.1.2). Detached shadow

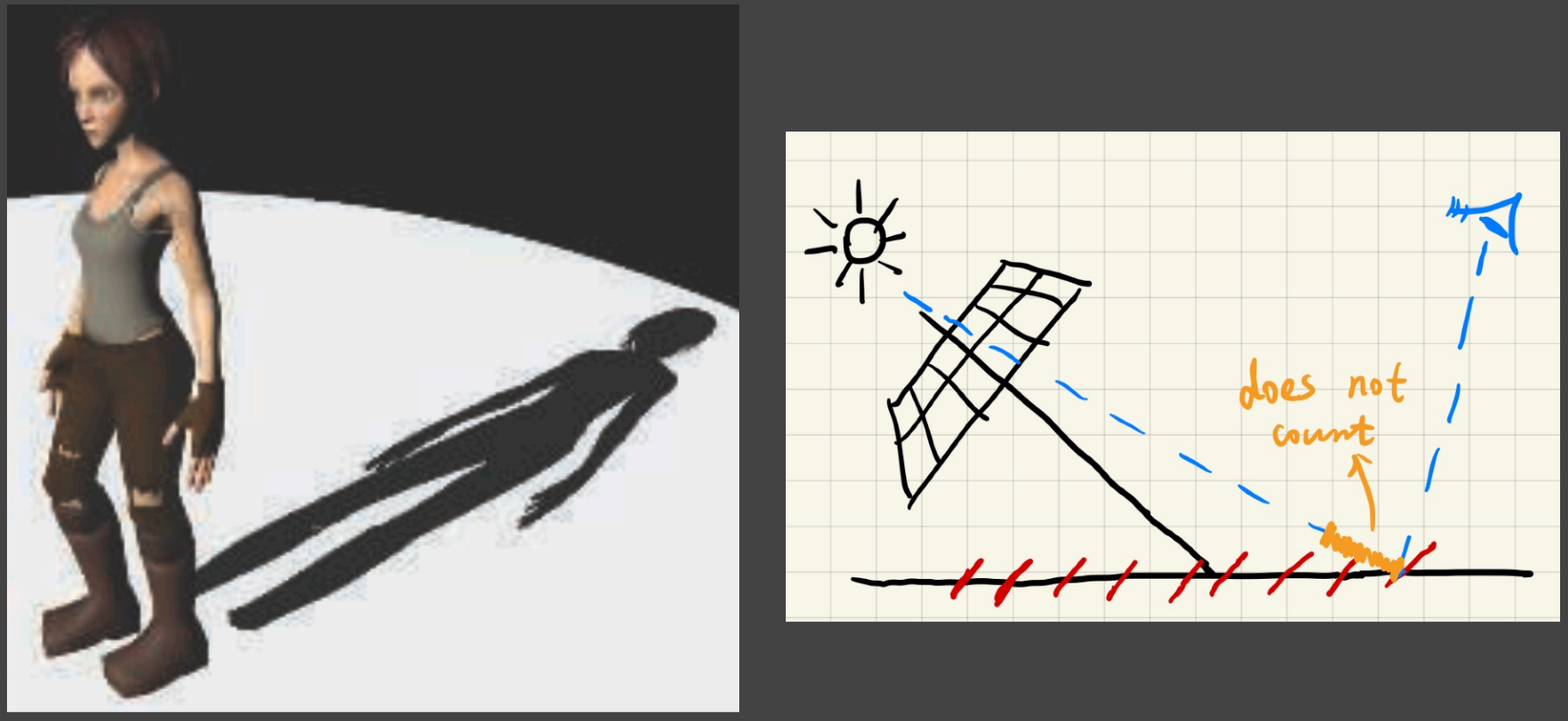
Detached shadow

  • 解决方法：

    • Second-depth shadow mapping

      Second-depthShadowMapping

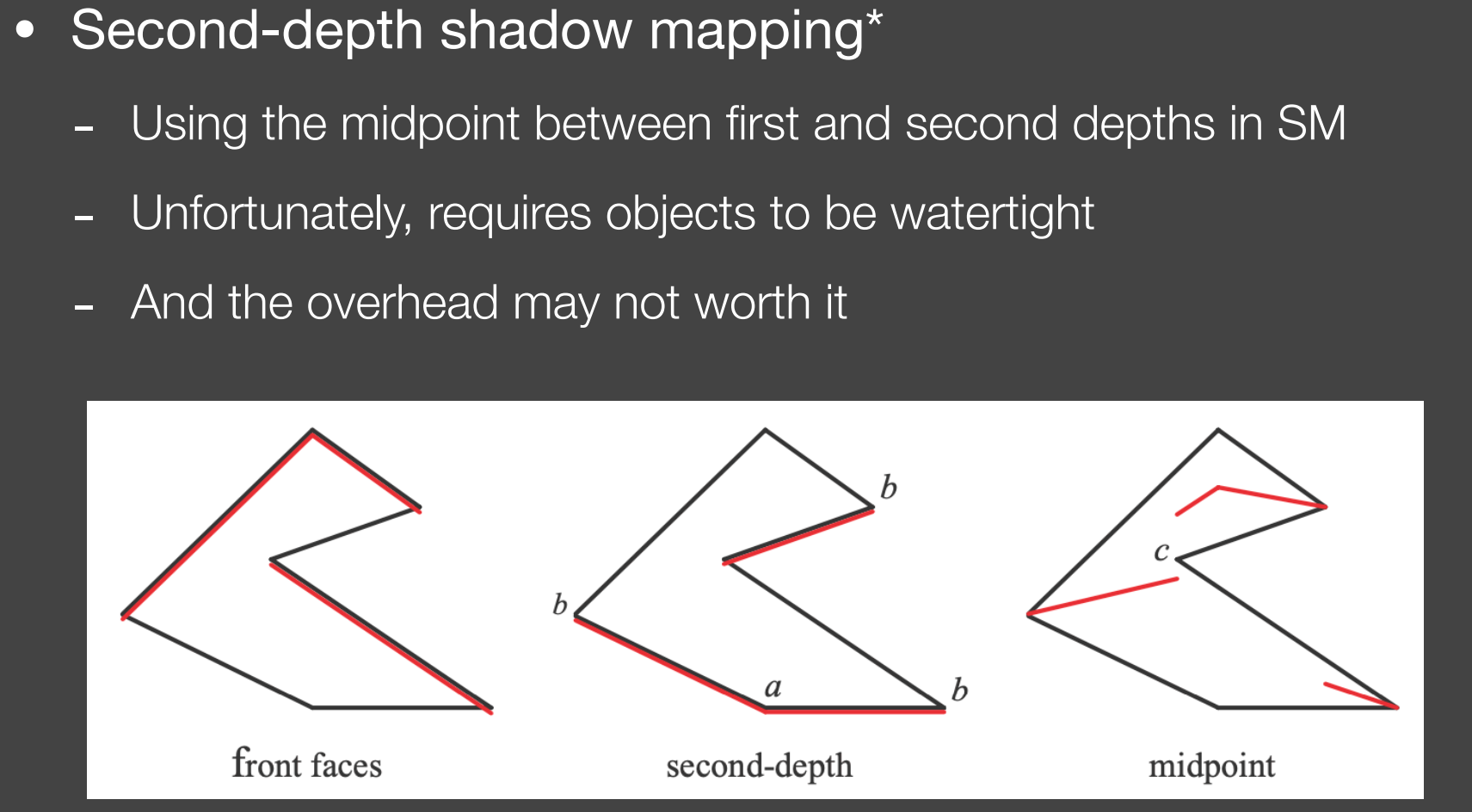
    • 工业界实际没什么人用，只是学术界提出的解决方案

a.1.3). Aliasing

Aliasing

b). Math

b.1). Approximation in RTR

  • RTR中常用的不等式；

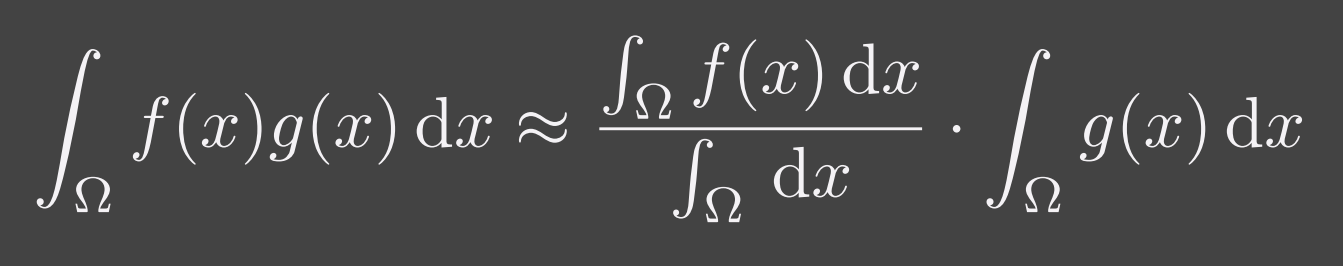
    Approximation in RTR

    • 该不等式“准确”的条件：
      1. Support（支撑集，积分的范围）足够小时；
      2. $g(x)$ 足够光滑（指频率低，起伏小）

b.2). 渲染方程的不等式

ApproximationinRTR_ShadowMap

  • $V(p,\omega_i)$为Visibility，阴影因子；
  • 单独拆出Visibility，即先做shading，后做Visibility，最后相乘

b.3). in Shadow Mapping

什么情况下，Shadow Mapping（先着色，后计算阴影）是准确的；

Small support

ShadowMappingApproximation

  • 在计算阴影中，支撑集小，意味着光源小；
  • 因此，对于点光源和方向光源，做Shadow Mapping硬阴影结果是准确的；

Smooth integrand

对于不等式处理后的渲染方程，$g(x)$ 代表光照。

  • 当$g(x)$ 足够光滑（指频率低，起伏小），不等式为准确的；
  • $L_i$ 光滑，对应光源为面光源；
  • BRDF，即$f_r$ 光滑，对应Diffuse项；
  • 即对于光源为面光源的Diffuse项，不等式处理后的渲染方程是准确的；

c). PCSS(Percentage-Closer Soft Shadow)

PCSS

c.1). PCF(Percentage Closer Filtering)

  • PCF用于抗锯齿，而不用于软阴影（用于软阴影的叫PCSS，两者实质是一个东西，但应用不同叫法不同）
  • 在生成Shadow Map后，阴影比较时（即对阴影比较的结果），进行Filtering
    • 面光源生成Shadow Map：以面光源的中心点(放置相机)生成shadow map

PCF

  • 做法： 不止对着色点与其在Shadow Map中的对应点进行深度比较，而是着色点深度与其在Shadow Map中对应点及其周围点深度进行比较，最后对各个Visibility的结果取平均值（或加权平均）

    • eg1. $P$点在Cam视角下深度为$Depth_p$，转换到光源视角下深度为$Depth_{p’}$，$Depth_{p’}$ 与其在Shadow Map中对应点周围3x3（Filter size）像素进行比较，得到结果取平均得到Visibility为 0.667
  • Filter size
    • Small -> sharper
    • Large -> softer
    • 为选取合适的Filter size，产生了PCSS

c.2). PCSS(Percentage-Closer Soft Shadow)

c.2.1). 什么是PCSS？

  • 关键： 自适应Filter size

PCSS01

  • 观察可得：
    • 钢笔（Blocker）与接收平面（Receiver）的距离越小（笔尖），阴影越硬
    • 钢笔（Blocker）与接收平面（Receiver）的距离越大（笔尖），阴影越软
  • 即阴影的软硬程度，一部分取决于Blocker和Receiver的距离

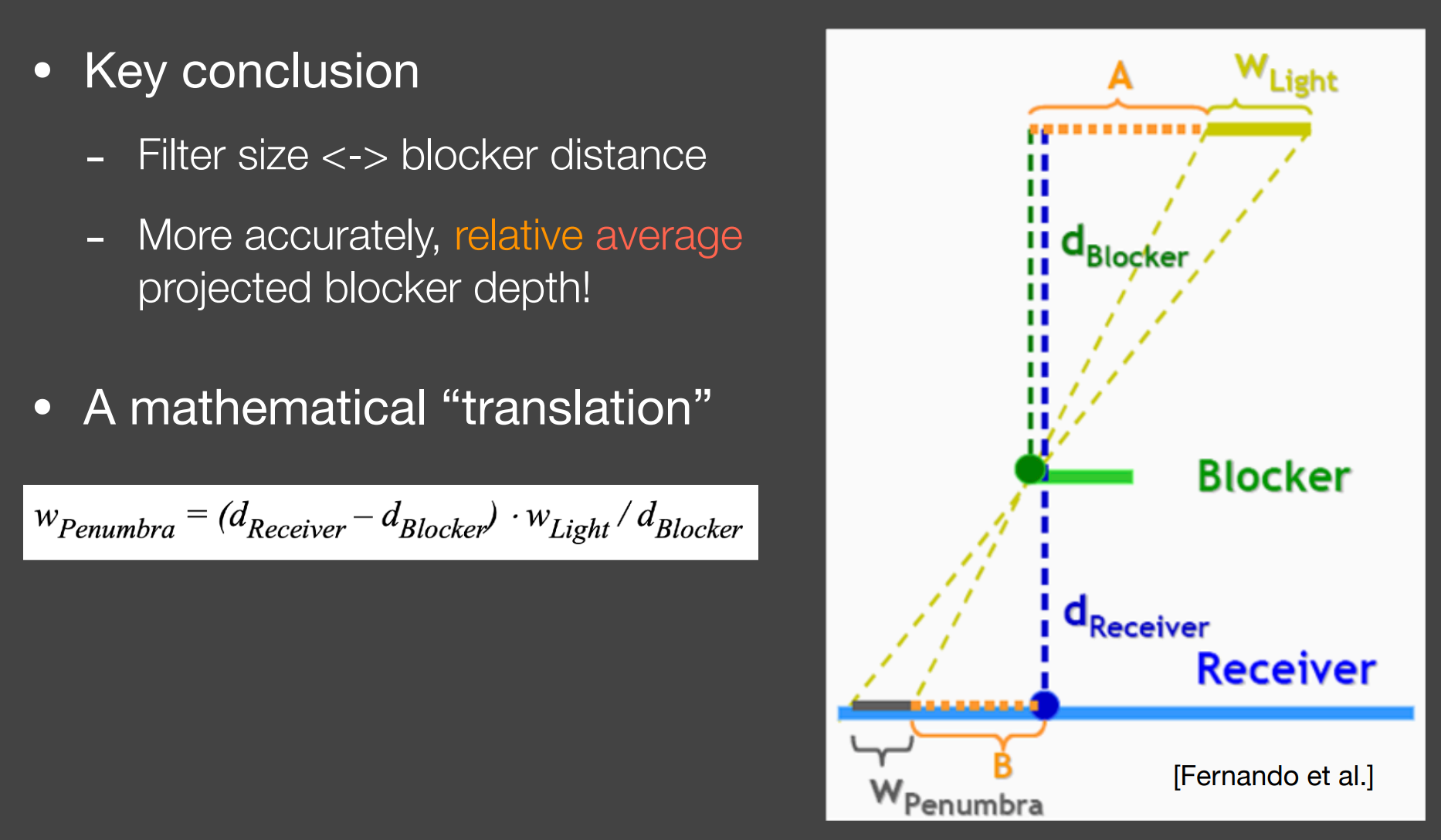
PCSS_Key

  • 阴影的软硬取决于

    • $w_{Light}$ （光源的宽度）
    • $d_{Blocker}$ 与 $d_{BtoR}$ 的比值；

  • Blocker定义：

    Shading point变换到Light视角，对应深度为$Depth_{scene}$ 。查询区域内，深度值$z < Depth_{scene}$ 的texel即为Blocker；

  • $d_{Blocker}$ 为 Average blocker distance

    • Average blocker distance： Shadow Map一定范围内的Blocker的深度平均值

    • 类似eg1

      eg1. $P$点在Cam视角下深度为$Depth_p$，转换到光源视角下深度为$Depth_{p’}$，$Depth_{p’}$ 与其在Shadow Map中对应点周围3x3（Filter size）像素进行比较，得到结果

      取平均得到Visibility为 0.667

      其中，Visibility为0的点，即 处于阴影中，$Depth_{cam} > Depth_{light}+bias$ 的点即为Blocker，对Blocker在Shadow Map中的深度值取平均值，即得到Average blocker distance

c.2.2). 做法

PCSS_How

首先将shading point点$x$投应到shadow map上,找到其对应的像素点$P$。PCSS算法的实现流程如下：

第一步：Blocker search，即获取某个区域的平均遮挡物深度（在点p附近取一个范围(这个范围是自己定义或动态计算的),将范围内各像素的最小深度与x的实际深度比较,从而判断哪些像素是遮挡物，把所有遮挡物的深度记下来取个平均值作为blocker distance。）

第二步：Penumbra estimation，使用平均遮挡物深度计算滤波核尺寸（用取得的遮挡物深度距离来算在PCF中filtering的范围。）

第三步：Percentage Closer Filtering，对应该滤波核尺寸应用PCF算法。

  • 如何动态计算Blocker search的“某个范围”
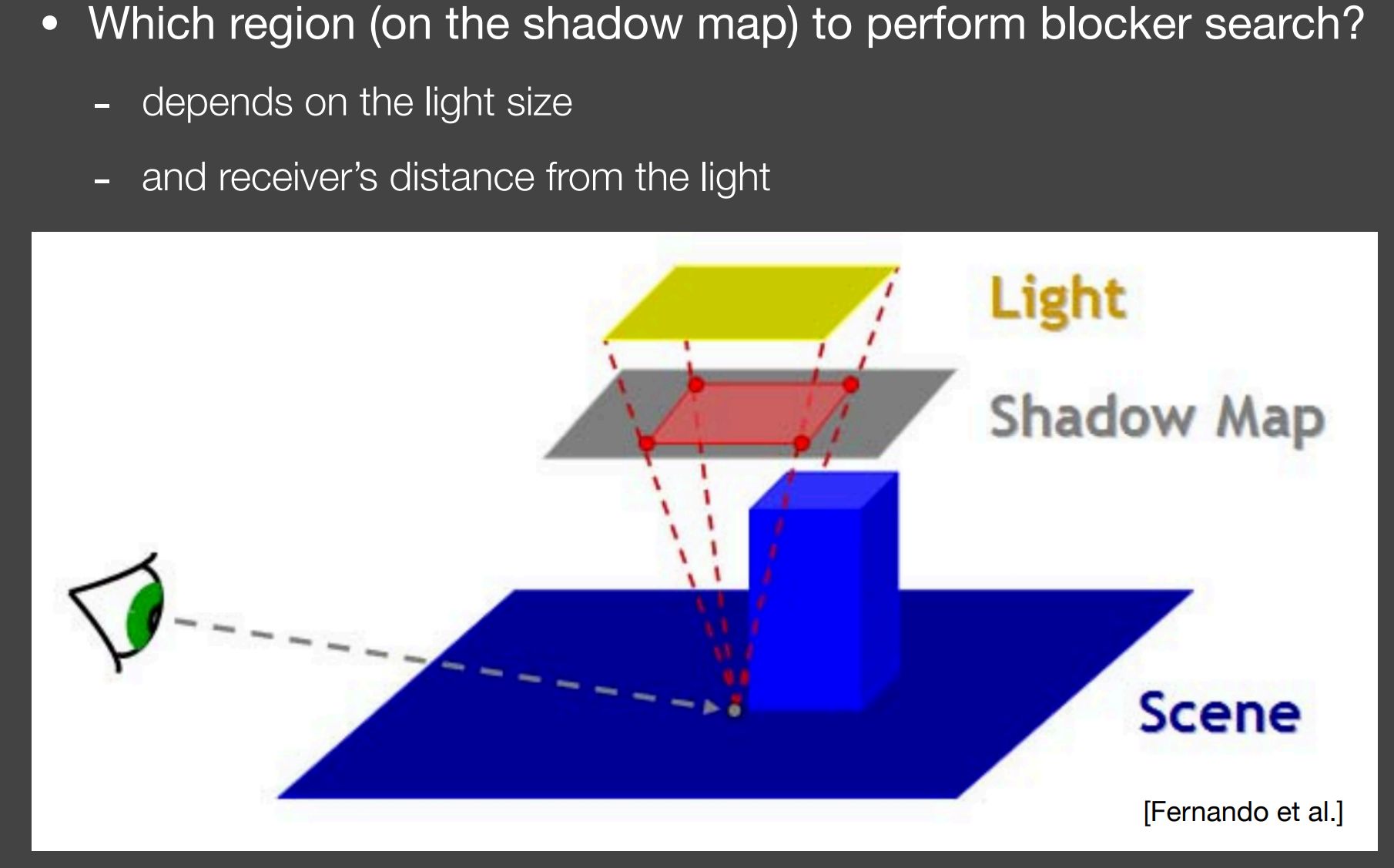
    • PCSS_Region
    • Light越远，Region越小；Light越近，Region越大；（好像和图不太对应，如非要对应，就类似与Shadow Map位置不变，Light距离变大/小）

那么PCSS中那些步骤会导致速度变慢？

  • 第一步：Blocker search，需要多次采样查询深度信息并比较，计算Blocker的平均深度$d_{Blocker}$

  • 第三步：PCF，阴影越软→滤波核尺寸越大→采样查询次数变多→速度变慢

    • 由此可见，主要是多次采样并比较的方法使得速度变慢；

  • 加速方法：

    • 随机采样，后降噪；

    如果觉得区域过大不想对每一个texels都进行比较,就可以通过随机采样其中的texels，而不是全部采样，会得到一个近似的结果,近似的结果就可能会导致出现噪声。工业的处理的方式就是先稀疏采样得到一个有噪声的visibility的图,接着再在图像空间进行降噪。

    • Variance Soft Shadow Mapping(VSSM)

c.2.3). Math

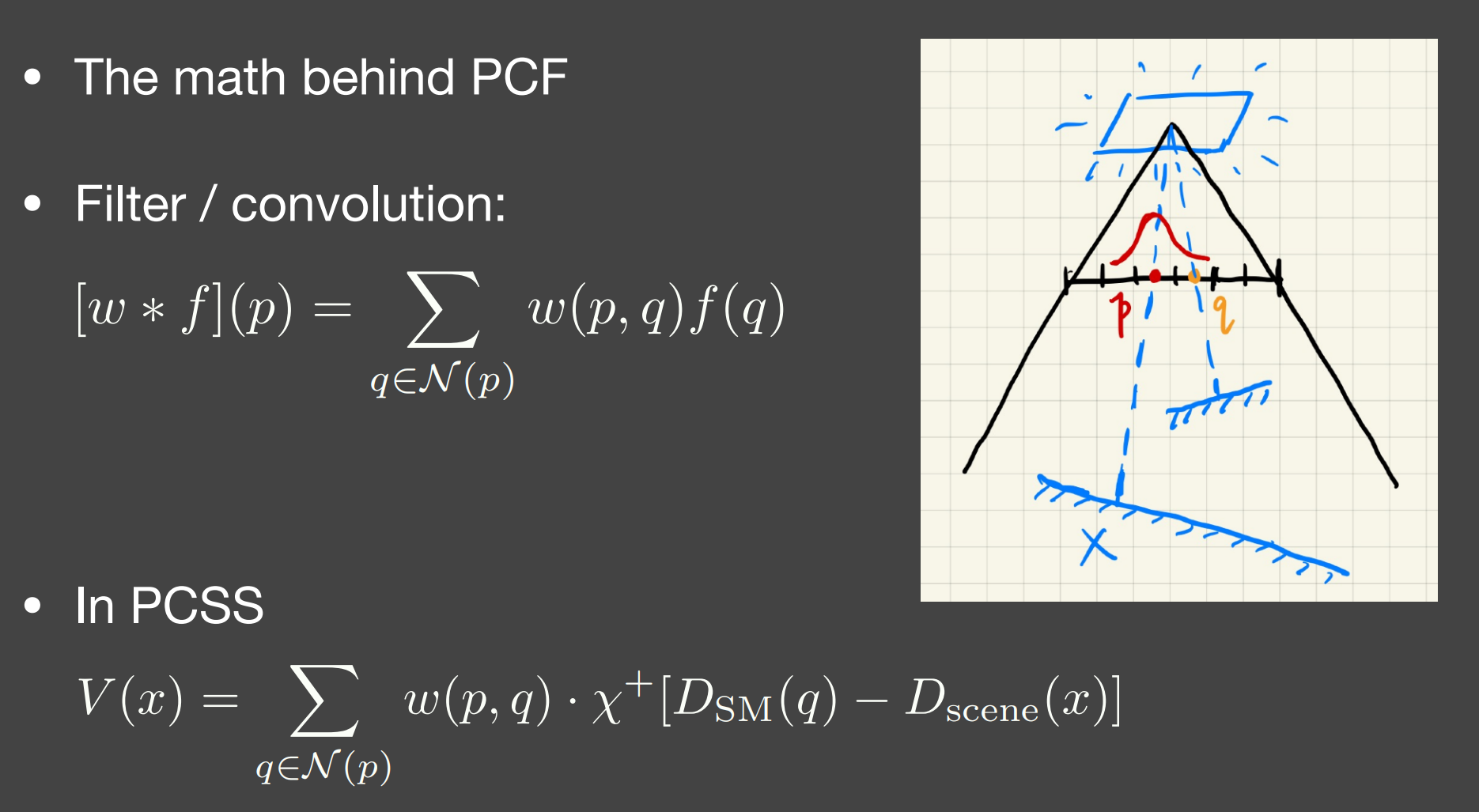
PCF_02

  • 其中$\chi^{+}$ 类似于$step()$ 函数
    • $D_{\mathrm{SM}}(q)-D_{\text {scene }}(x) \geq 0$， 即$Depth_{ShadowMap} \geq Depth_{cam}$，$\chi^{+}\left[D_{\mathrm{SM}}(q)-D_{\text {scene }}(x)\right] = 1$
    • $D_{\mathrm{SM}}(q)-D_{\text {scene }}(x) < 0$， 即$Depth_{ShadowMap} < Depth_{cam}$，$\chi^{+}\left[D_{\mathrm{SM}}(q)-D_{\text {scene }}(x)\right] = 0$

d). Variance Soft Shadow Mapping(VSSM)

  • vs PCSS: Fast blocker search(step 1) and filtering(step 3)
  • 关键思想： 只用知道有多少（百分比）的 texels 在着色点前面；

d.1). Solve step3(PCF)

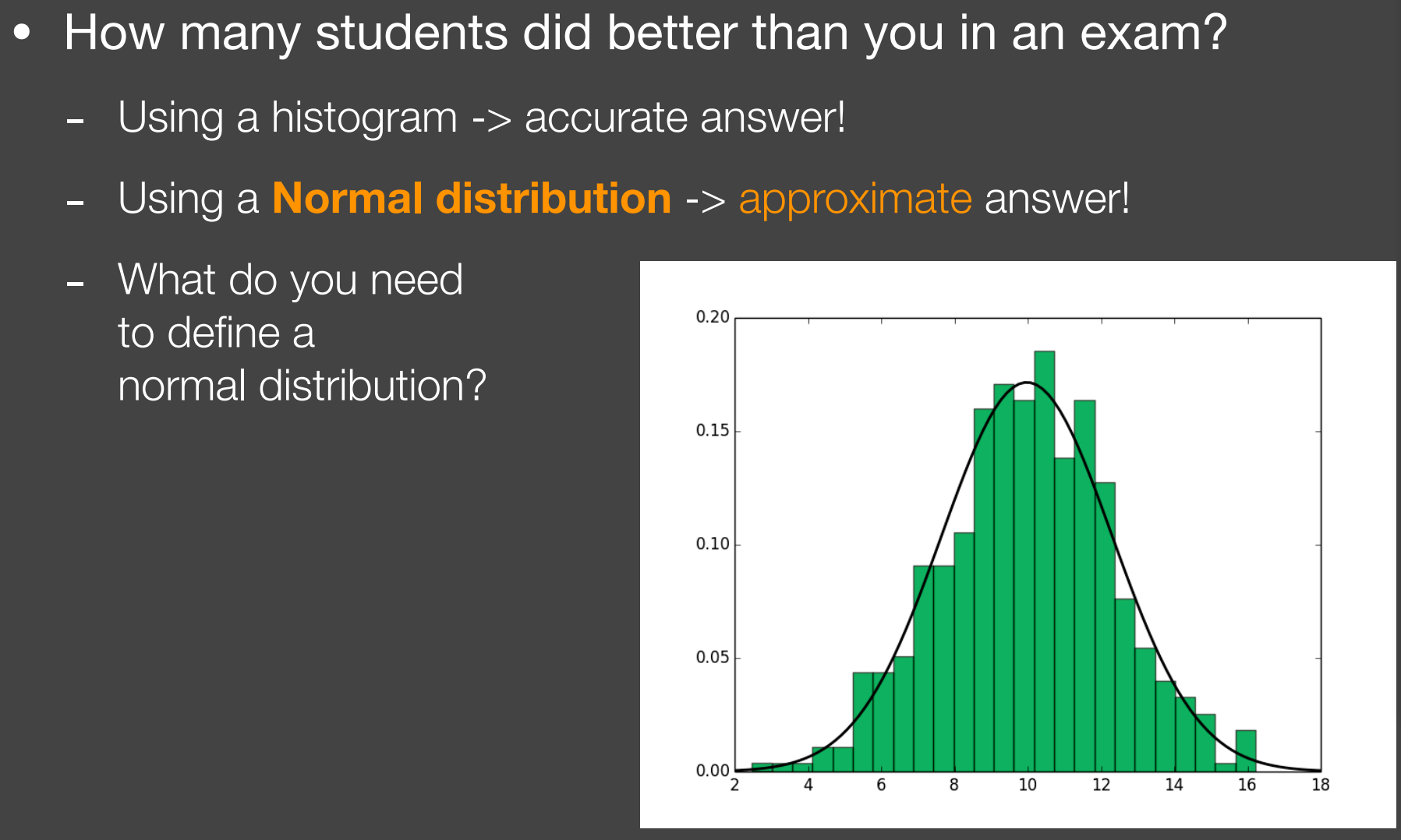
VSSM_01

  • 通过正态分布（Normal distribution），求得着色点的深度在采样点中大概的排位，即可得到近似的结果；

    • 需要定义一个正态分布，需要得知其均值（mean）和方差（variance）

    • Mean:

      1. Hardware MIPMAPing (快，但不一定准确);
      2. Summed Area Tables (SAT, 积分表);
    • Variance:
      • $Var(X) = E(X^2)-E^2(X)$ ，方差等于平方的均值（均方值）减去均值的平方；
      • 只需要在Depth Buffer的空余通道中多存储一个$depth^2$；

  • 通过求正态分布$P(x>Depth_{cam}) (Depth_{cam}为着色点转换到光源视角的深度)$ 的面积，即求CDF（累积分布函数 ）即可求得Visibility

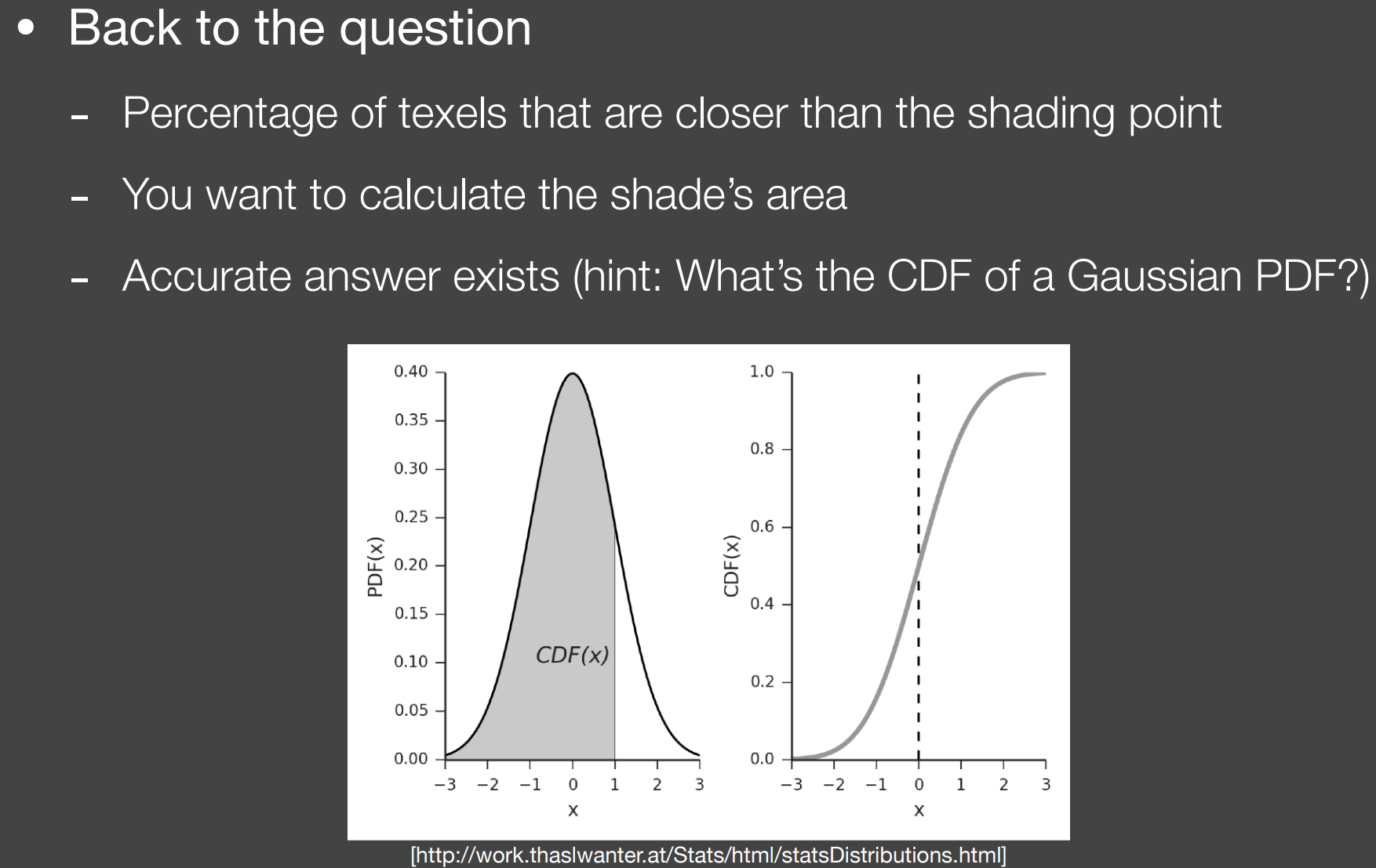
    VSSM_CDF

    • CDF(x) 求解：
      1. 查表；
      2. 切比雪夫不等式；

  • 切比雪夫不等式（并不需要知道具体的分布情况，而是通过不等式直接得出，如使用切比雪夫就不用正态分布，只需要求得均值和方差即可，但是也需要分布情况较为简单）

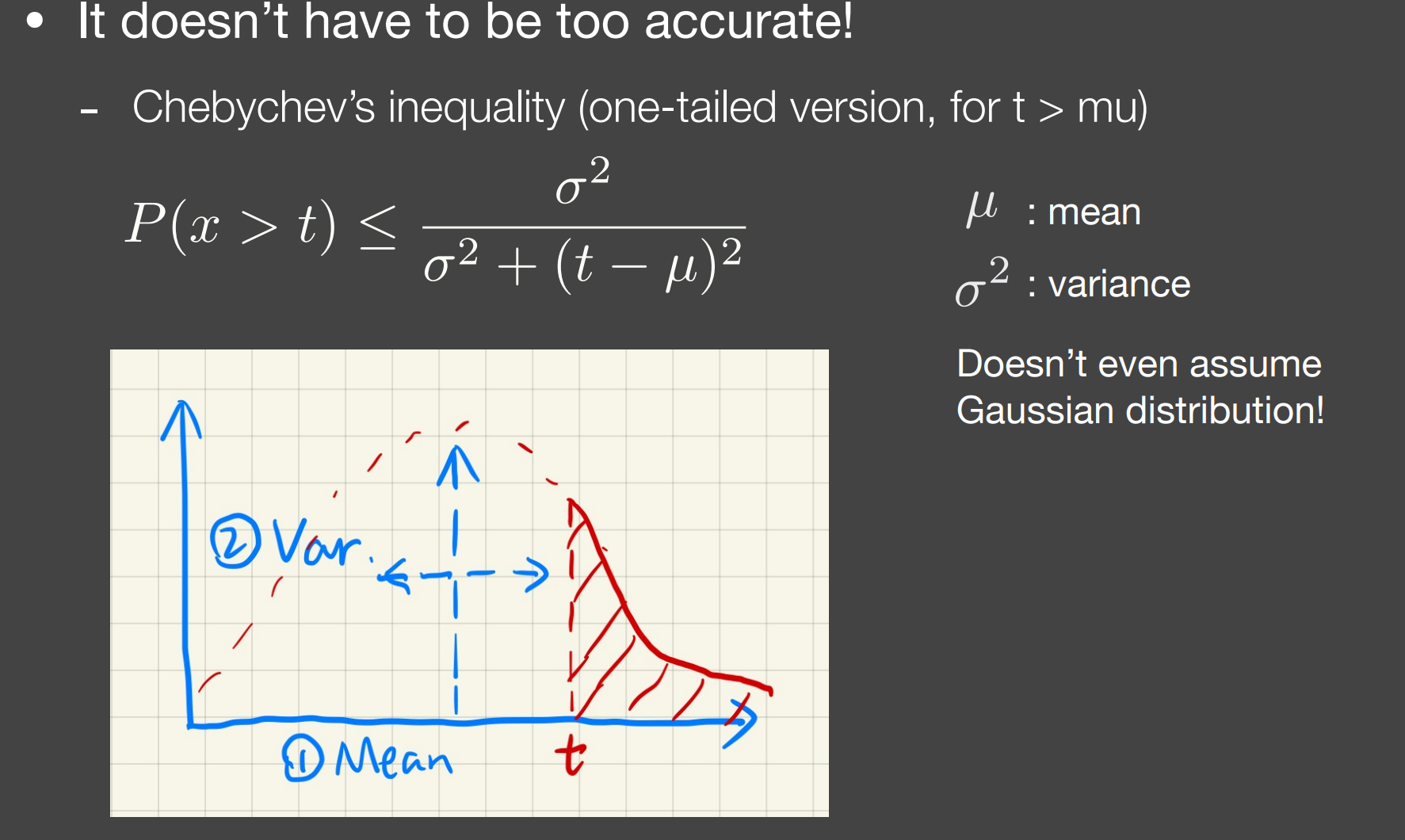
    VSSM_Chebychev

    • 通过近似值约等出Visibility的结果，即红色面积；
      • （准确的条件：）$t\geq mean$ （但一般不管这个，就理解成约等就行）
    • 至此解决了Step3

d.2). Solve step1

VSSM_step01

VSSM_step01b

  • Shading point转换到光源下，

  • 关键式：

    • $\frac{N_{1}}{N} = P(x>t)$ ，通过切比雪夫不等式求出；
    • $\frac{N_{2}}{N} = 1-P(x>t)$
    • $z_{Avg}$：SM中，采样范围深度均值
    • $z_{unocc}$：近似等于$t$
    • 最终，由关键式得出$ z_{o c c}$

d.3). Summed Area Tables (SAT, 积分表)

SAT_1D

  • SAT为数据结构，使用前缀和算法

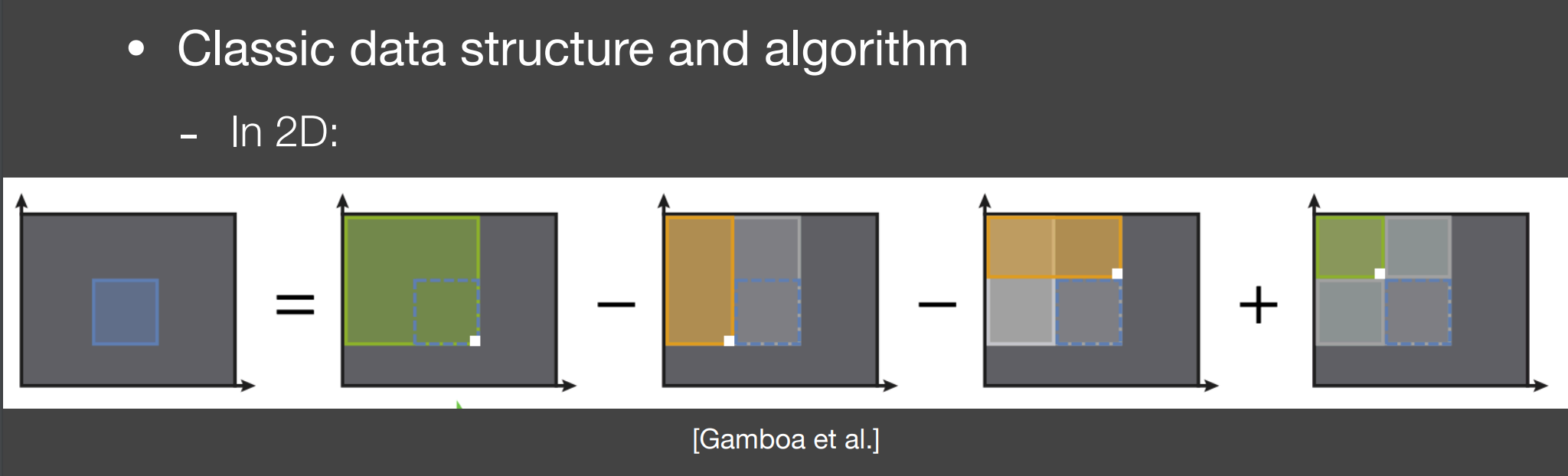
SAT_2D

  • 2D的SAT：每一个点记录左上角区域的和；
    • 先计算一行的一维SAT；
    • 再对计算后的SAT进行列方向的累加，求出二维的SAT；
  • 求蓝色区域和只需要查询四次SAT即可；
  • SAT的并行性：
    • 由于先进行行方向SAT计算，后进行列方向SAT计算，具有一定的并行性；

d.4). 缺陷

由于使用了切比雪夫不等式或正态分布，隐含了Shadow Map中对应范围的深度分布要较为简单或接近正态分布

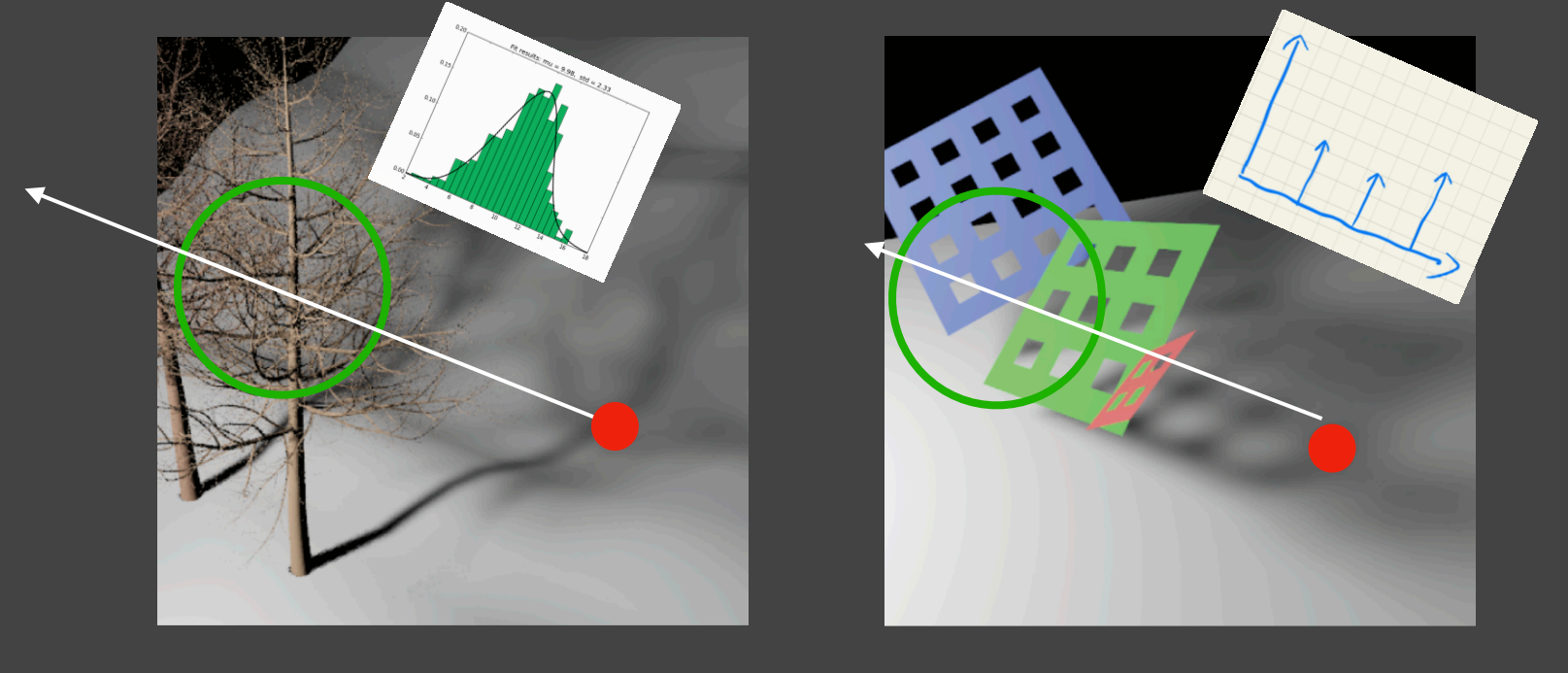
VSSM_Con

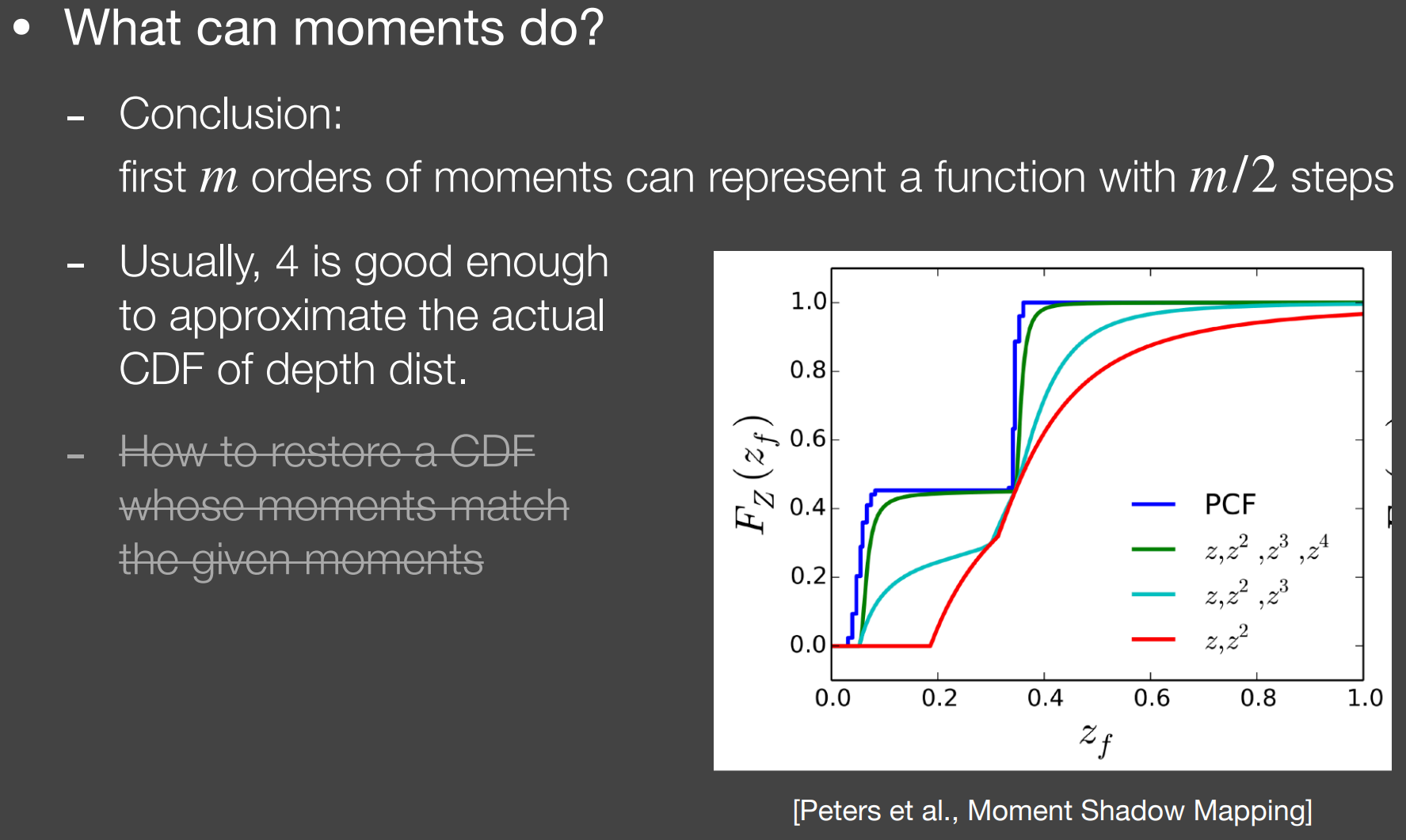
  • 如上右图，分布主要集中在三个值，过于离散，造成VSSM不准确；

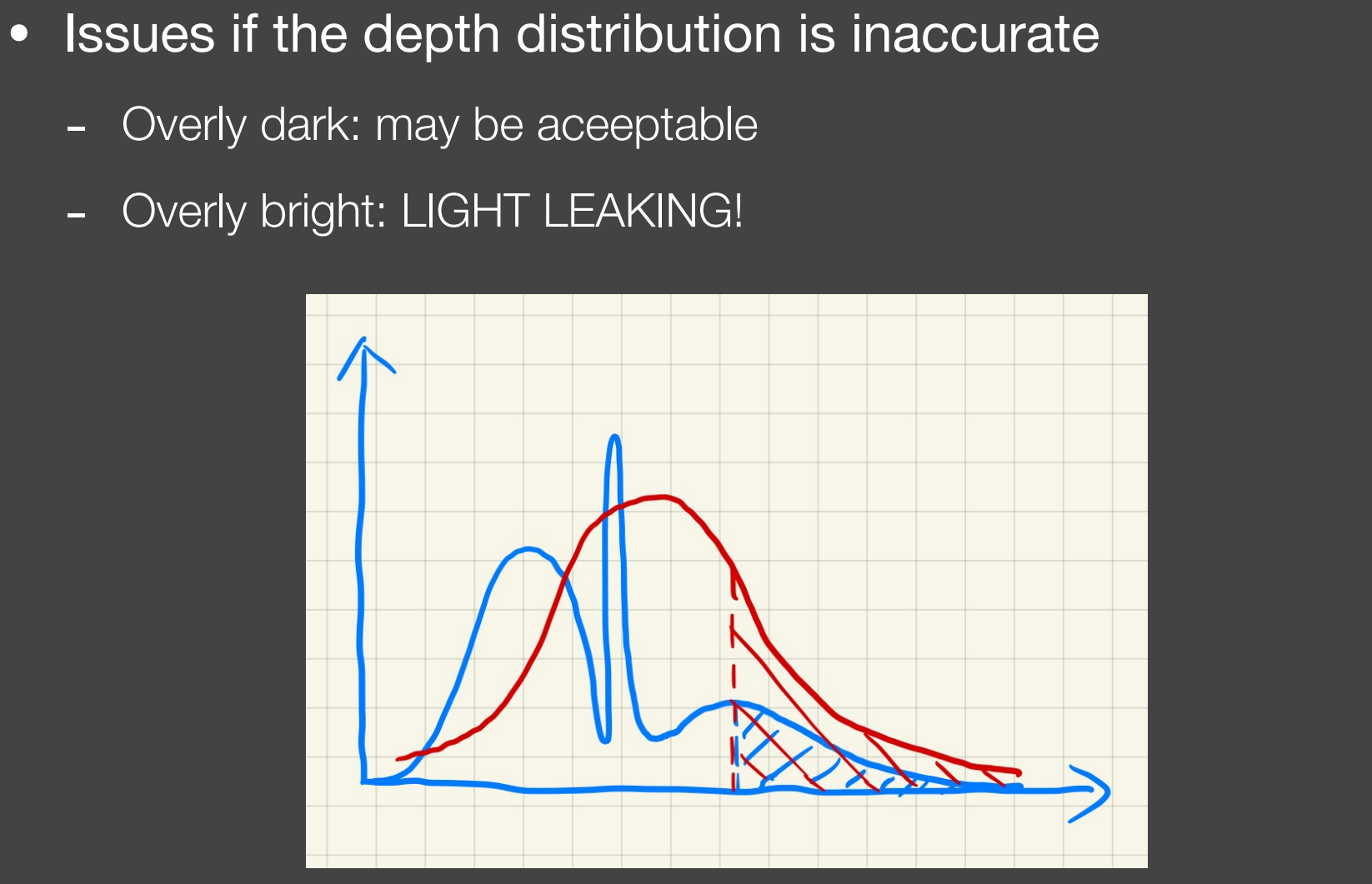
VSSM_Con2

  • Light leaking（漏光）

    VSSM_LightLeaking

e). Moment Shadow Mapping(MSM)

  • VSSM不够准确，需要用更高的矩（Moment）来描述PCF（Use higher order moments to represent a distribution）

  • 矩（Moments）：

    • Quite a few variations on the definition

    • We use the simplest:

      $x,x^2,x^3,x^4,…$

    • VSSM中，我们用到了二阶矩（$depth^2$）

    • 有点类似于展开（比如泰勒展开）；

MSM_Moments

MSM_ProAndCons

f). Distance Field Soft Shadow(SDF, 有向距离场)

f.1). Distance functions

  • 定义： 对于空间中任意一点，其值为到物体的最近距离。并且可定义其在内部符号（Signed）为负，在外符号为正，即为有向距离场（Signed Distance Functions, SDF）;

    DF

  • An Example: Blending (linear interp.) a moving boundary

    SDF_01

    SDF_02

  • 背后理论： 最优传输（Optimal Transport）

  • SDF性质：

    • 对于刚体，SDF不需要实时计算；
      • $n$个刚体运动，对于一个点$P$ ，就有$SDF_1(P), SDF_2(P)……SDF_n(P)$，那该点最后的SDF值即为$min(SDF_1(P), SDF_2(P)……SDF_n(P))$
    • 对于形变的物体，SDF需要实时计算；

  • 用途：

    • Ray marching
    • 软阴影

DistanceField

  • WARNING：不要看到图形就认为SDF是存储一张图形，SDF是三维存储，对于空间中每一个点都有其SDF值

f.1.1). Ray marching

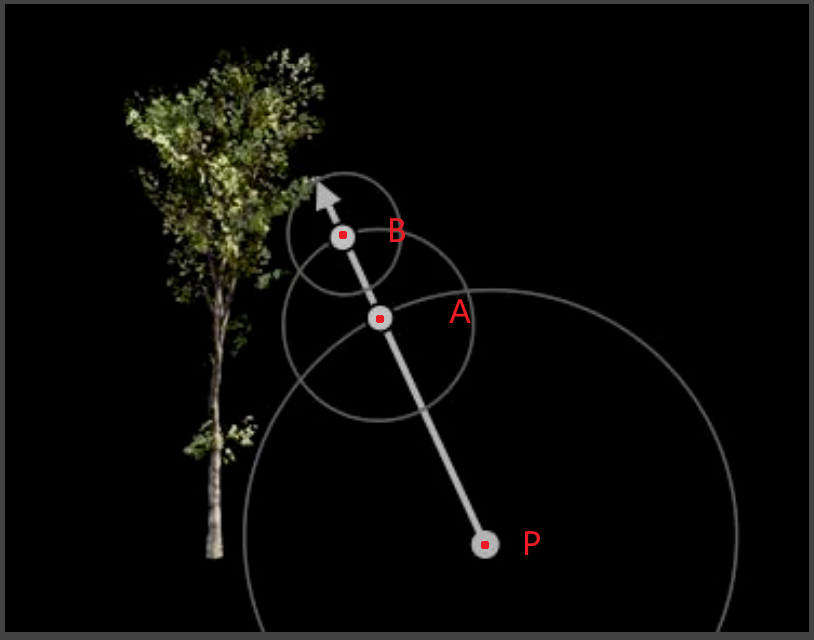
RayMarching

  • 作用：Ray marching(sphere tracing)用来在SDF中射线与物体求交

  • 关键思想：

    SDF中一点的值，即是该点与周围物体不相交的“安全距离”。如对于点$P$，在周围半径为$SDF(P)$ 的距离内，不与物体相交；

    • 因此，以图为例，求SDF中射线与物体相交只需要依次步进$SDF(P)$ , $SDF(A)$ , $SDF(P)$，只需要终点的$SDF(Last)$ 小于一定值，即该点为交点（或一定次数步进后仍没交点，说明该点无交点）

f.1.2). Soft Shadow

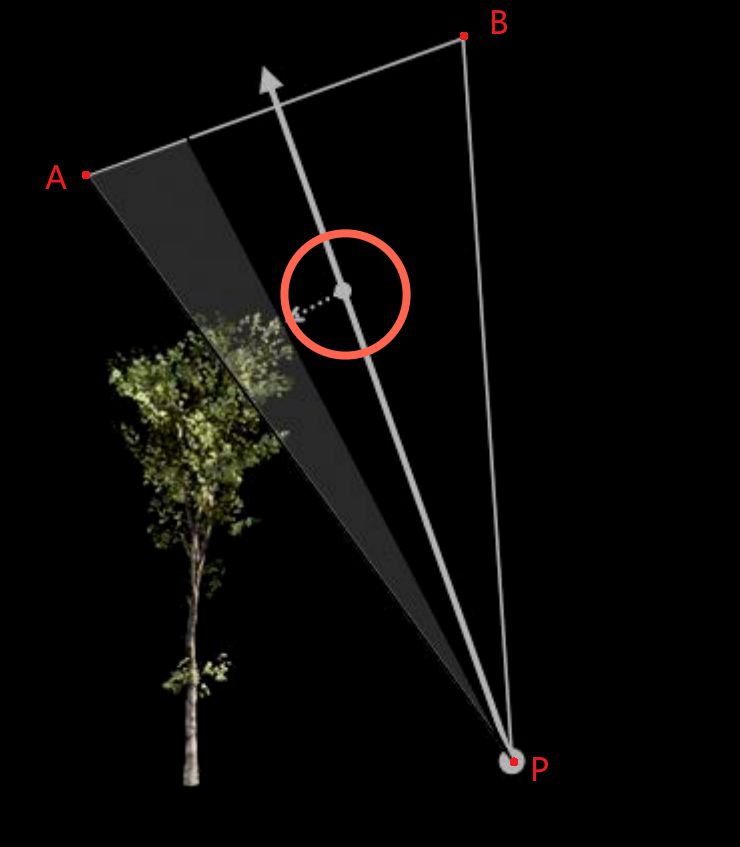
SDF_SS

  • 作用： 使用SDF来近似表现遮挡百分比（Visibility）

  • 关键思想：

    SDF中一点的值，即是该点实现不被某一物体遮挡“安全角度”

    • 如着色点$P$看向面光源$AB$，通过得到射向面光源中点的Ray marching来得到”安全角度”。通过安全角度在总角度中的占比，来近似Visibility
    • Smaller “safe” angle <-> less visibility

  • 安全角度：

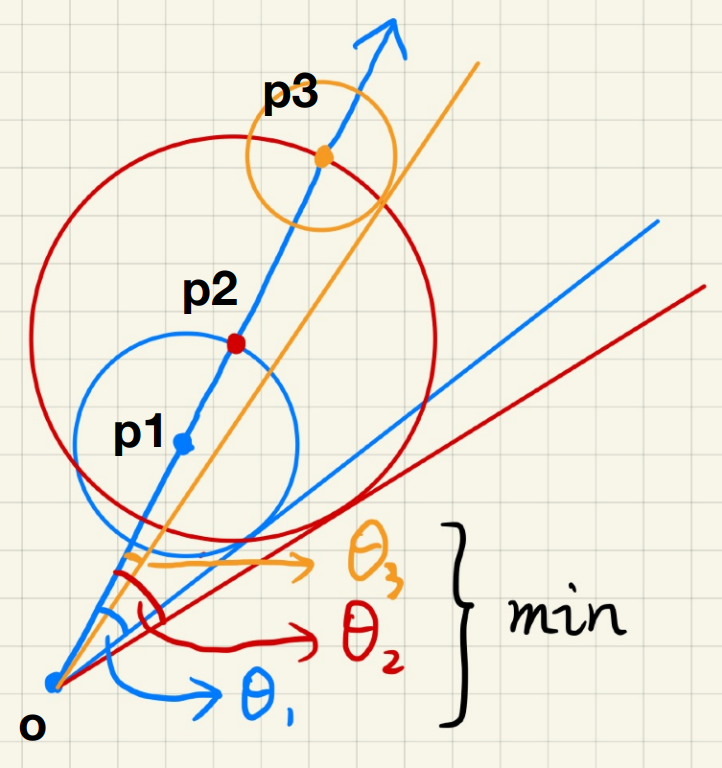
    SDF_SS02

    • 缺点： 在shader中涉及反三角函数，开销大；

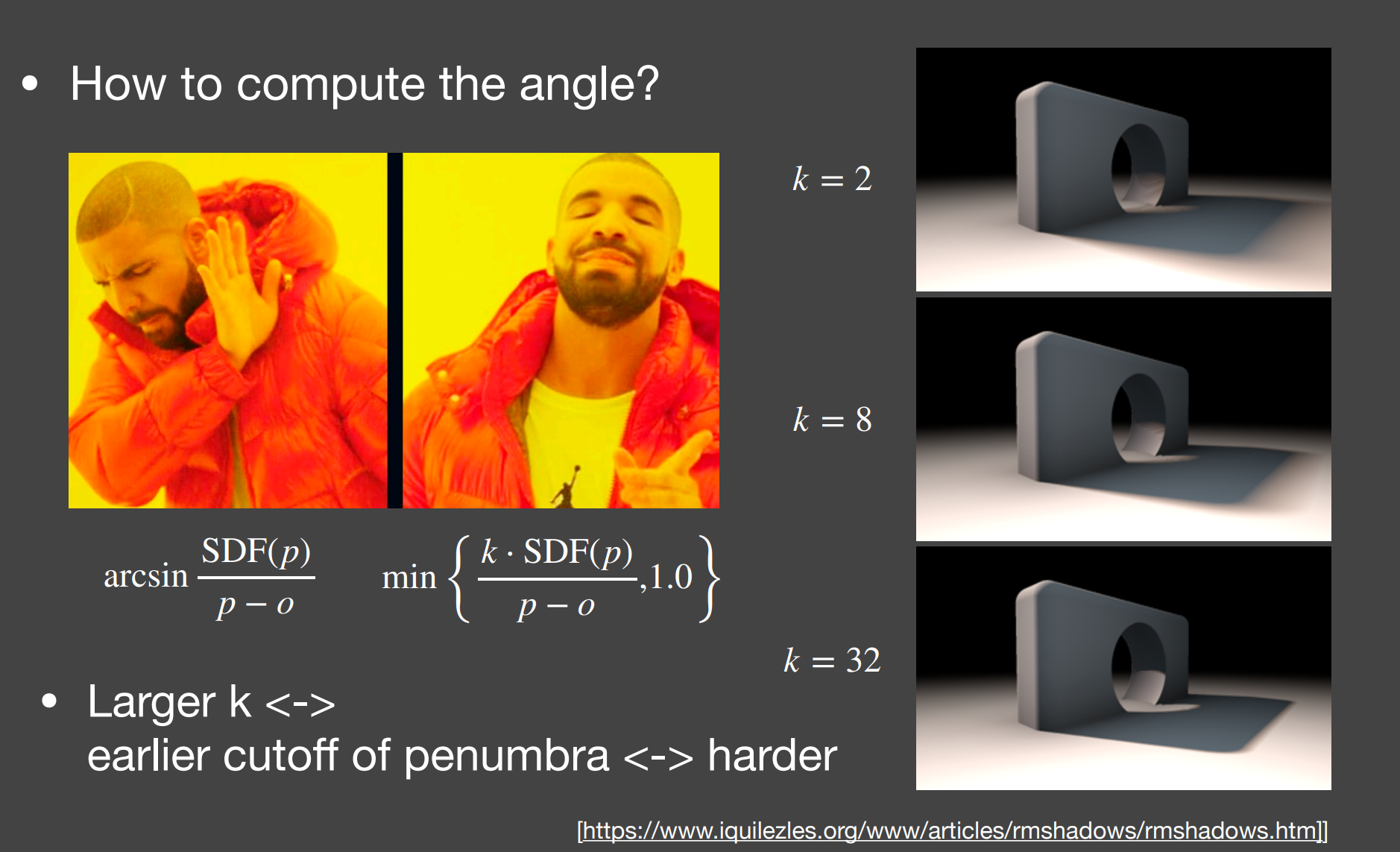
    SDF_SafeAngle

    • 因此用来替代，并用 $k$ 控制阴影的软硬程度；

f.2). Pros and Cons

  • Pros
    • 快（使用角度，不考虑生成）
    • 高质量
  • Cons
    • 需要预计算
    • 需要额外存储（不仅仅是图形，而是需要三维空间存储）
    • 对于形变物体需要大量实时计算
    • ……