Games202-3 Real-time Environment Mapping
Mesh Distance Fields,Real Shading in Unreal Engine 4
a). Shading from Environment Lighting(IBL)

- 通过环境贴图着色的方式,又被命名为 Image-Based Lighting (IBL)
a.1). How

- 对于IBL,可以看做是上半球(可以联想下UE中的HDRI)的光照和BRDF的积分;
Observation:
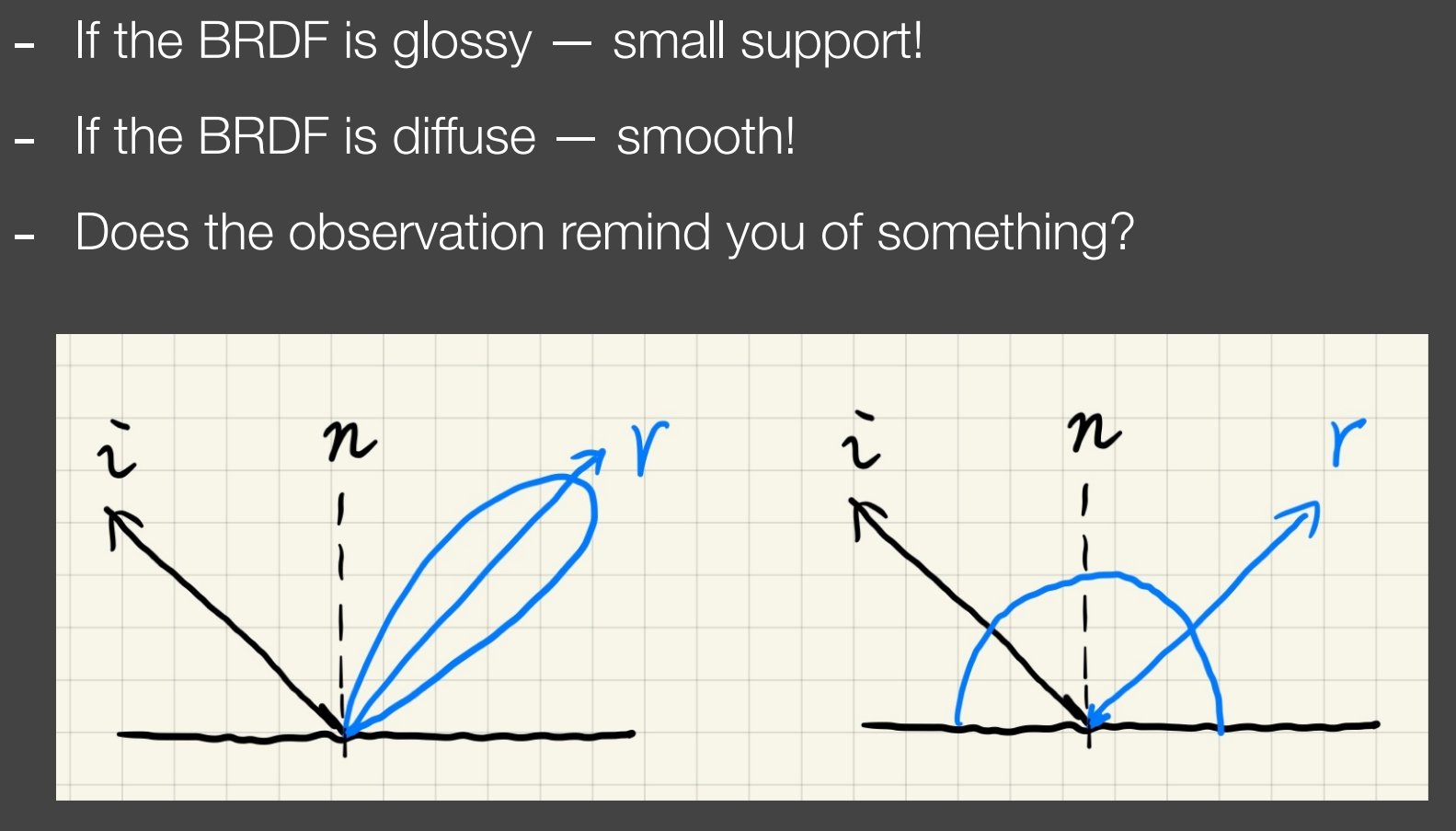
对于Glossy,其BRDF支持集很小(Lobe范围小);
对于Diffuse,其BRDF非常平滑;
联想到上节课渲染方程不等式成立的条件(拆出乘积积分的那个)
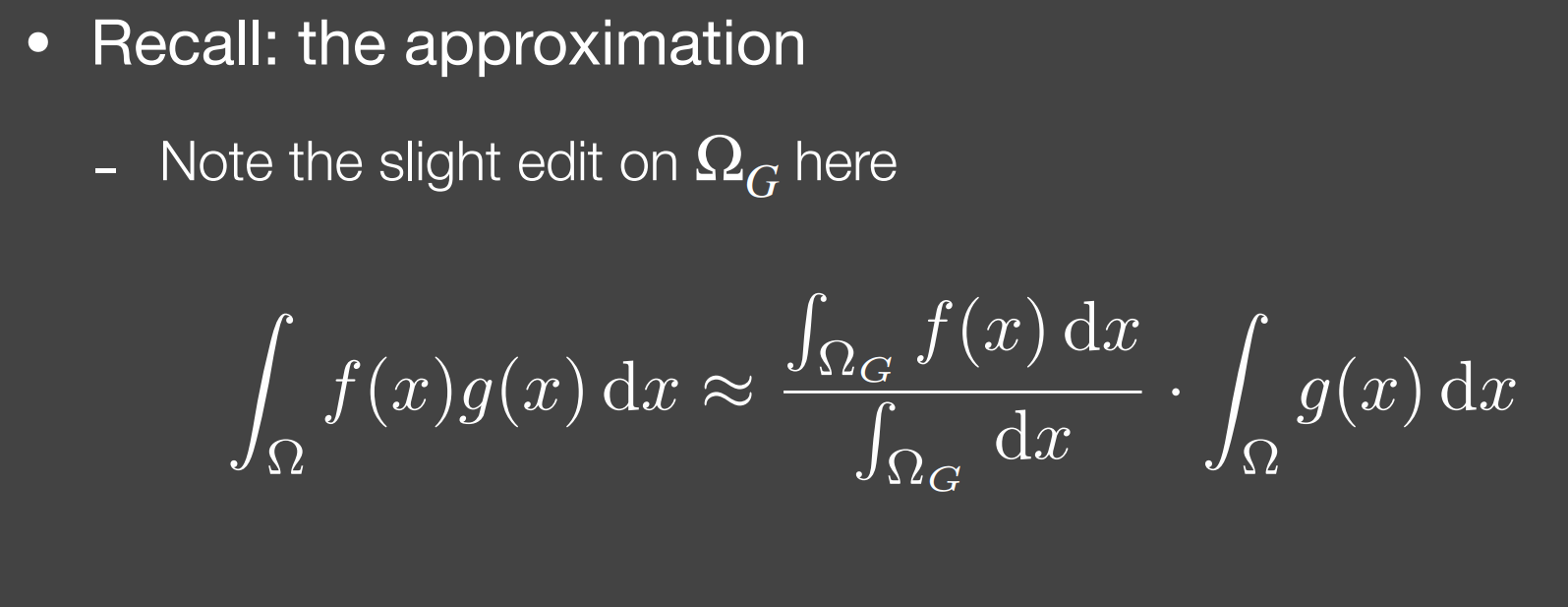
这里$\Omega_{G}$ 指积分域上,$g(x)$有值的区域。
如$g(x)$ 为BRDF,$\Omega_{G}$ 即为原点向Lobe各点出发,与积分半球相交的区域集合
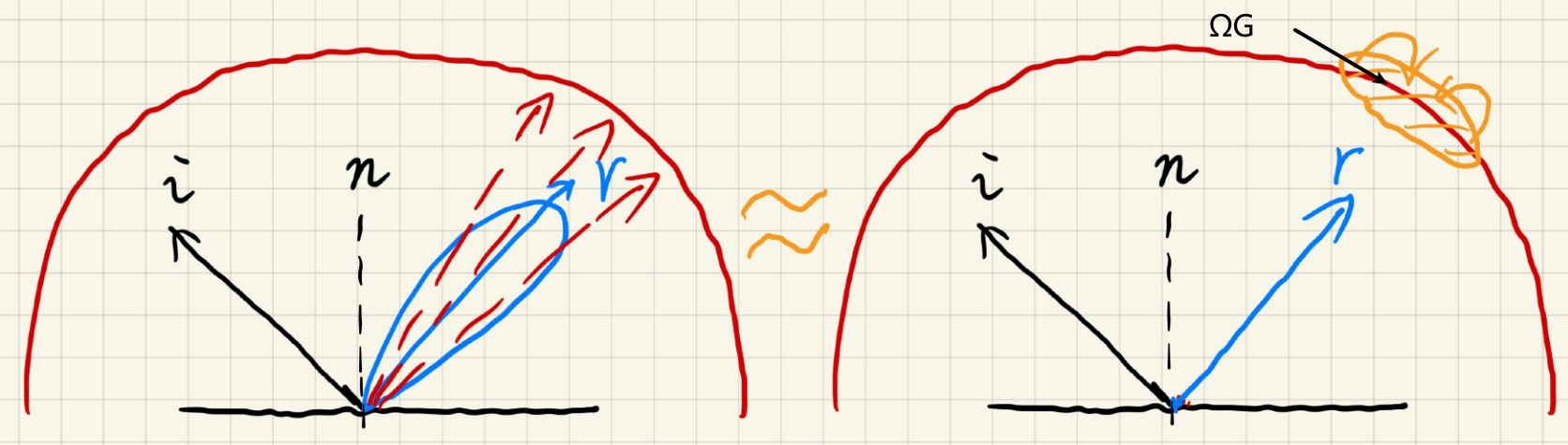
We can safely take the lighting term out!

我们把渲染方程分为了两部分积分,分别是:
- 在$\Omega_{fr}$(即Lobe对应的半球区域),对光照Radiance积分
- 在半球内对BRDF积分;
a.2). Lighting(对Radiance积分)
Lighting:
即在$\Omega_{fr}$(即Lobe对应的半球区域),对光照Radiance积分,再归一化(normalize,分母用于归一化);
类比于PCF,就是对Environment Map做滤波;

- 滤波方法:Mipmap
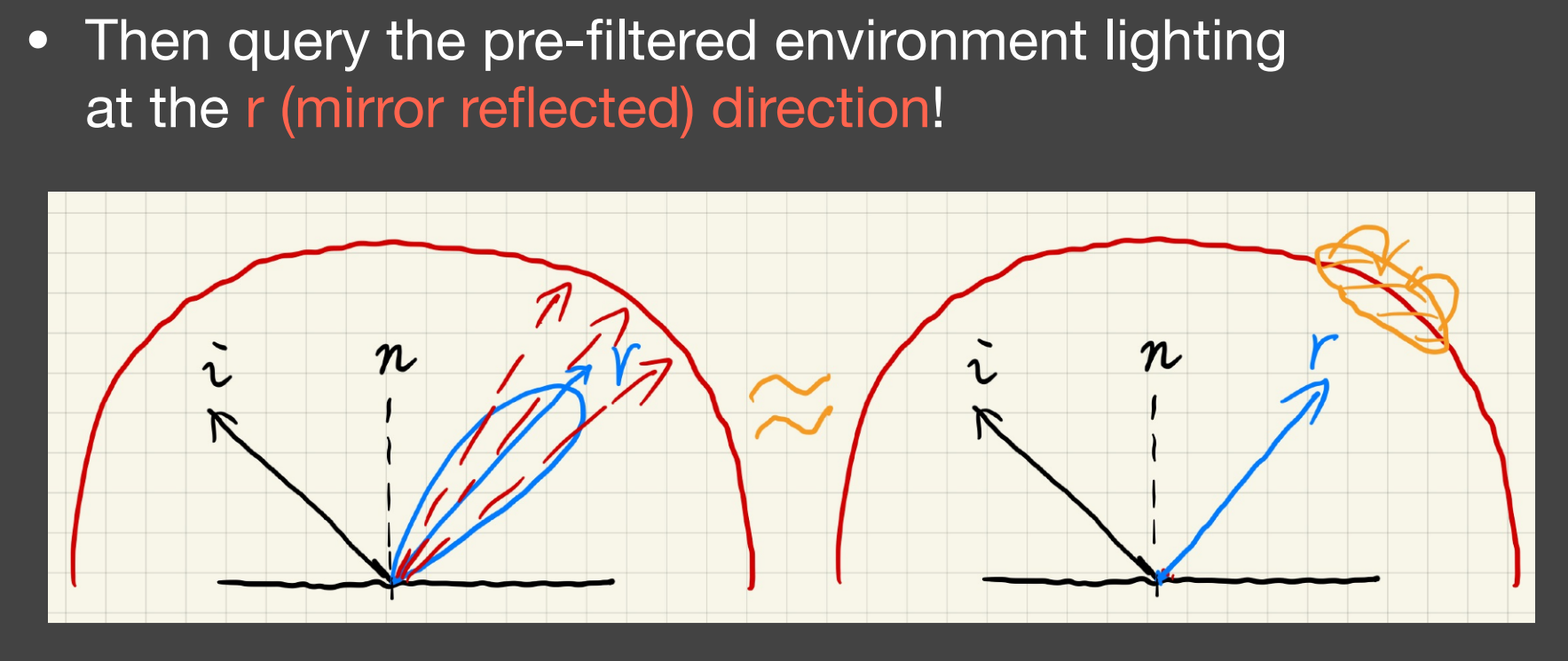
在Shading中,需要获得Lighting项的值,只需要求得Environment Map对应Mipmap层,Lobe中点(镜面反射方向)方向的结果
- 和百人计划图形2.5中,做Relief Mapping时在Unity用到的texCUBElod(),对Mipmap采样联系上了;
1
fixed3 Reflection = ACESToneMapping(texCUBElod(_CubeMap, float4(worldRef, (255-_Gloss)*8/255)).rgb, 1) * SpecularTint * _EnvIntensity;
a.3). 对BRDF积分(Split Sum)

假设使用微表面理论的BRDF
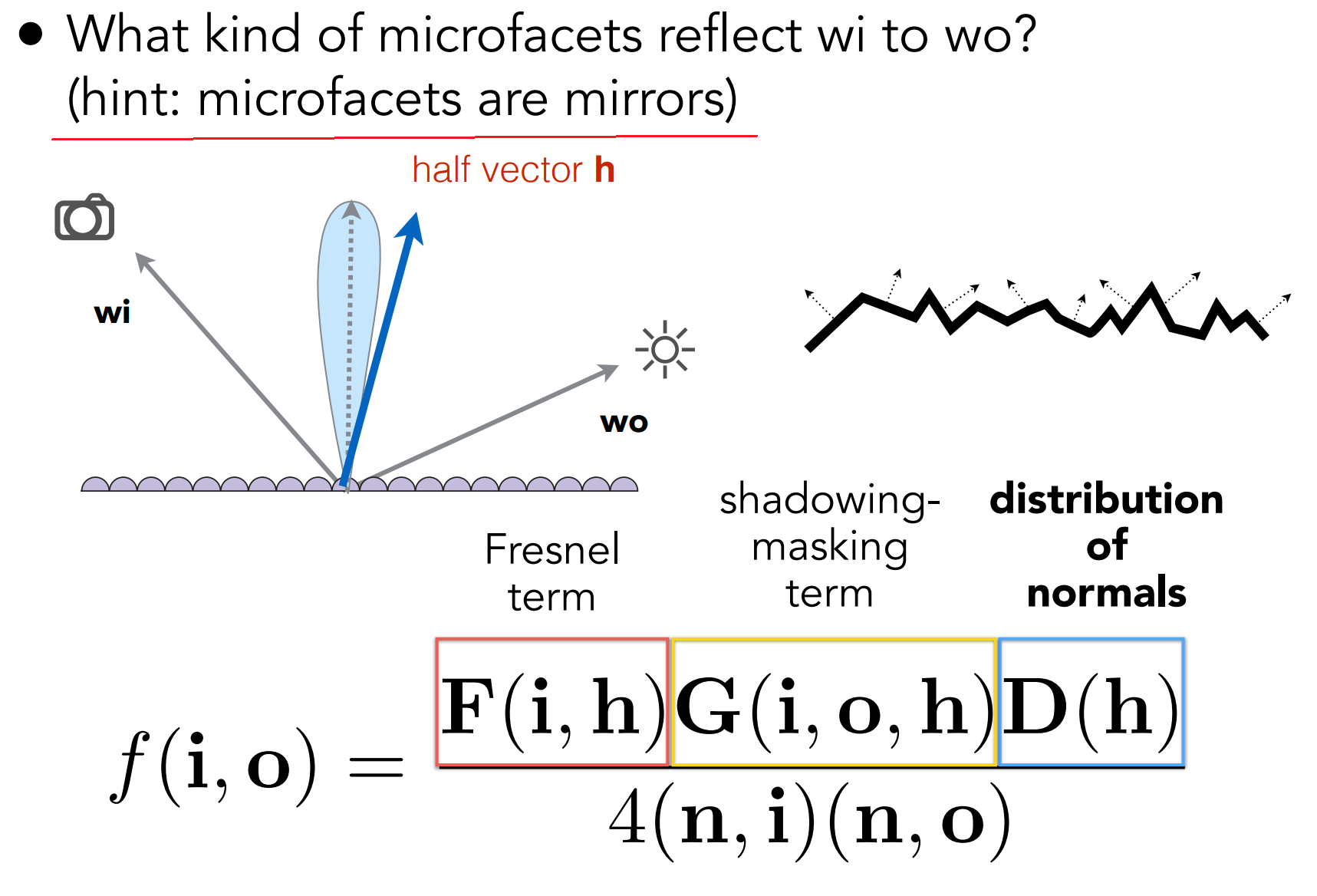
- 做法: 预计算考虑进所有变量(roughness、color等)的可能值的积分;
- 但是,维度过高,存储成本过高,因此需要降维;
降维过程:
对应微表面BRDF,只考虑Fresnel term($F(i,h)$)和distribution of normals($D(h)$)
Fresnel term采用the Schlick’s approximation
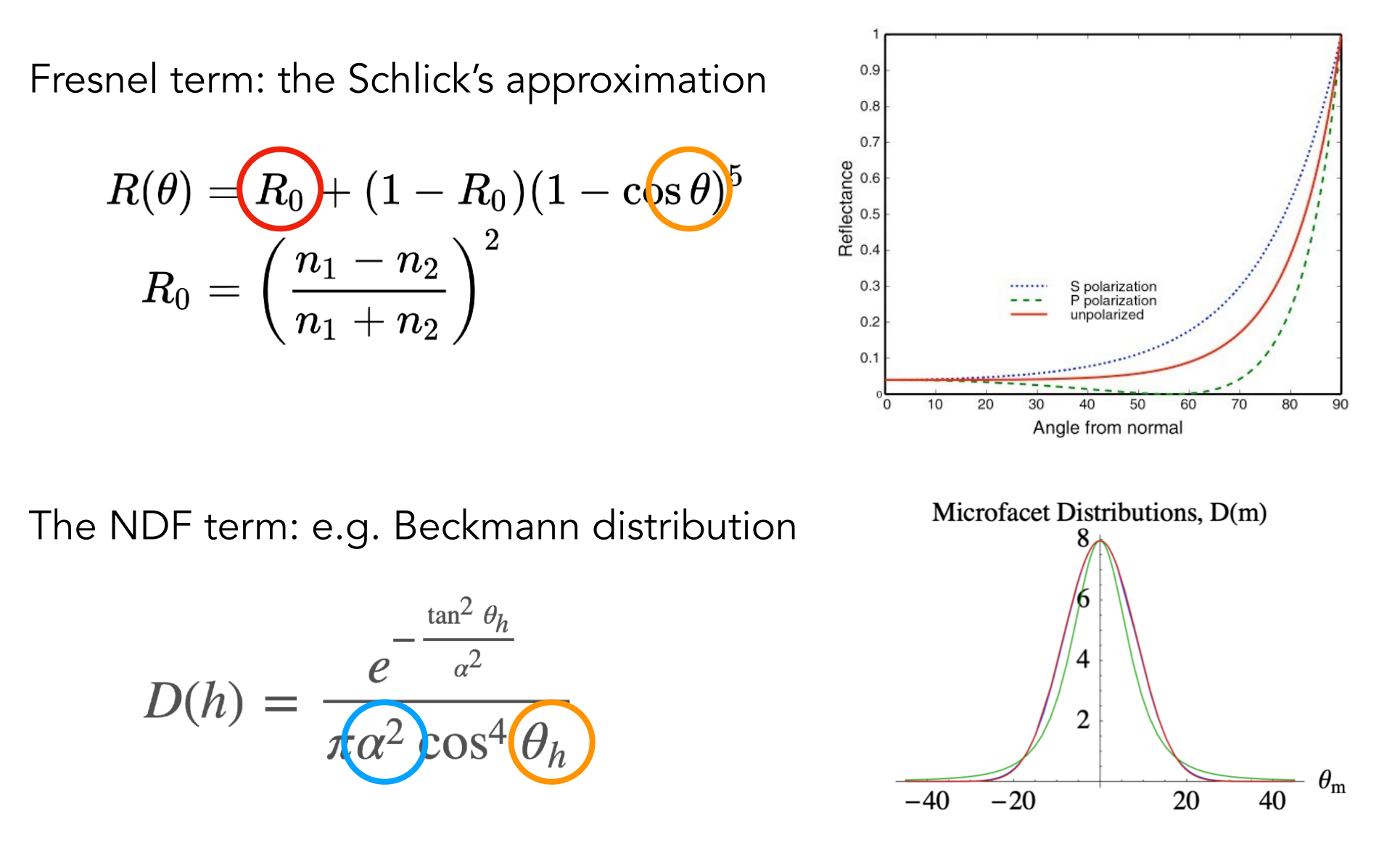
- 至此,积分降维为三维
- $R_0$ :零度菲涅尔值
- $\alpha$ :可表示为roughness,$\alpha$ 越大,越粗糙;
- $\theta(\theta_h)$ :在实时渲染中,我们认为出射角、入射角以及入射角/出射角与半程向量的夹角,这三者是相同性质的(不是说值近似相等,而是指作为积分的元素效果相同)
- 至此,积分降维为三维
在对BRDF的积分式中,通过Schlick’s approximation,将$R_0$拆出,即写成下列式子

- 积分现在被降维为二维($R_0$被拆出,$f_r$中的菲涅尔项被分母抵消)
- $\alpha$
- $\theta$
- 积分现在被降维为二维($R_0$被拆出,$f_r$中的菲涅尔项被分母抵消)
至此,我们对积分的两项分别进行预计算,储存在表格或者图片中(R、G通道分别两项积分结果)通过LUT查询即可

- 而$R_0$ 则可通过BaseColor(Metallic Workflow)、Specular(Specular Workflow)贴图或软件内置(一般默认为4%)即可获得;(看百人计划美术 2.7 Metallic与Speculer流程)
名字由来: Split sum

假设使用Lambert的BRDF
- $f_r = {1\over \pi}$
- $\int_{\Omega^+}cos\theta_i d\omega_i = \pi$ (看Games101 Lecture 17-18 Materials二重积分)
- 所以正好BRDF积分为1
b). Shadow from Environment Light
在实时渲染中,没有完美的解决方案;

- 难以用实时渲染方程(那个不等式)来近似:
- Support大,为整个半球
- 带有Gloosy项,不够smooth
- 难以用实时渲染方程(那个不等式)来近似:
工业界方法:
- 只计算最亮的灯光(如UE中HDRI带一个Direction Light)
- Related research
- Imperfect shadow maps
- Light cuts
- RTRT (Real-Time Ray Tracing, might be the ultimate solution)
- Precomputed radiance transfer(PRT)
c). Spherical Harmonics(SH, 球面谐波函数)
c.1). 前置知识
Fourier Transform
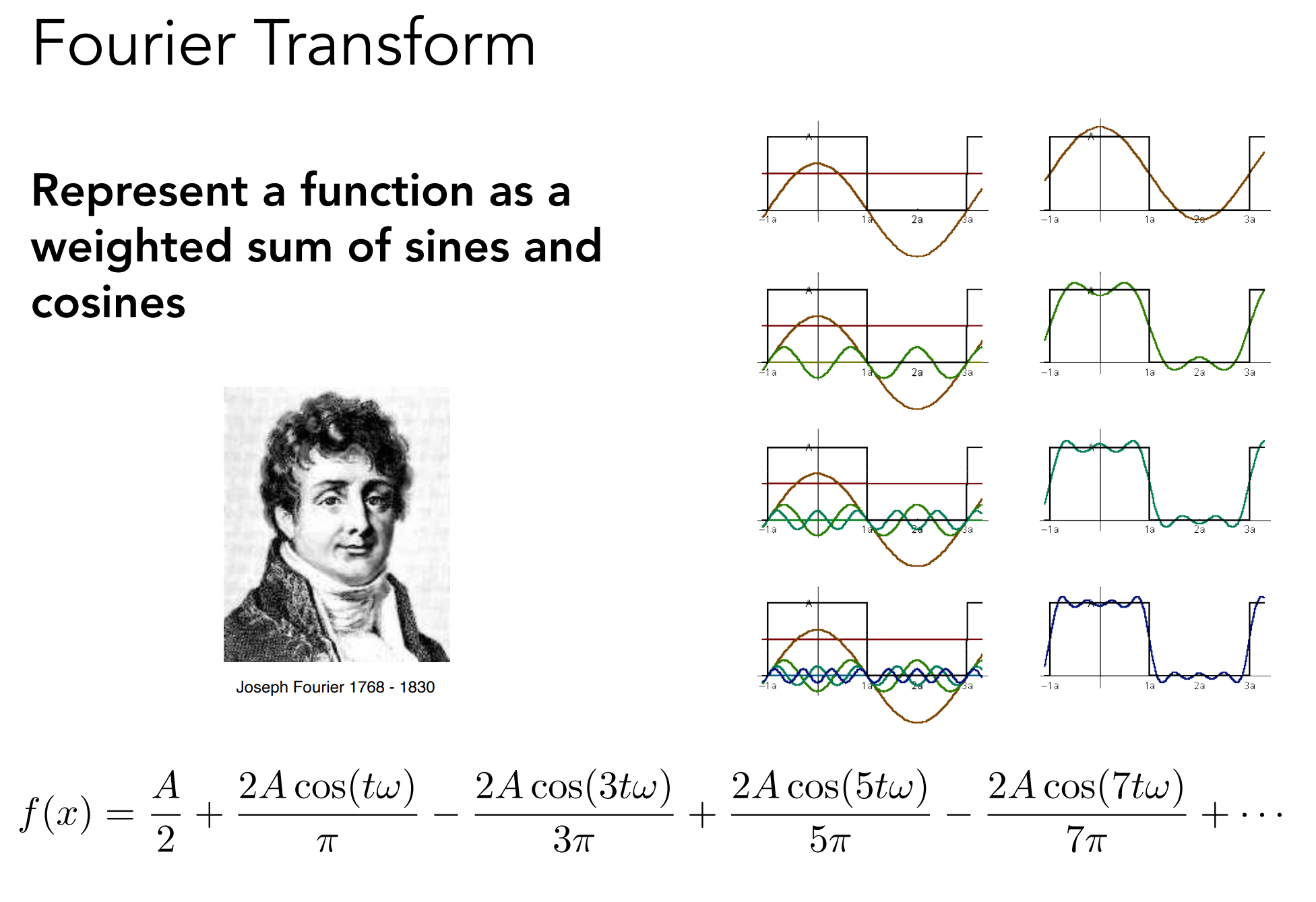
这里是偶函数,所以 $sin$ 项系数都为0

Convolution Theorem
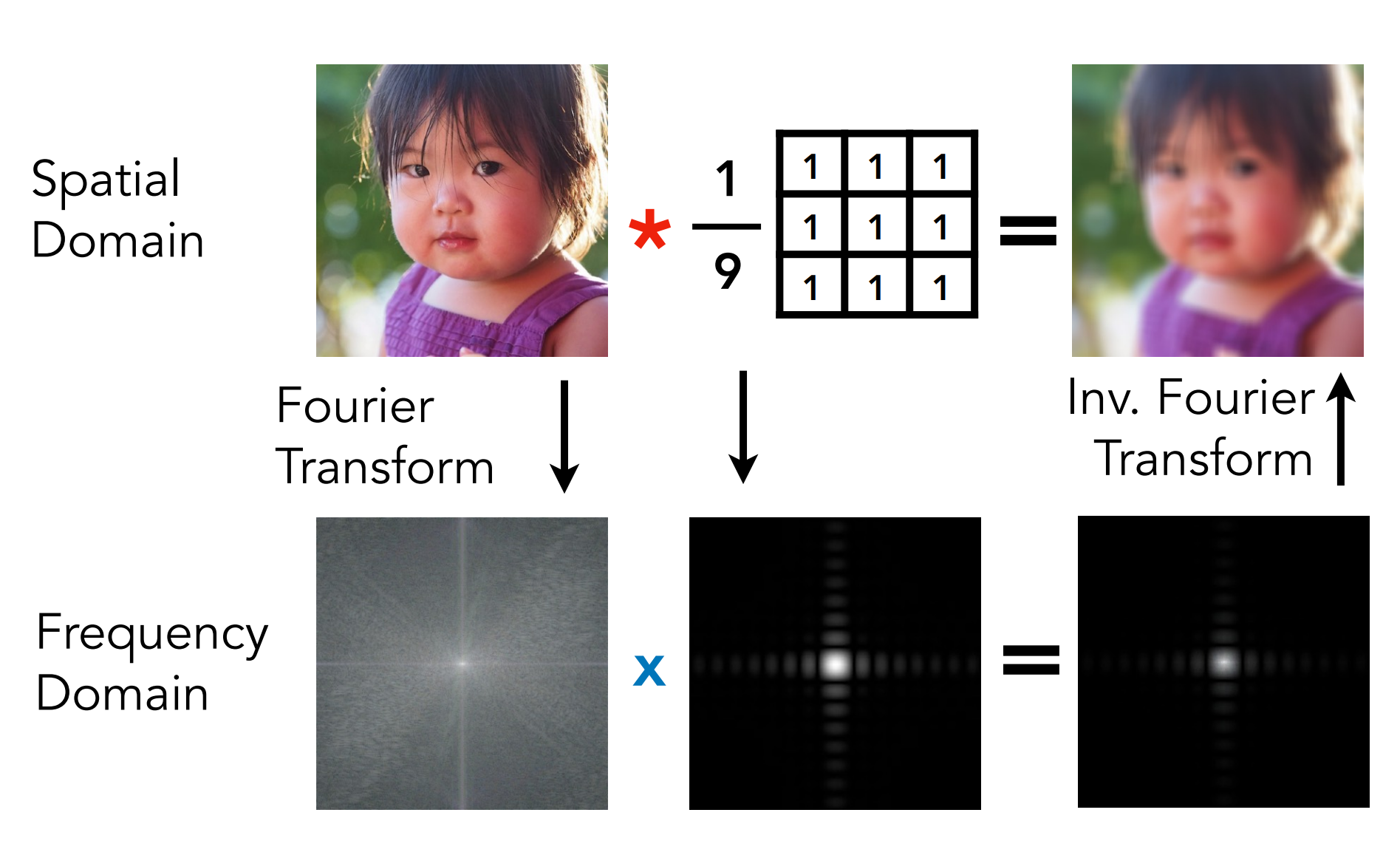
- 时域卷积等于频域乘积
A general understanding

product intergral: 相乘后积分,对应离散的情况就是相乘后相加。如:
$n$维向量$\bold{a} = (x_1, x_2,…,x_n)$ 和 $\bold{b} = (y_1, y_2,…,y_n)$ 进行product intergral,即点乘
$\bold{a} \cdot \bold{b} = x_1y_1+x_2y_2+…+x_ny_n$
我们认为,函数相乘后积分(product intergral),就是滤波(卷积)
- 积分结果的频率,取决于频率最低的项($f(x),g(x)$)
Basis Functions(基函数)

- $c_i$ 为系数
- 如傅里叶变换中,各项就为正交基;
- 或者多项式和泰勒展开等
c.2). 简介
What?
球谐函数 是一系列 二维球面函数的正交基函数
- 球谐函数具有正交、归一、完备性
如
$f(\omega)$ 为球面函数,$\omega$ 为向量
$c_i$ 为系数
$B_{i}(\omega)$ 则为球谐函数

- 说明:
- 每一行($l=n$),频率相同
- 对于$l=n$行(第$n$阶),函数数量为$2l+1$
- 每一阶各SH都有编号,即$m$ 从$-l$ 到 $l$;
- 说明:
How?
每一阶的SH函数,由勒让德多项式求得;
如何求得$c_i$
投影(Projection)
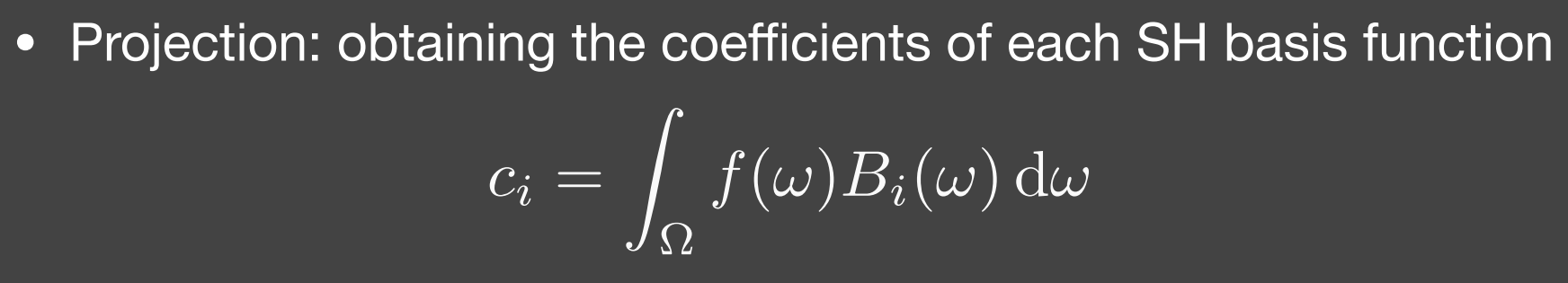
- 类似于傅里叶展开中,函数和各个正交基相乘求系数
c.3). 性质
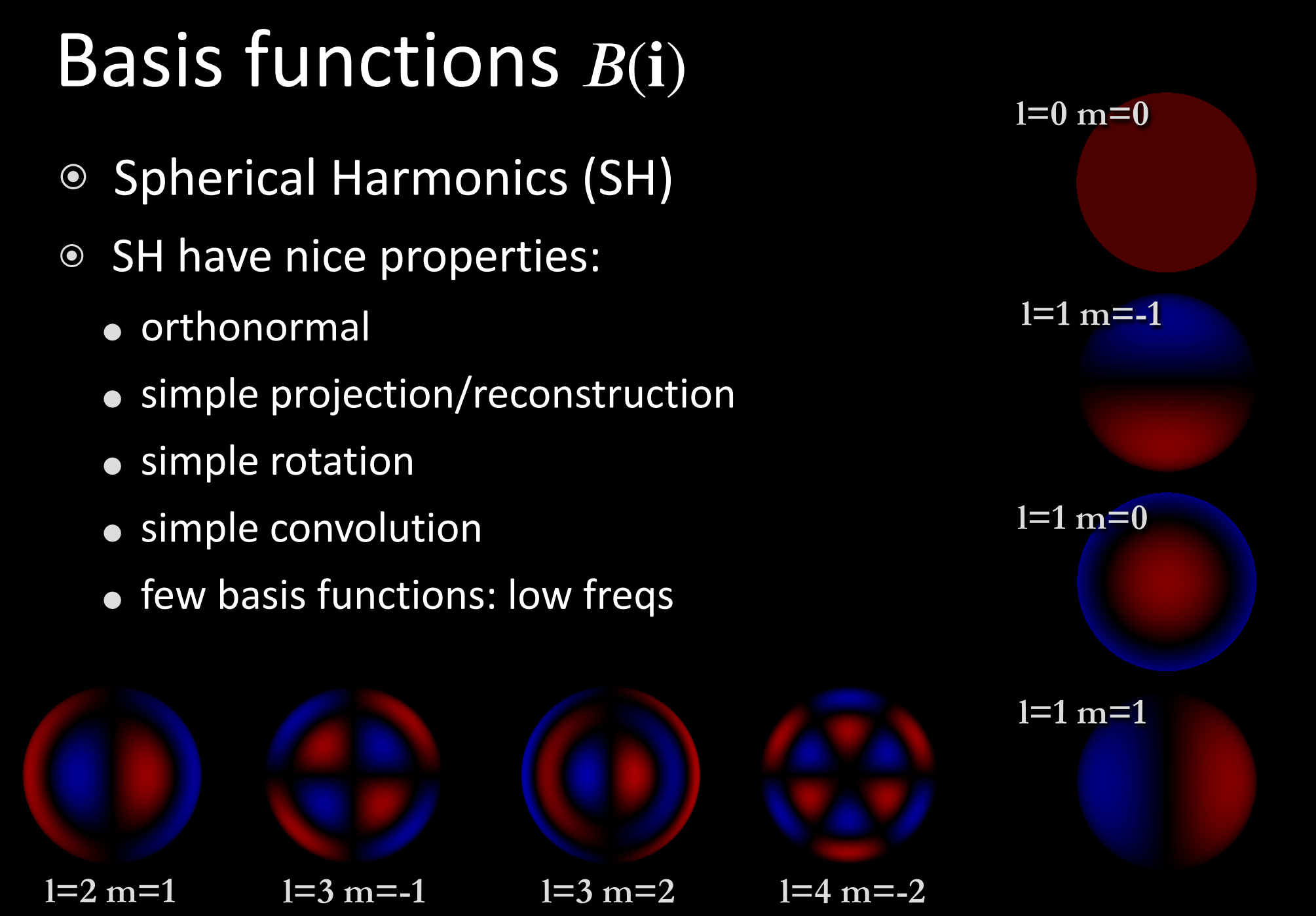
- 正交性;
- 投影性;
- 旋转方便(旋转$f(x)$,相当于旋转基函数$B(i)$)
- SH中,旋转后的基函数,可通过同阶的基函数线性组合得到;
d). Shading from Environment Lighting(SH, Diffuse项)
d.1). 简介


- 如果不通过IBL方式,计算shading,那可以通过SH展开$L_i(p,\omega_i)$ ,即展开Environment Map(Environment Map可以写成二维函数)
d.2). 分析Diffuse项的BRDF
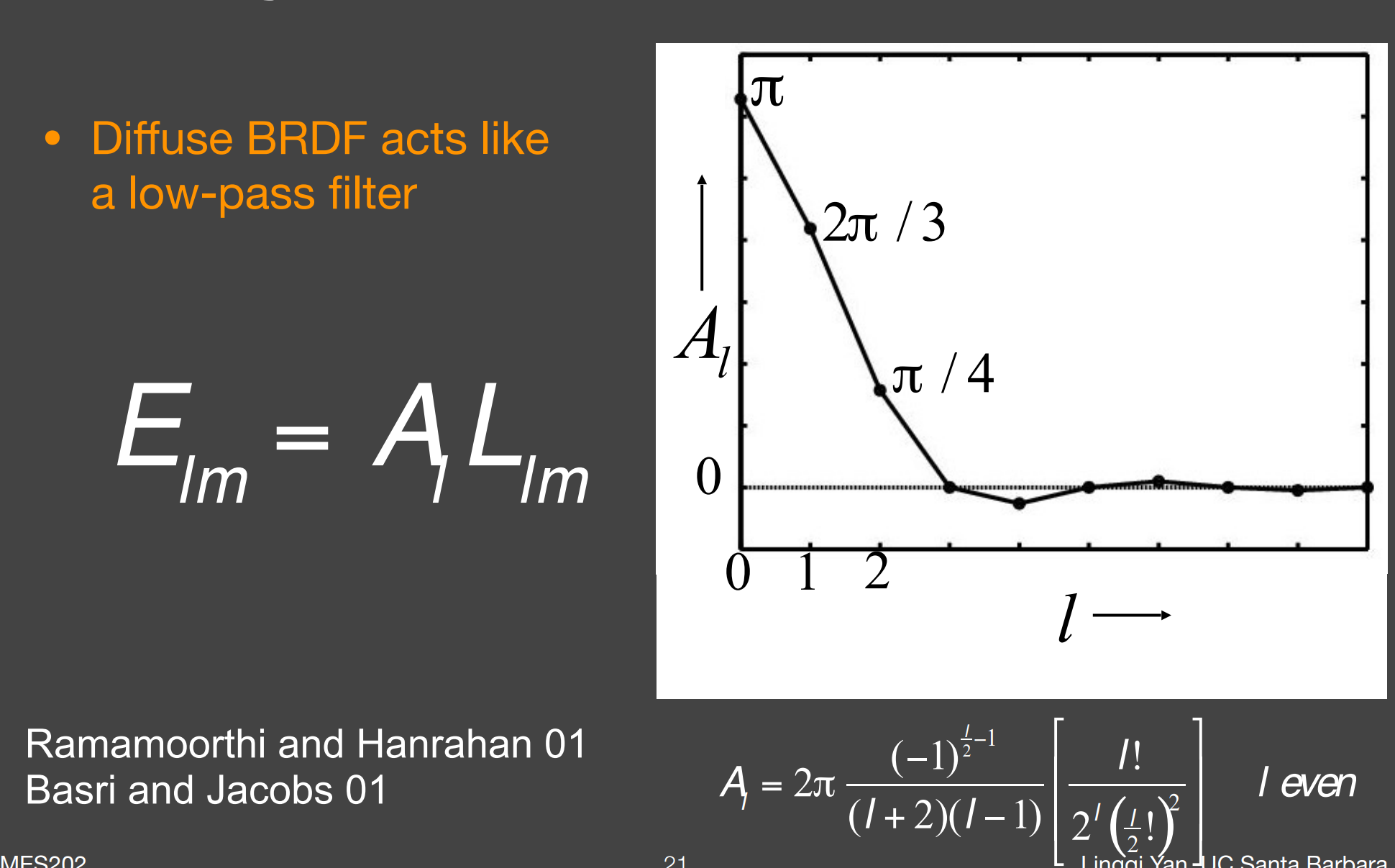
- $A_l$ 就是基函数的系数;
- 由图可见,通过SH分析Diffuse项的BRDF后,可得出结论
- 当$l\geq3$ (即第四阶开始),其 $A_l$ 接近0,说明Diffuse项的BRDF频率低,由SH前三阶表示即可;
积分结果的频率,取决于频率最低的项($f(x),g(x)$)
- Diffuse BRDF acts like a low-pass filter
- 因此,对于Environment Map的展开,只需要SH前三阶即可
d.3). SH展开Environment Map


- 通过求得各球谐函数的结果后,再通过结果逆变换得到Shading结果
- 通过ShadingPoint法线,再经过一系列计算(?)得到shading
e). Precomputed Radiance Transfer

- 对于渲染方程,如果我们把它每一项都进行Brute-force(蛮力)计算
- $L_i$ : 二维,方位角$\omega$和俯仰角$\theta$
- $V(i)$ : 二维,方位角和俯仰角
- $\rho(\mathbf{i}, \mathbf{o})$ : 四维,入射角和出射角的方位角和俯仰角
- 存储压力过于大;
e.1). PRT
- 前提: 假设场景中除了Lighting,其他都不变;

- 将RE分为两项,
- Lighting变化;
- light transport不变;
- $V(i): $ 二维,$\omega,\theta$,可烘焙为图像,如CubeMap(场景摆放固定)
- $\rho(\mathbf{i}, \mathbf{o}): $ BRDF
- Diffuse Case: 常数
- Gloosy Case: 四维,$\omega_{i},\theta_i, \omega_o,\theta_o$,入射和出射的方位角和俯仰角(相机固定,入射角固定)
e.2). Diffuse Case

此处(图形学中,大部分情况都是),积分和求和位置可变;
经过预计算后,求得Shading结果只需要在SH空间中,对向量进行点乘即可;

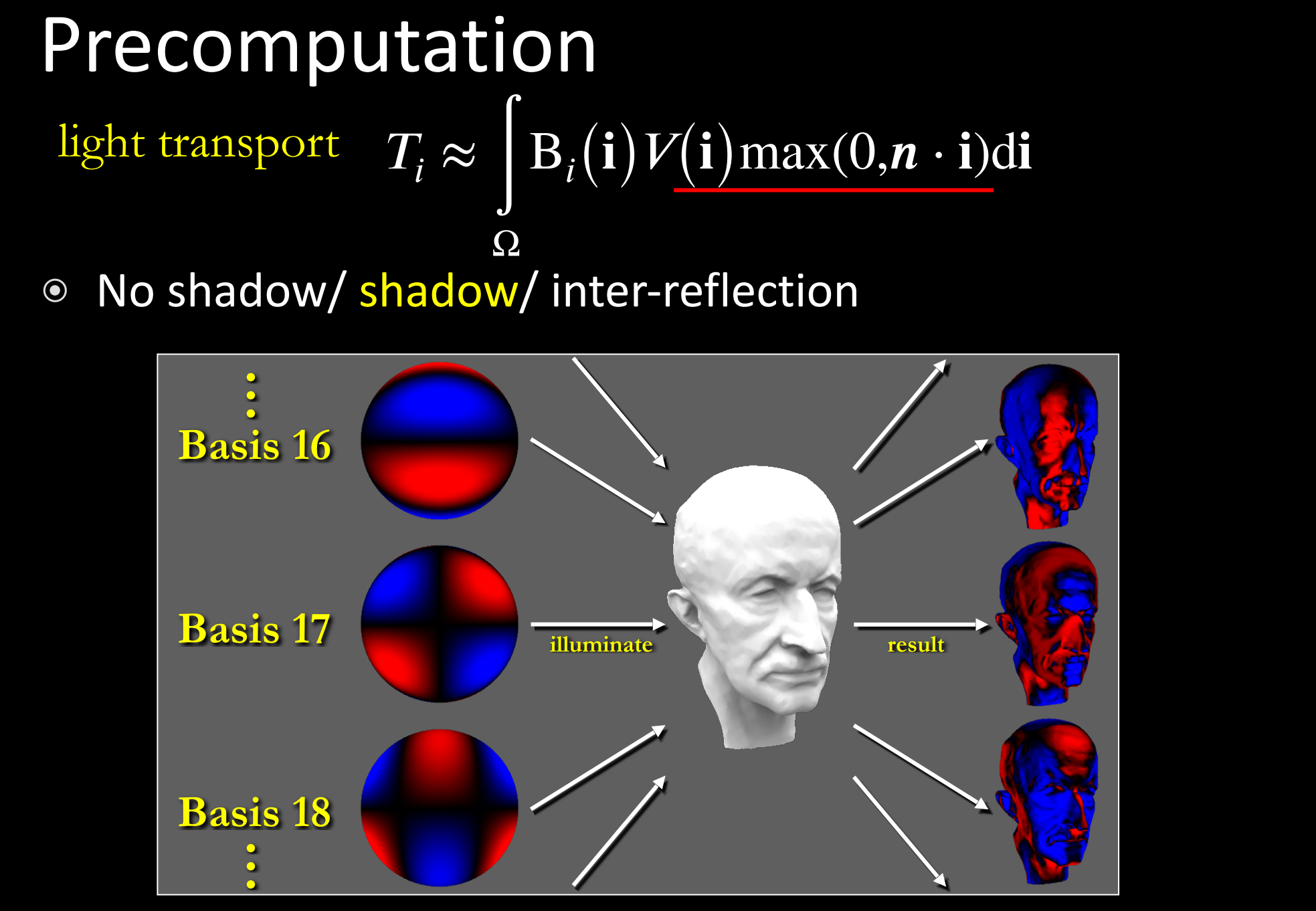

e.2.1). 计算


- 注意: 此处两次求和复杂度仍然是$O(n)$,因为SH基函数具有正交性;
Runtime is independent of transport complexity

计算Light Transport简易理解: 积分形式和渲染方程相似,$B_i(\bold{i})$ 类似于$L_i(\bold{i})$ ,可看成是将球谐函数作为光照进行Shading得到Light Transport结果
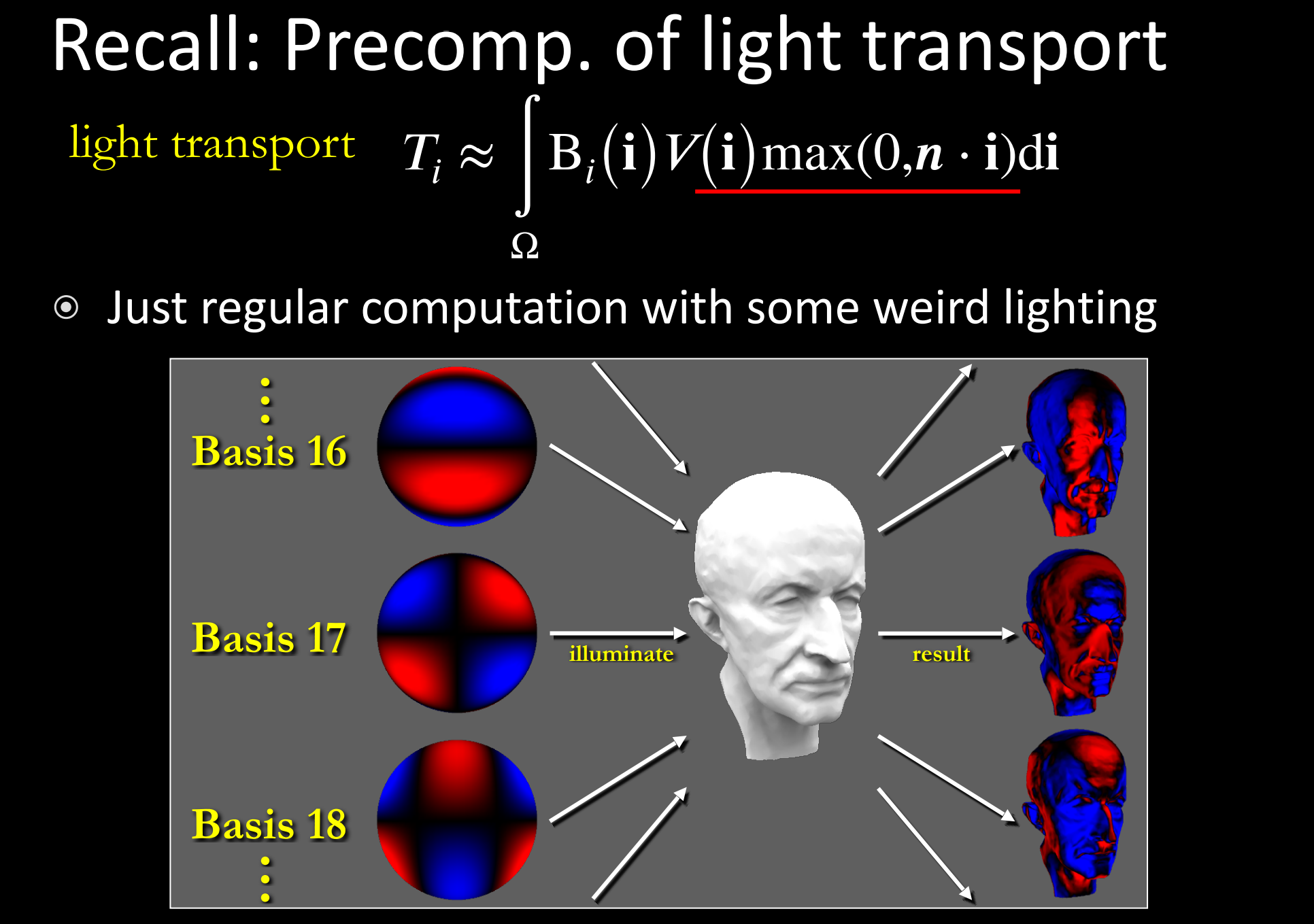
e.3). Glossy Case
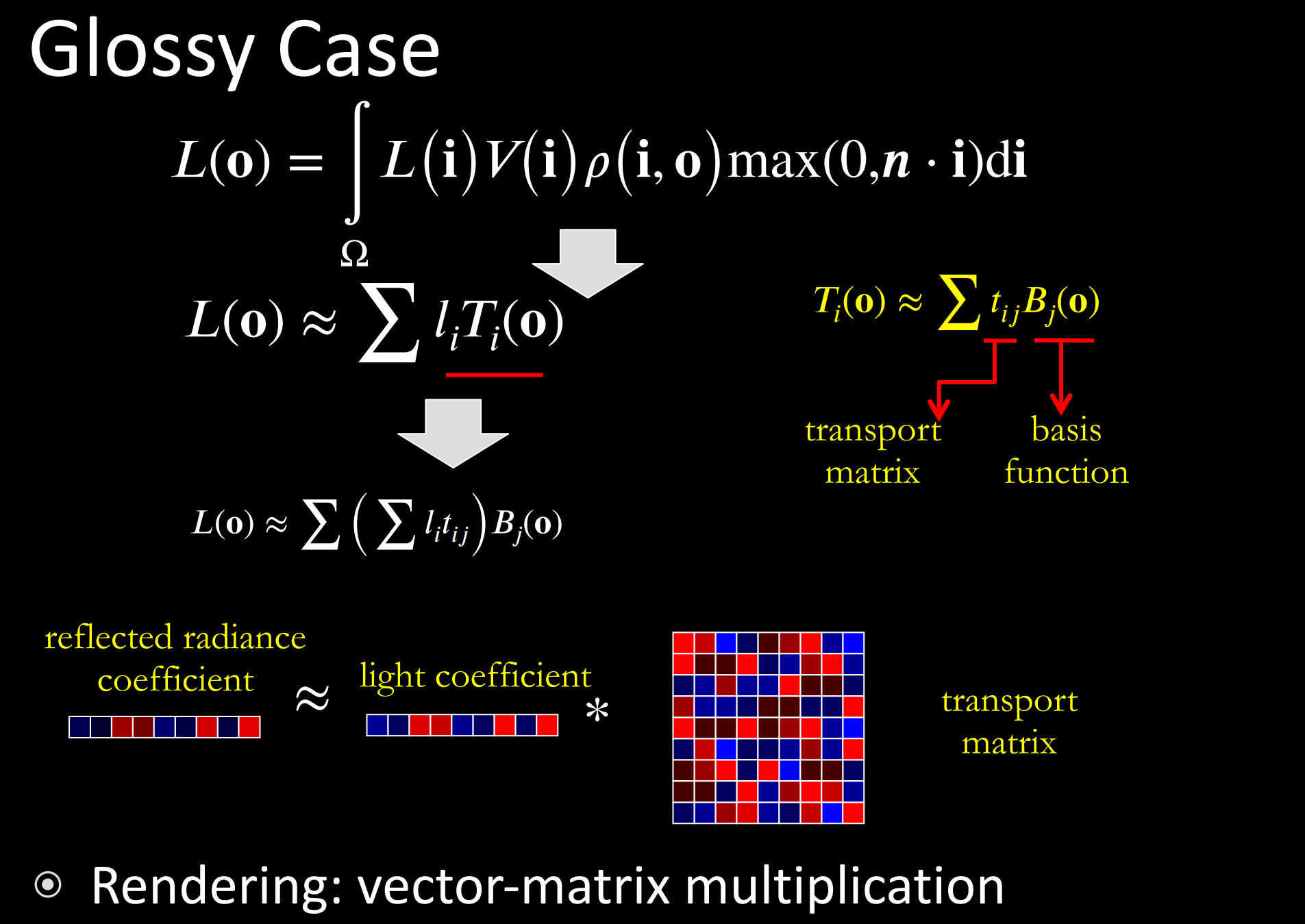
- 此时,BRDF是关于入射和出射的方位角和俯仰角的四维函数;
- 做法: 对 $\bold{o}$ 也进行SH展开;(对于Gloosy不止展开到第三阶)
- light coefficient与Diffuse Case相同,为SH空间的一维向量;
- transport matrix则是关于 $\bold{o}$ 和 $\bold{i}$ 四维函数(入射和出射的方位角和俯仰角),为SH空间的二维矩阵;
- reflected radiance coefficient则是关于 $\bold{o}$ 的二维函数(出射角的方位角和俯仰角),通过SH逆变换,即可得出相应视角( $\bold{o}$ )下的Gloosy radiance;
- 具体怎么变换的?待实现
e.4). 总结和限制


f). Wavelet(小波)
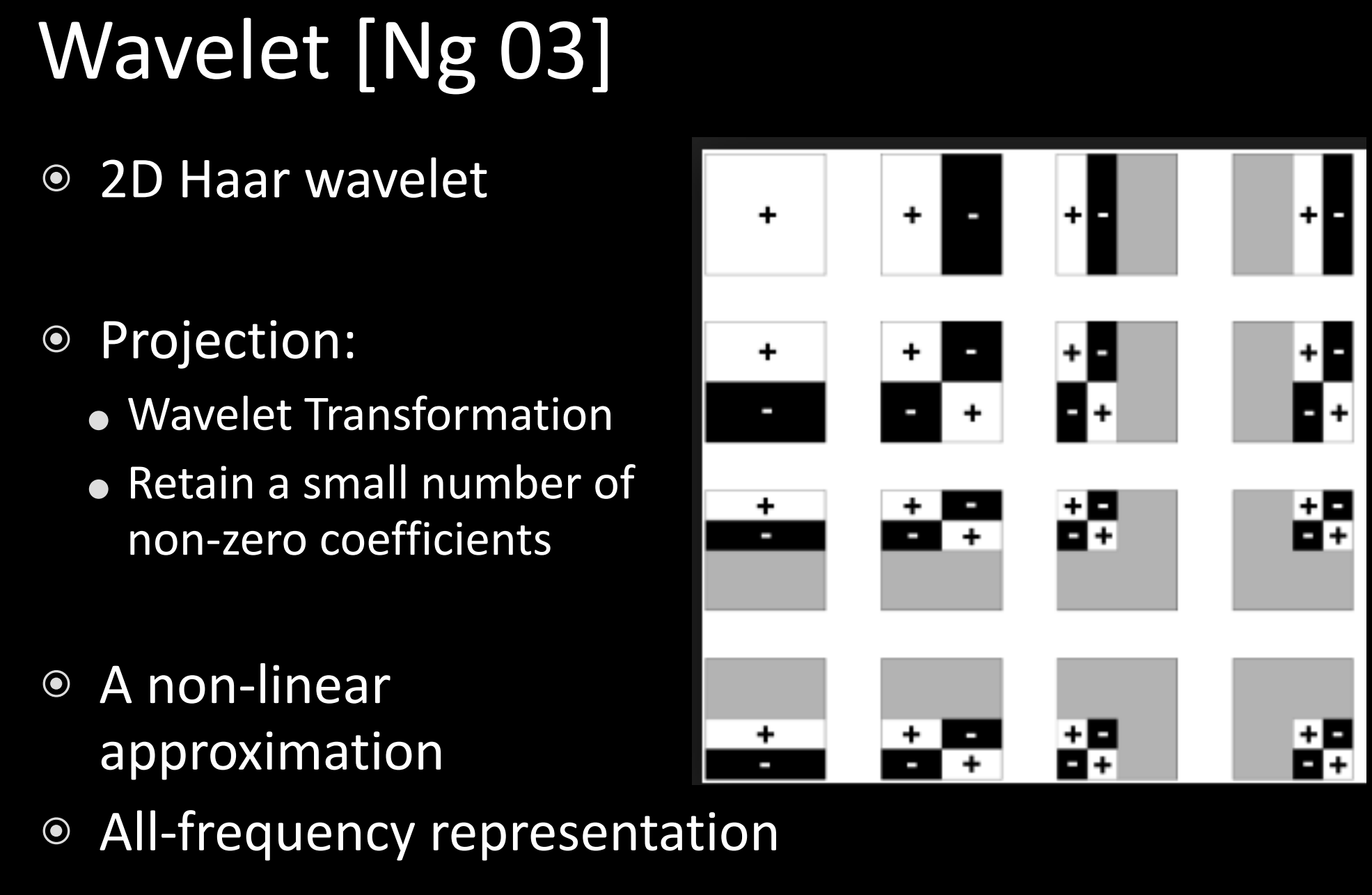
定义在二维平面上的一系列基函数
A non-linear approximation: 二维函数经过小波变换后,大部分系数接近0,这时可采用只记录系数大于一定值的项来近似原函数;

- 对于Environment Map,小波变换无法变换球面函数,因此展开为Cubemap后进行小波变换;
- 每一个矩形经过小波变换后,把高频信息放在右上、右下、左下子块,剩下的低频信息放在左上,继续做小波变换;
其他应用:JPG格式图片压缩, 使用类似与小波变换的DCT(Discrete cosine transform,离散余弦变换)、JPEG2000
效果对比:

缺点:
- 旋转不方便(不同于SH基函数的旋转简易型,小波旋转需要从Wavelet展开,旋转后再做小波变换)