Games202-5 Real-time Physically-based Materials

发表于 更新于 分类于 阅读次数：

Q1：在金属或高光工作流中，对于非导体材质（电介质）默认其零度菲涅尔值$R_0$ 为4%，那么按PBR来，他怎么会有颜色呢；还是说非导体的albedo就是$R_0$ ? 按作业中来好像albedo就是 $R_0$ ，后续还得深挖一下；

Q2：Jacobian 项，方向导数需要去了解更多

a). Introduction

PBR_Intro00

  • 尽管实时渲染中的PBR，不一定完全基于物理。如Disney principled BRDFs (artist friendly but still not PBR)

b). Microfacet BRDF

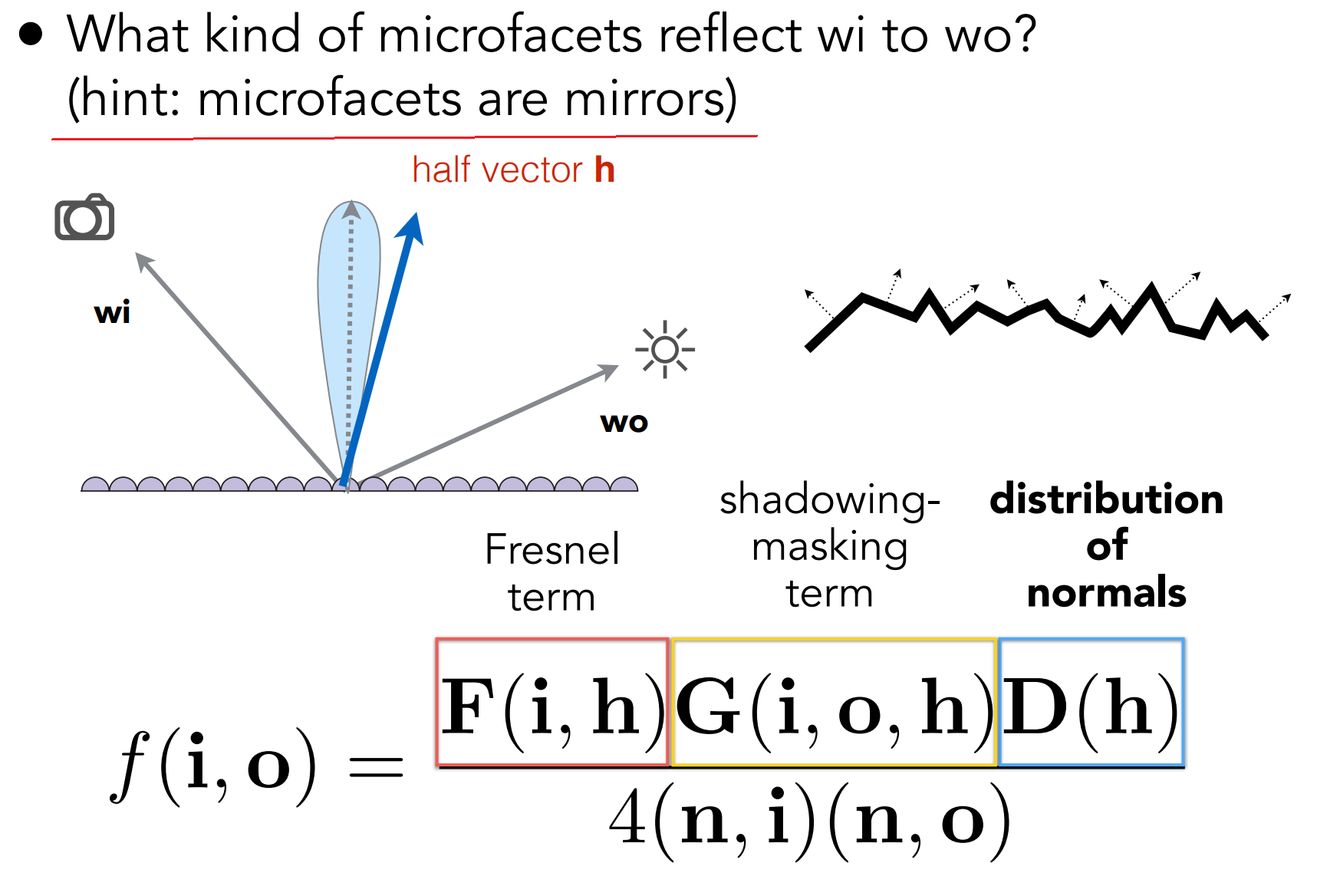
MicrofacetBRDF

  • 菲涅尔项；
  • Shadowing-masking term
    • 考虑微表面之间的遮挡和阴影；
    • 当光线几乎平行与表面入射时(Grazing angle)，微表面之间遮挡变多
  • Disterbution of normals(法线分布)

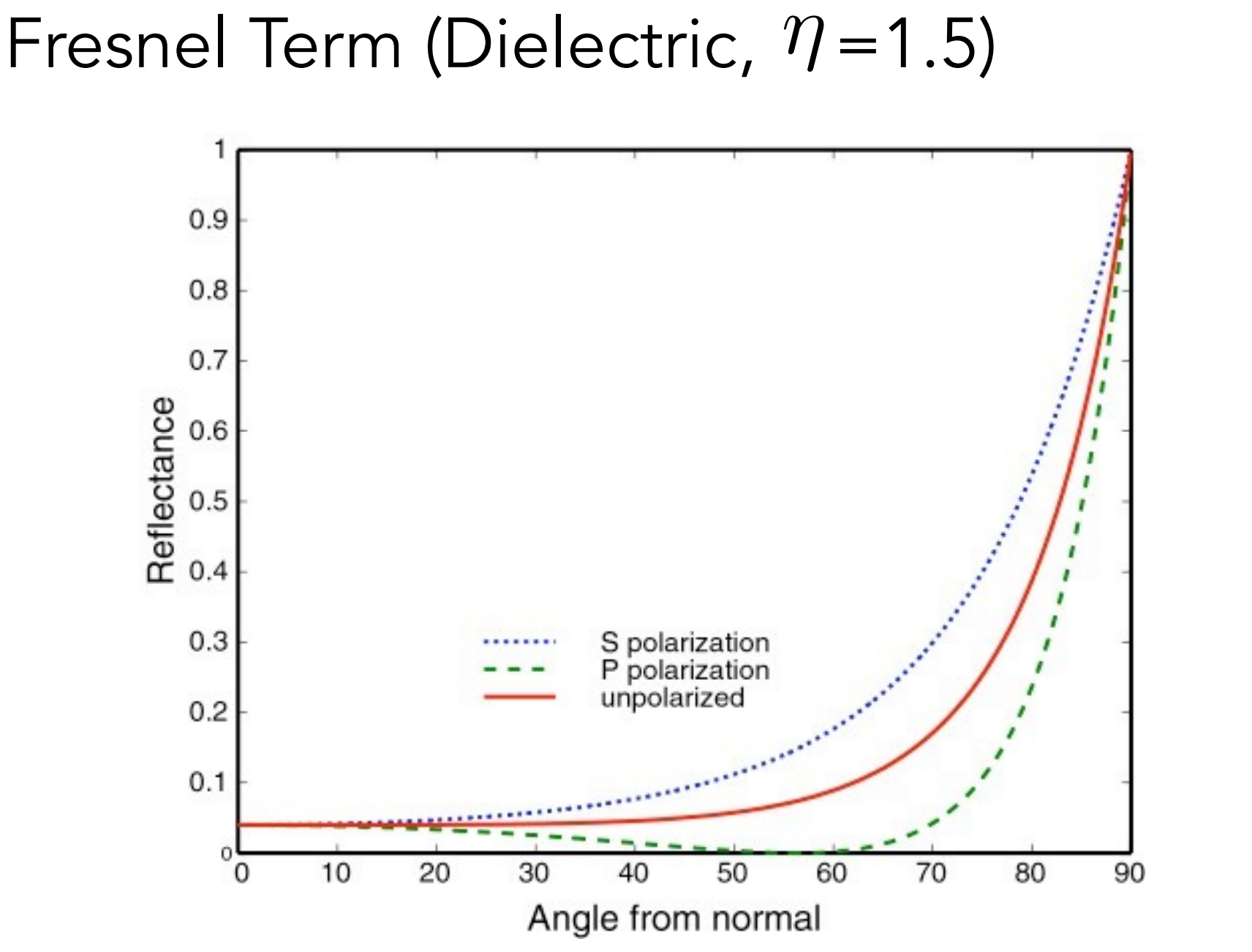
b.1). The Fresnel Term

  • 本质上是考虑能量的吸收和反射（即考虑BRDF就会有因为颜色的合理的能量损失）
绝缘体_Fresnel
导体(金属)_Fresnel

FresnelTerm

b.2). Normal Distribution Function(NDF)

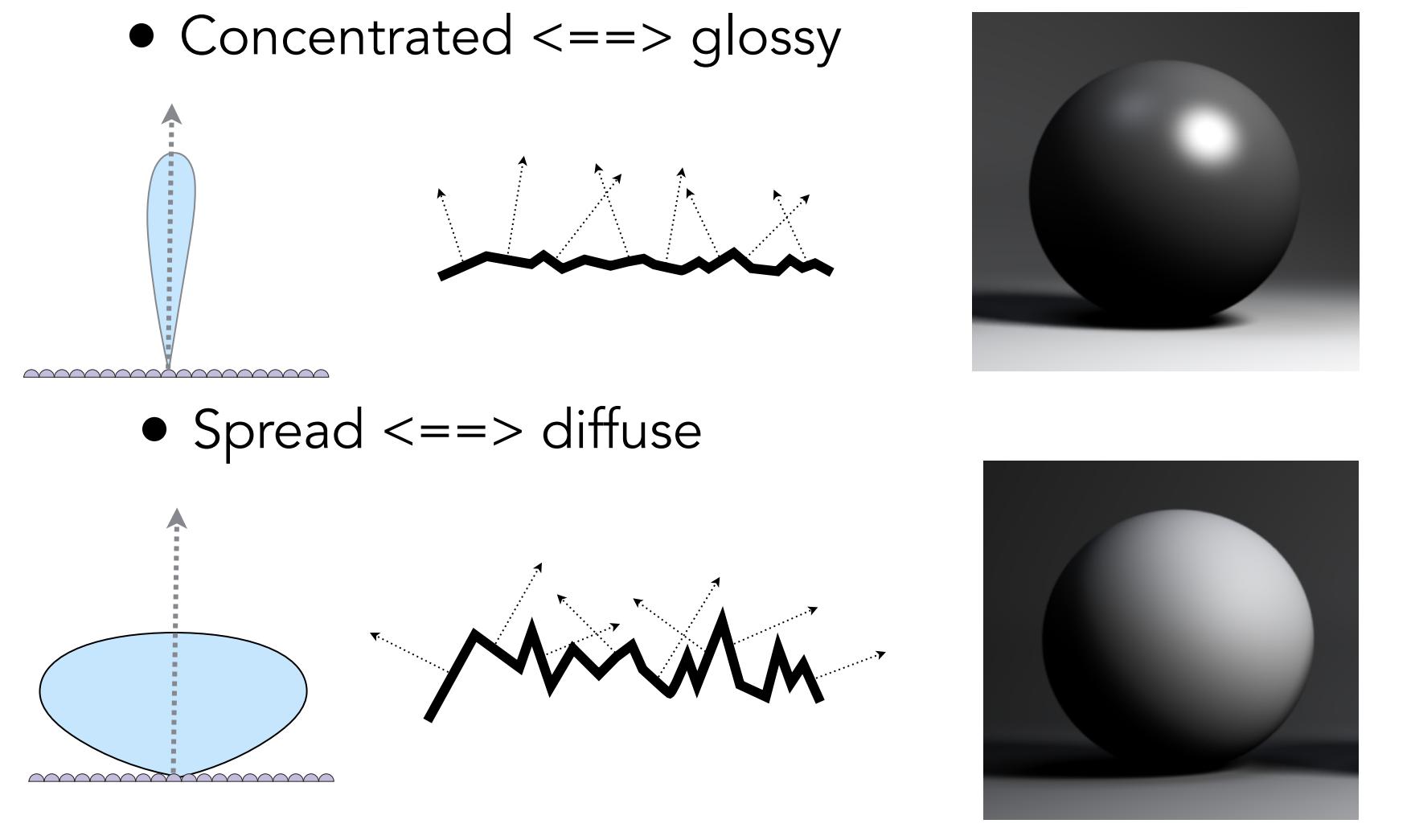
NormalDistribution

  • NDF从简单（如Gloosy）变为复杂（如Diffuse），就类似于把微表面高度场拉大；

  • 类型：

    • Beckmann, GGX, etc.
    • Detailed models [Yan 2014, 2016, 2018, …]

    NDF01

b.2.1). Beckmann NDF

Beckmann NDF:

  • 和高斯函数相似

  • Project Solid angel上积分为1

  • 定义在Slope space（坡度空间）

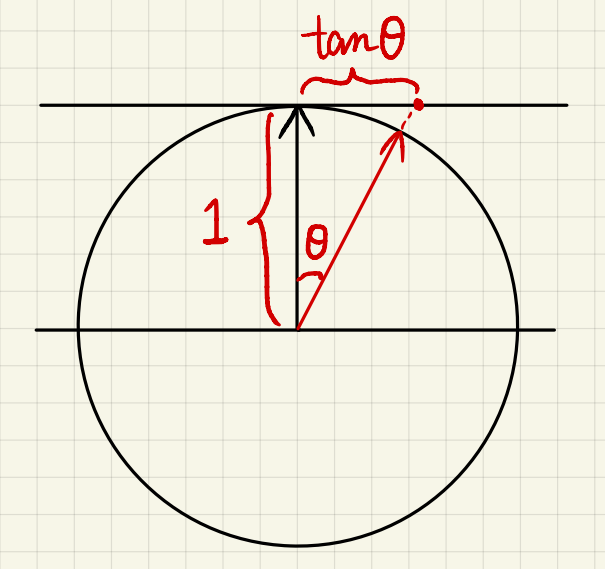
    NDF_Beckmann_01

    • 原因： 在Slope space（法线交点处切线平面）中Support无限大，任意位置对应的夹角不会超过90°，保证微表面不会朝下
  • $\alpha$ ：Roughness的平方
  • $\theta_{h}$ ：半角向量和（宏观）法线的夹角

b.2.2). GGX (or Trowbridge-Reitz, TR)

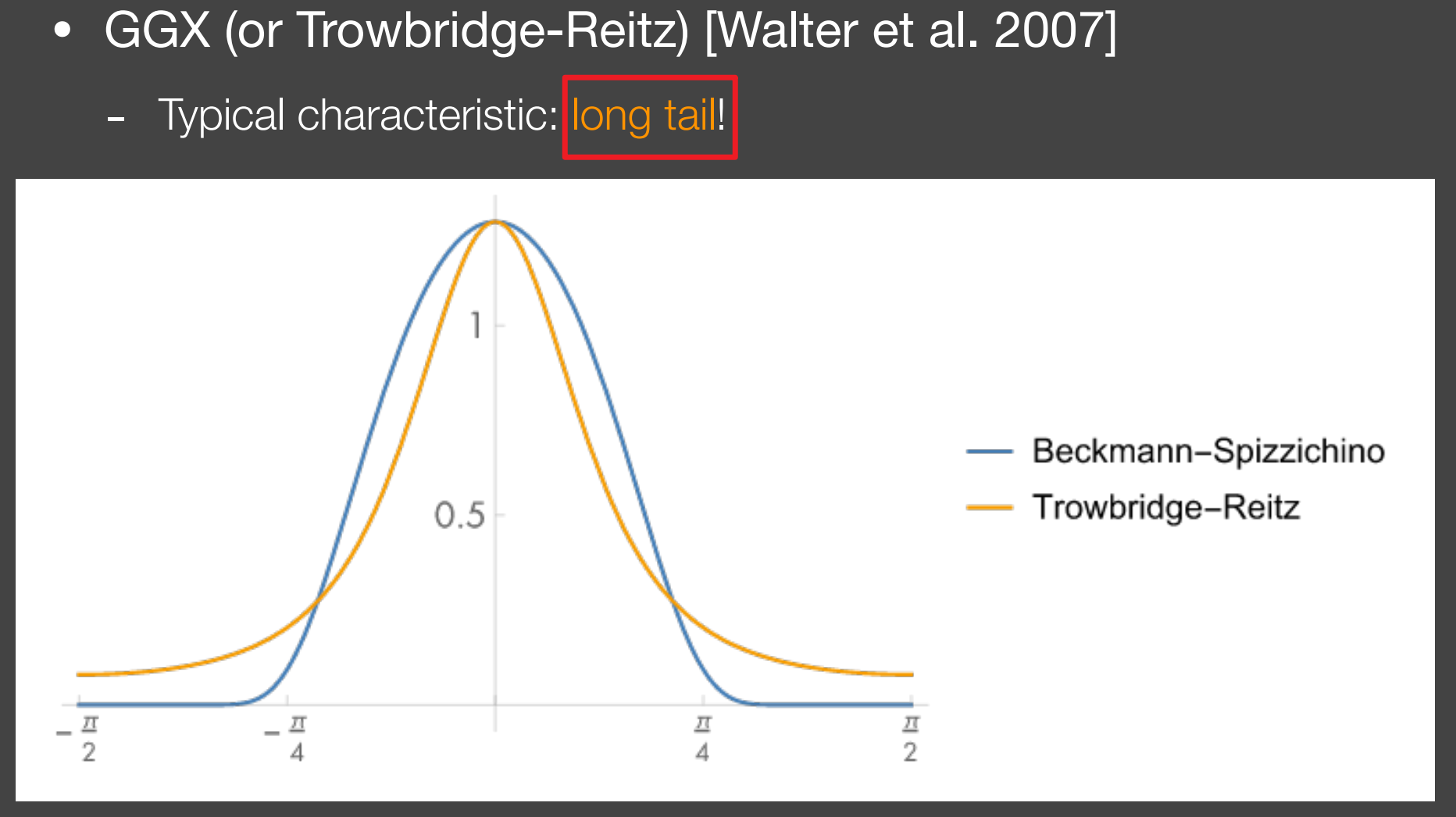
NDF_GGX01

  • Long tail: 使得光线过度更为自然，如高光过渡柔和

    NDF_GGX02

b.2.3). GGGX(GTR)

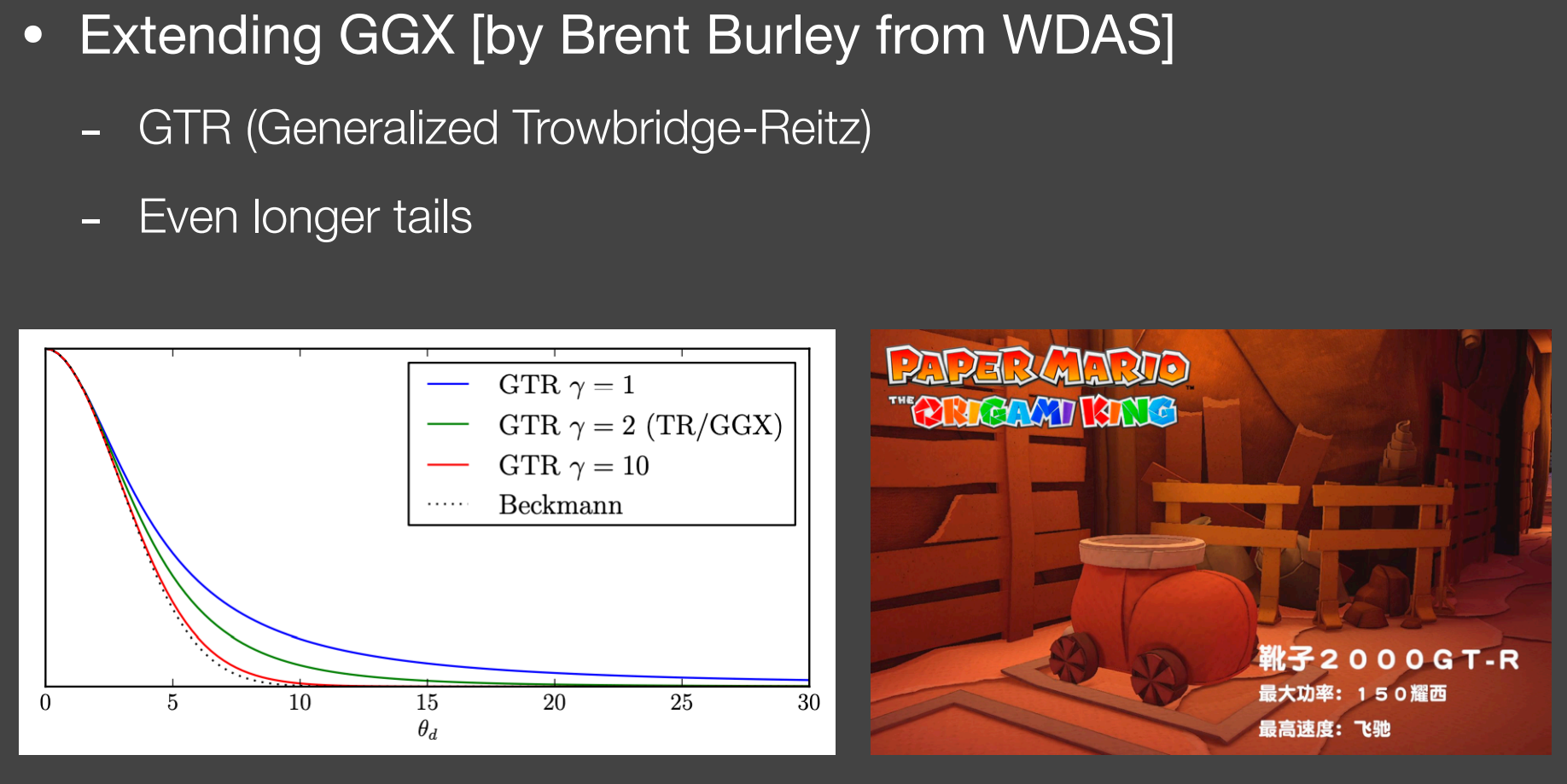
NDF_GTR

b.3). Shadowing-Masking Term

Why is it important?

  • 如没$G$ 项，在grazing angle时，物体表面会发亮；

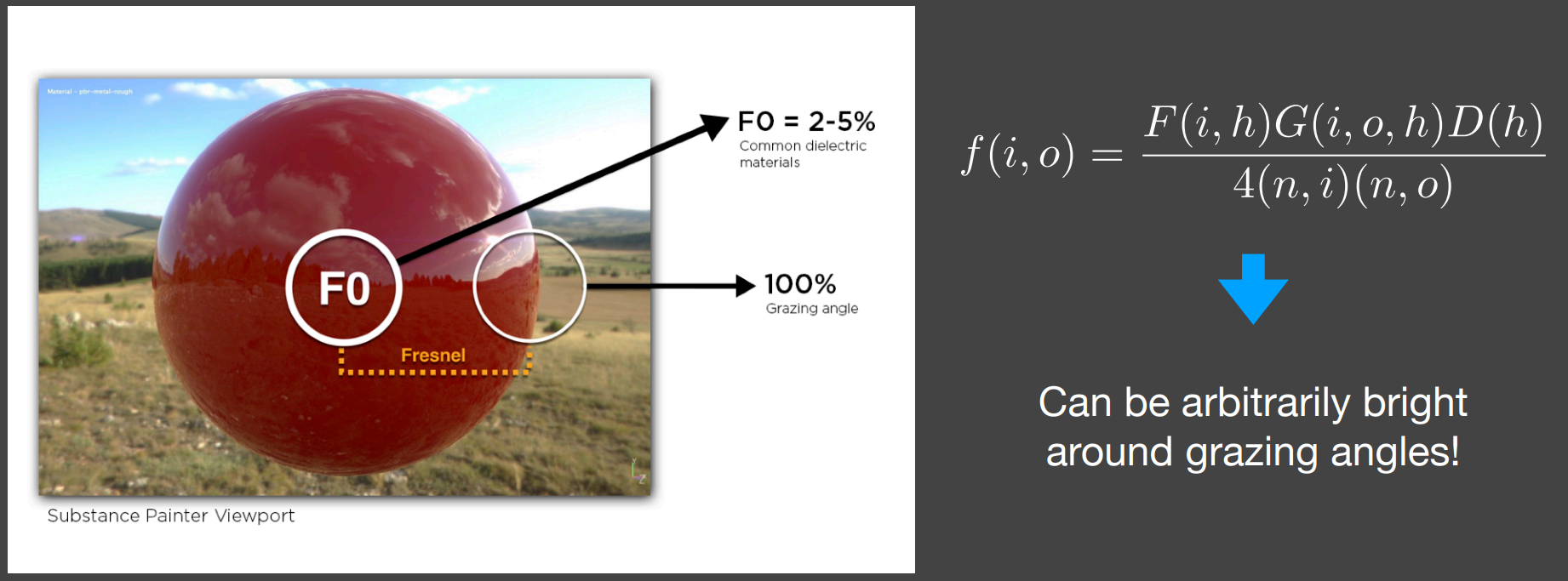
    MicrofacetBRDF_G01

b.3.1). The Smith shadowing-masking term

  • 假设： Shadow和Masking无关，即

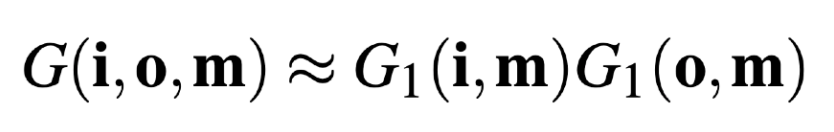
    Smith_01

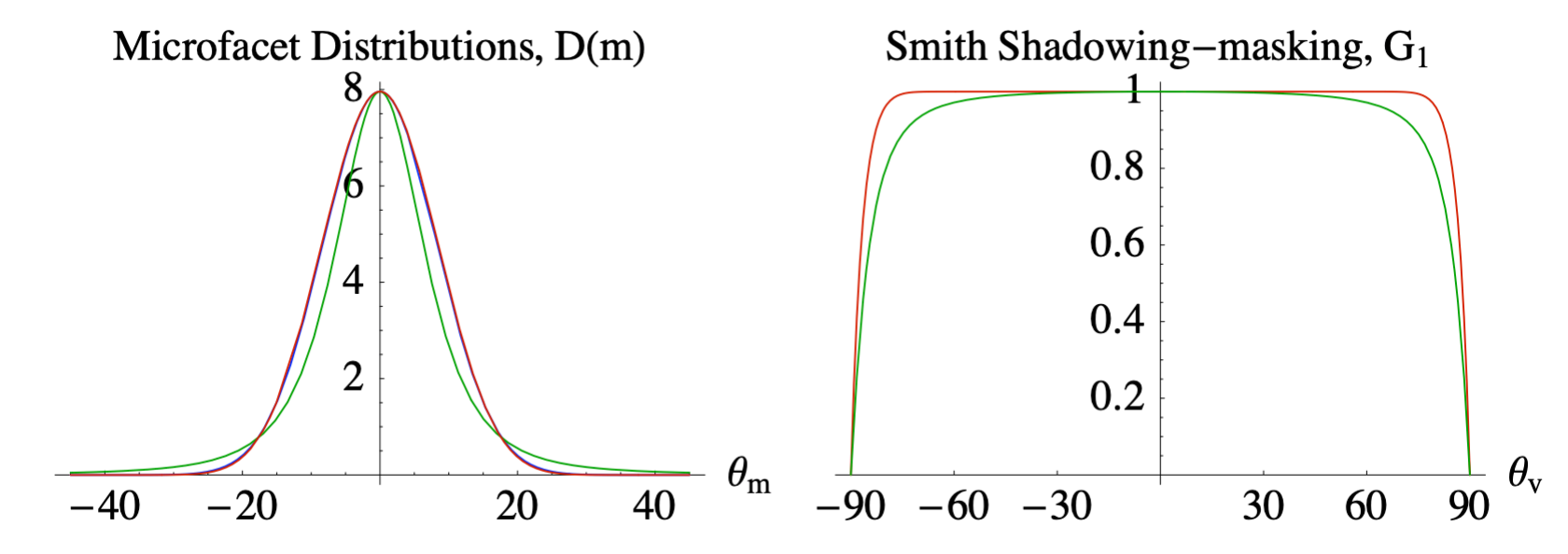
Smith_02

b.3.2). Issues(Missing energy)

  • 原因：由于Shadowing-masking只考虑了一次弹射，对于多次弹射的能量直接舍去，造成能量损失；

    WhiteFurnaceTest

ShadowMasking01

  • 做法：
    • Accurate methods exist [Heitz et al. 2016]
      • 主要用于离线渲染，对于RTR过慢；
    • The Kulla-Conty Approximation
      • Being occluded == next bounce happening
      • 构造函数去补偿损失的能量；
      • 求得的BRDF+原BRDF，即可；

b.3.3). Kulla-Conty Approximation

  • 通过对$\mathrm{d}\omega_{i}$ 换元（即立体角）

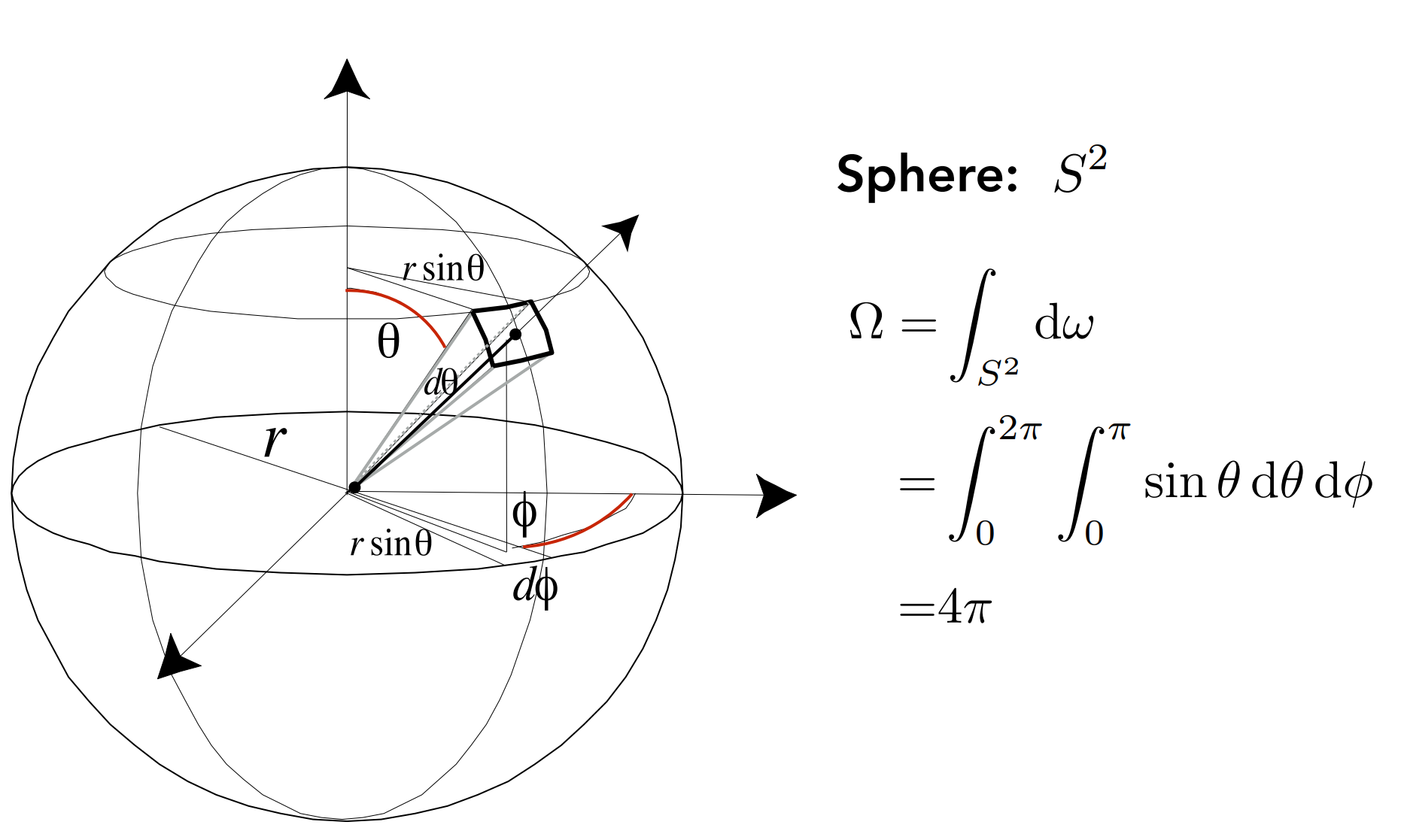
    SolidAngle_D02

    得到：

    Kulla-Conty

    • 此处假设各处入射Radiance（$L_i$） 均匀为1，因此出射的Radiance也应均匀为1；
    • 此处假设BRDF的菲涅尔项为1，即无颜色，能量不损失。后续再考虑颜色（？待验证）
    • 该函数是关于出射角的俯仰角$\theta_o$ 的函数（和方位角无关是因为假设为各项同性）

Key idea:

  • 通过积分可得需要补偿的能量为 $1 - E(\mu_{o})$；

  • 该函数是关于出射角的俯仰角$\theta_o$ 的函数（和方位角无关是因为假设为各项同性）

  • 考虑到对称性质（reciprocity），即入射方向和出射方向互换，Radiance不变，补偿项的BRDF形式为$c(1 - E(\mu_{i}))(1 - E(\mu_{o}))$，其中 $c$ 为常数；

补偿项的BRDF（带cos） - $c(1 - E(\mu_{i}))(1 - E(\mu_{o}))$

  • 常数 $c = \frac{1}{\pi(1-E_{avg})}, E_{avg}=2\int_0^1E(\mu)\mu\, \mathrm{d}\mu$

  • 补偿项即为：

    Kulla-Conty02

    • $c$ 推导：即让补偿项的BRDF$f_{ms}(\mu_{o},\mu_{i})$ 的积分结果为 $1 - E(\mu_{o})$

预计算

Kulla-Conty03

  • 对于$E_{avg}=2\int_0^1E(\mu)\mu\, \mathrm{d}\mu$ ，只需要得知其Roughness就可求出对应的结果，储存在1D table中；
    • NDF等使用的模型已知；
  • 对于$E(\mu)$ 得知其roughness(确定函数) 和 $\mu$ (确定函数自变量)，即可求出对应结果，储存在2D table中；

Kulla-Conty_Result

Result. 原BRDF+(uncolored)补偿项BRDF ↩

Color(energy loss)

  • 有颜色( vec3的$R_0$项 )，意味着能量被吸收，也是能量合理的损失；
  • 之前我们做了，不损失能量，无颜色的情况。之后，我们需要计算由于颜色的能量损失；

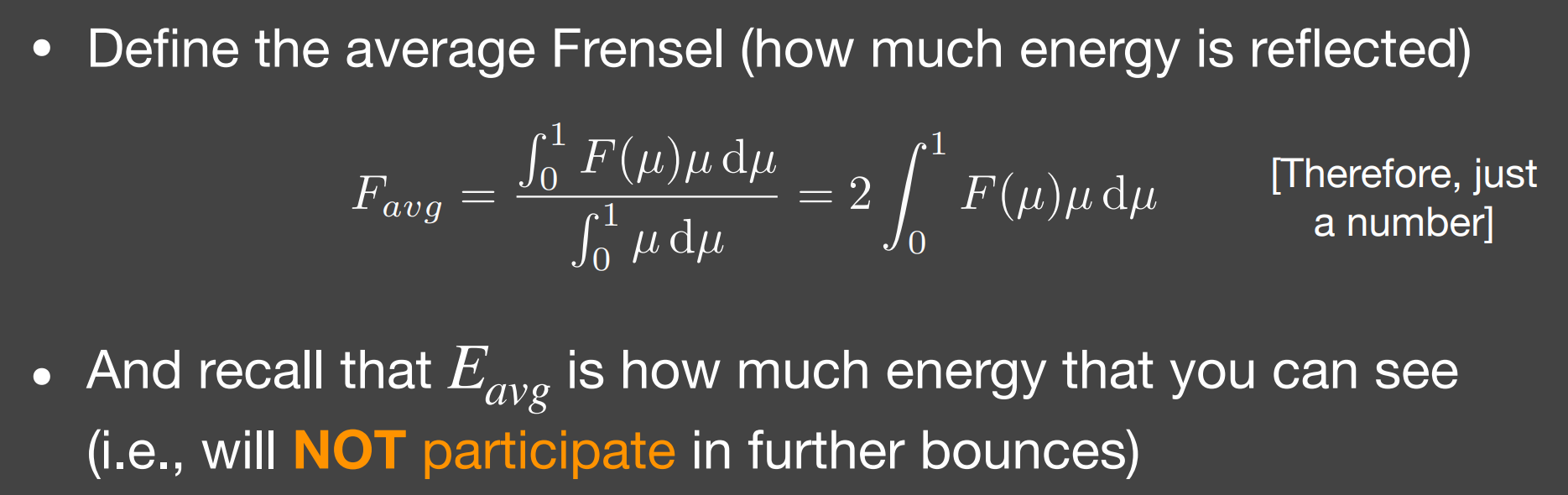
Kulla-Conty04

  • 定义平均菲涅尔 $F_{avg}$ ，表示能量参与弹射后，平均反射出多少；（剩下的被吸收）
  • 之前定义了 $E_{avg}$ ，表示每次弹射后，平均有多少能量被看见（即不参与之后的弹射）
  • $F_{avg}$ 、$E_{avg}$ 都是三维的向量；

  • 由此可得，

    Kulla-Conty05

    • $(1-E_{avg})$ 表示上一次弹射后，被遮挡未出射的能量；
    • 等比数列求和；
    • 求得的color term直接乘上uncolored additional BRDF即可；

    Kulla-Conty_Result02

    Result with color. 原BRDF + colored补偿项BRDF(color term * uncolor补偿项BRDF) ↩

c). Linearly Transformed Cosines(LTC, 线性变换余弦)

c.1). Introduction

作用： Solves the shading of microfacet models

  • 主要用于GGX，当然其他NDF也适用；
  • No shadows
  • Under polygon shaped lighting(多边形光源)，解决多边形光源的光照积分问题；

Key idea:

  • 对于任意一个球面分布函数，一定可以通过一个线性变换矩阵将其变化到另外一个球面分布函数(对于任意2D(二维，出射方位角和俯仰角) BRDF lobe can be transformed to a cosine)

  • 光源的形状也可以被变换，且积分结果相同；

  • 变换后的积分有解析解；

Ref:

[1] Real-Time Polygonal-Light Shading with Linearly Transformed Cosines

[2] Real-Time Polygonal-Light with LTC-zhihu

[3] 物理光源：Linearly Transformed Cosines

[4] Eric Heitz’s Research Page

[5] Global Illumination_Linearly Transformed Cosines (LTC)

[6] 图形学基础|基于LTC的面光源渲染

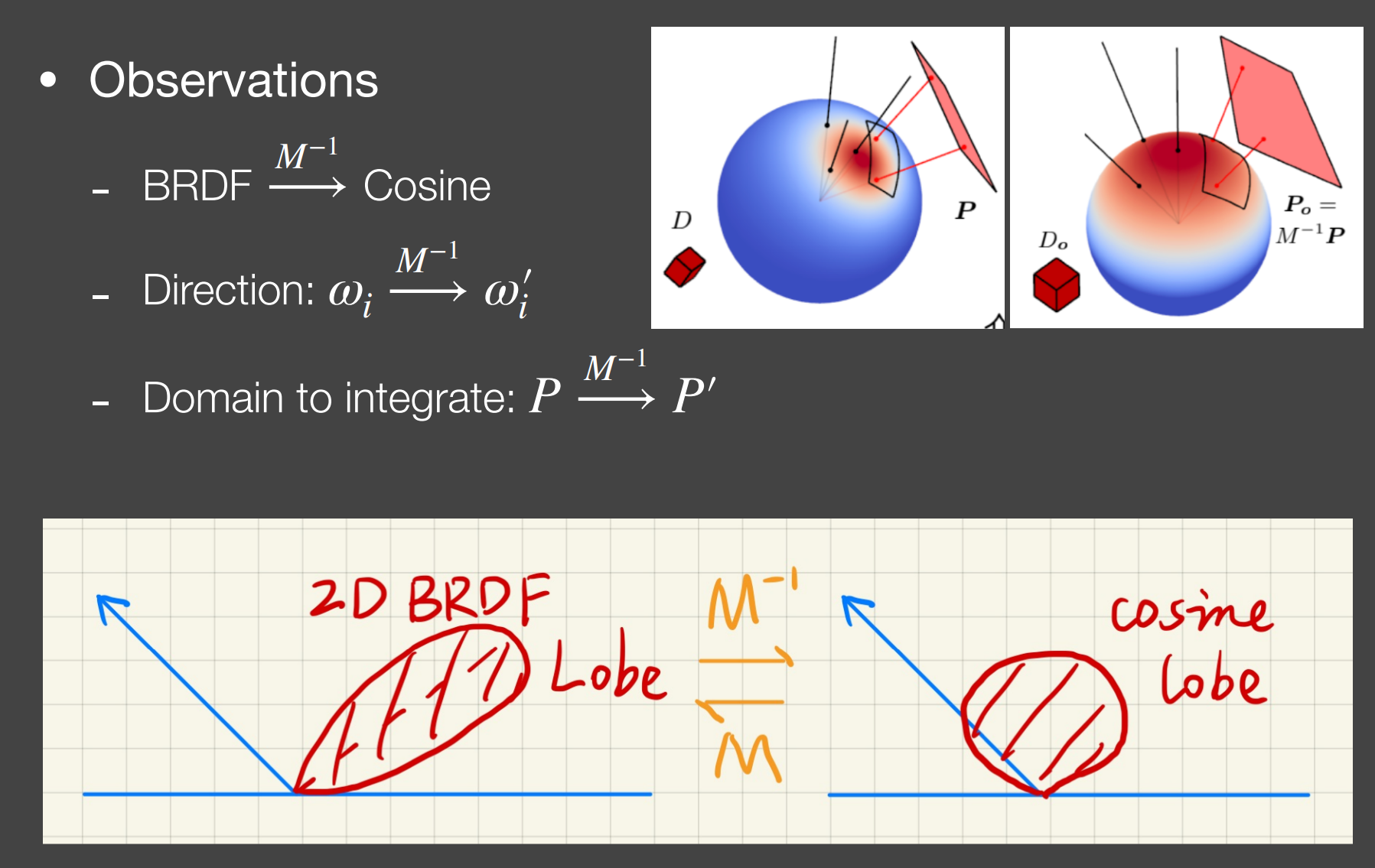
LTC01

LTC00

  • $J$ 是雅可比行列式，更进一步的可见Ref，后续论文复现后再进一步补充此处笔记；

LTC03

LTC介绍. 来源Ref[3] ↩

LTC04

LTC拟合BRDF. 来源Ref[6] ↩

d). Disney’s Principled BRDF

d.1). Introduction

微表面BRDF的缺点

  • 微表面模型不擅长表示真实（基于物理）的材质；
    • 如：Diffuse的情况不好表示，多层材质也难以表示；
  • 微表面模型“are not artist friendly”
    • 如： 复折射率（complex index of refraction）,$n-ik$（详见PBR-White-Paper）

需求：

  • Artist friendly，但一定程度上physically-based

设计原则：

  • 应该使用直观的而不是物理的参数；
  • 使用的参数尽可能少；
  • 参数应该在0~1；
  • 参数在必要时允许超出0~1的范围；
  • 参数的所有组合的外观都应该是合理、稳定的；

Disney00

Disney’s Principled BRDF. A table showing the effects of individual parameters ↩
  • sheen: 类似天鹅绒，材质表面有一层绒毛，使得其在grazing angle有雾化的效果
  • sheenTint: 绒毛的颜色
  • clearcoat: 类似清漆（当时做雨滴就用的是clearcoat）

d.2). Pros and Cons

  • 易于理解/控制
  • 可表现大量材质；
  • 实现复杂，基本是去拟合PBR材质；
  • 不基于物理，但视觉上大部分是符合的；
  • 参数空间巨大；