阴影总结（大纲）

发表于 更新于 分类于 ， 阅读次数：

image-20230819184600738

补充：

a). VSM

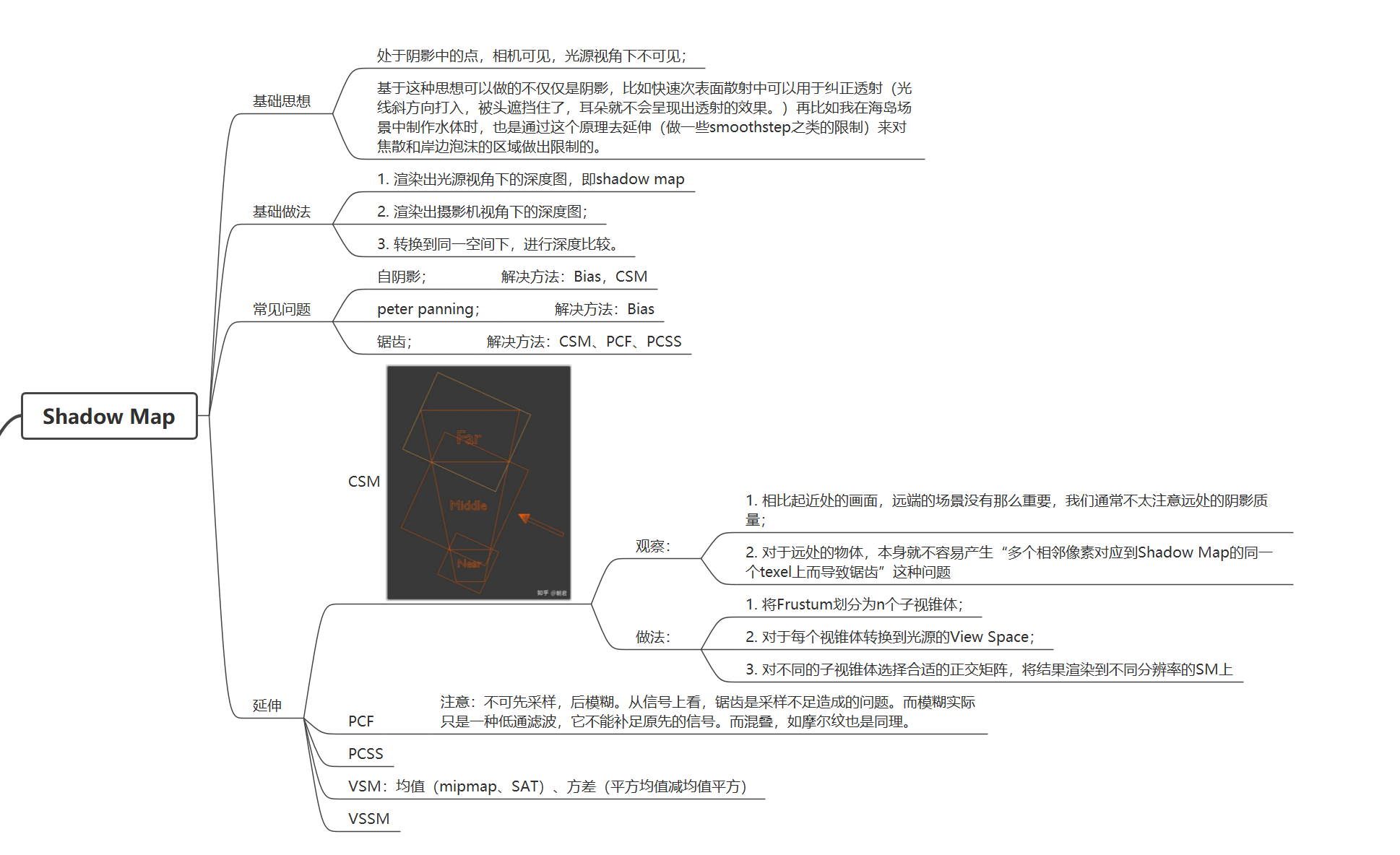
在PCSS第三步中，想要阴影越软，查询区域就越大，频繁的贴图采样可能造成IO瓶颈。因此，通过切比雪夫不等式求得PCSS第三步PCF中当前着色点深度在周围区域中的位置（深度小于当前着色点的比例）。

image-20231008151324301

b). VSSM

在求Average Block时，也应用切比雪夫不等式；

c). 切比雪夫不等式准确的条件

  • filter的平均深度大于着色点的深度（但大部分情况下不用管这个）；
  • 深度大致符合正态分布，不会有过于高频的变化（如多隔断的窗户就很可能造成阴影的不准确）；

d). ESM

image-20231008105537858

image-20231008105621660

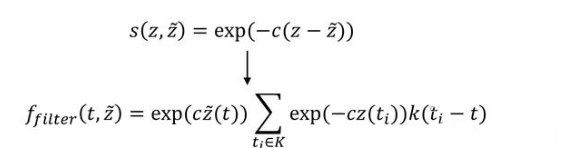
image-20231008105552336

  • 具体做法：

    1. 对Shadow Map应用指数形式进行预滤波（$e^{-cz}$ 处于0-1间）；
    2. 计算着色点的在Shadow map space 的深度，应用指数形式，得到 $e^{cd}$；
    3. $f(t,d)=saturate(e^{c*(d-z)})$；
  • 缺点：
    1. c越大，越准确，但随之也需要更高的精度去存储指数形式的深度值，一般需要32-bit的深度纹理。
    2. c小的时候有渗光的现象；
  • 优点：
    1. 漏光少，最终渲染时性能开销小（为k。PCF：计算阴影的时间复杂度是k*n，其中k是采样次数，n是片段数量），特别是在Overdraw严重的时候（对比非屏幕空间的PCF）；
    2. ESM对半透明、云影等表现好；

e). EVSM

VSM 中计算阴影值，考虑的是深度值的方差和均值，主要还是考虑深度的分布离散情况，如果将深度进行合理偏移，其仍符合切比雪夫不等式。

EVSM 里面采用了 $exp⁡(cz)$ 和 $−exp⁡(−cz)$ 两个函数进行偏移，然后取两个切比雪夫概率的较小值作为阴影值。（）

四张16bit纹理；

f). LVSM

分层；

g). Virtual Shadow Map

这个迟些写个专门讲解的文章，讲讲VSM、VT、RVT之类的（咕咕咕