Games202-3 Real-time Environment Mapping
Mesh Distance Fields,Real Shading in Unreal Engine 4
a). Shading from Environment Lighting(IBL)

- 通过环境贴图着色的方式,又被命名为 Image-Based Lighting (IBL)
a.1). How

- 对于IBL,可以看做是上半球(可以联想下UE中的HDRI)的光照和BRDF的积分;
Observation:
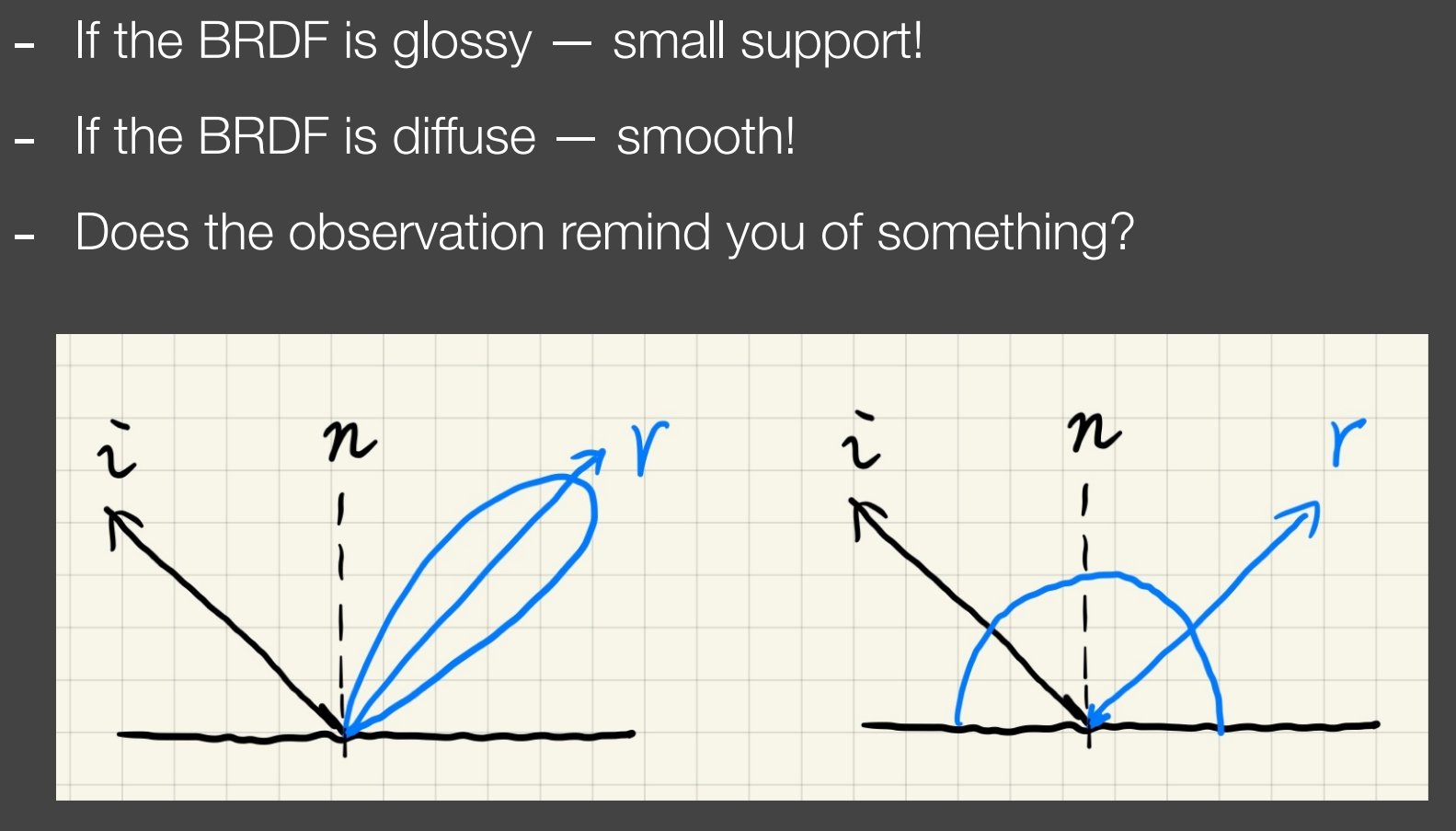
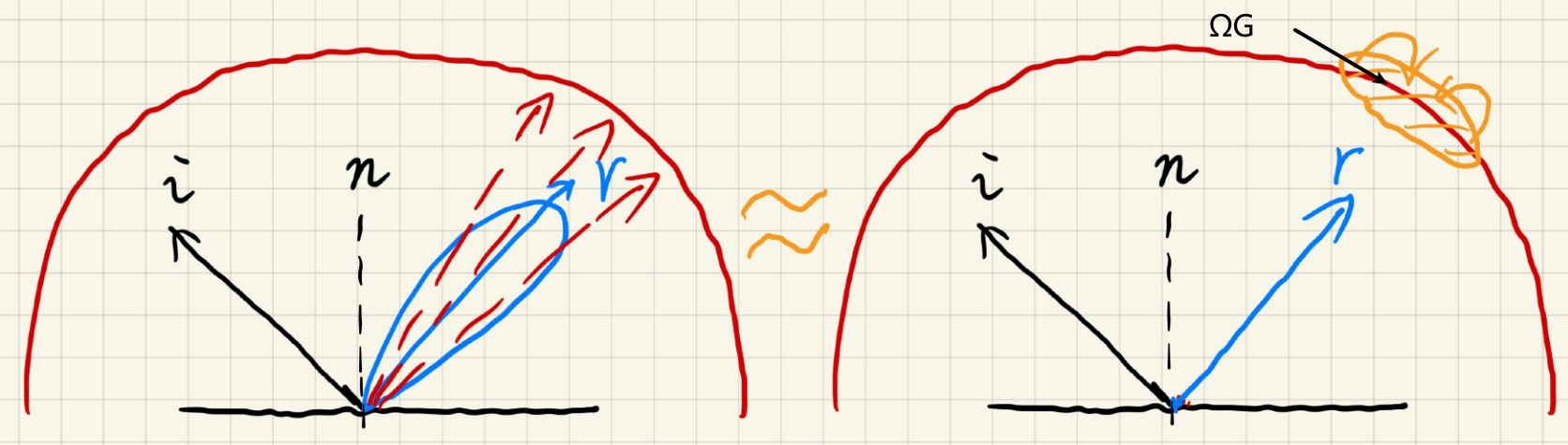
对于Glossy,其BRDF支持集很小(Lobe范围小);
对于Diffuse,其BRDF非常平滑;
联想到上节课渲染方程不等式成立的条件(拆出乘积积分的那个)
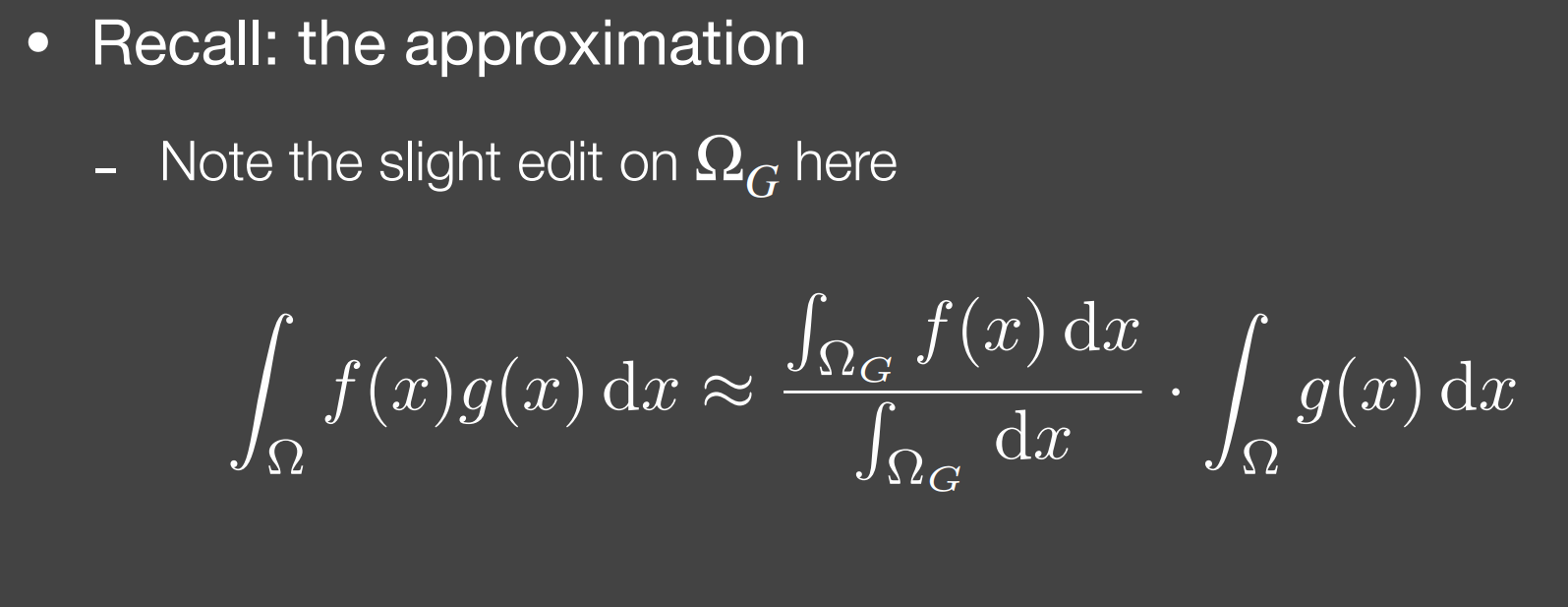
这里$\Omega_{G}$ 指积分域上,$g(x)$有值的区域。
如$g(x)$ 为BRDF,$\Omega_{G}$ 即为原点向Lobe各点出发,与积分半球相交的区域集合
We can safely take the lighting term out!

我们把渲染方程分为了两部分积分,分别是:
- 在$\Omega_{fr}$(即Lobe对应的半球区域),对光照Radiance积分
- 在半球内对BRDF积分;
Games202-2 Real-Time Shadow
a). Shadow Mapping
- A 2-Pass Algorithm
- Light pass: Generate the SM(Shadow Map)
- Camera pass: uses the SM
- An image-space algorithm
- Pro(优点): no knowledge of scene’s geometry is required
- Con(缺点): causing self occlusion(自遮挡) and aliasing(走样) issues
Pass 1: Render from Light
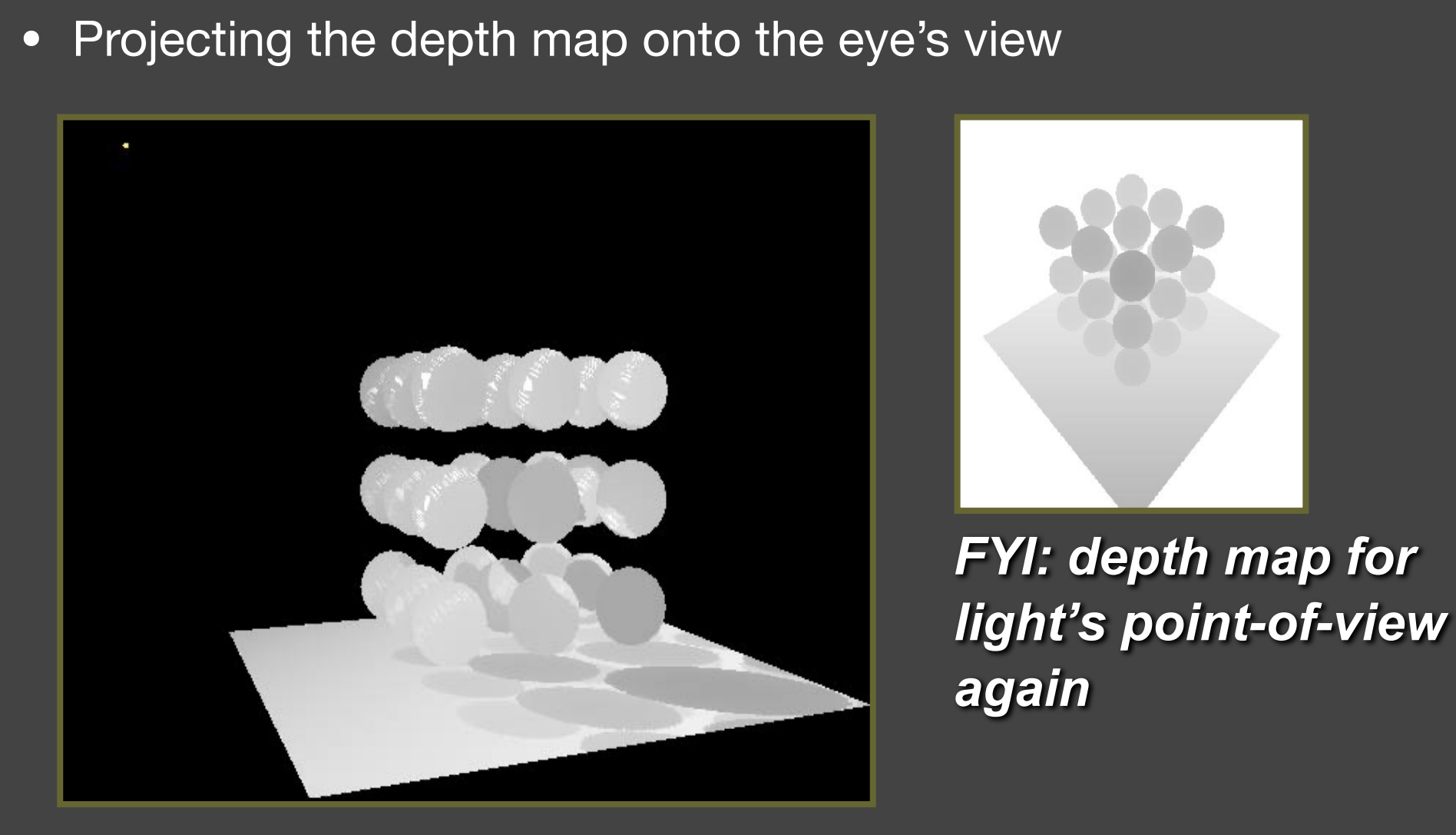
- 输出一张光源视角的深度图(Depth Buffer)
Pass 2: Render from Eye(Camera)
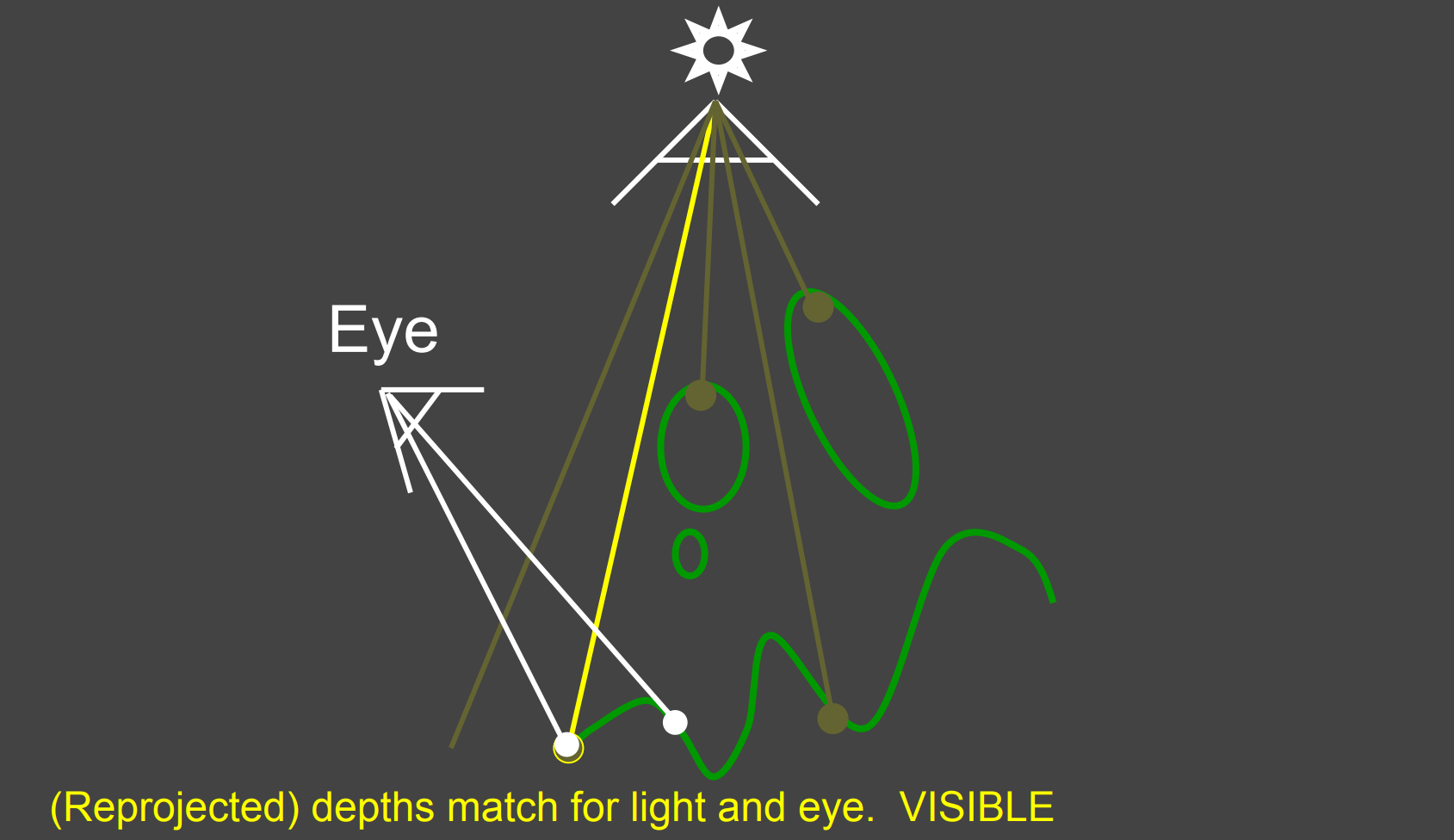
将光源视角对应的深度转换到View Space, 与Camera视角的深度进行深度比较;
- 如$Depth_{cam} > Depth_{light}$ ,那说明该点在阴影中(相机可见,光源不可见)
- 如$Depth_{cam} < Depth_{light}$ ,那说明该点在不在阴影中(相机可见,光源可见)
用于比较的深度值:
经过透视投影中的Squeez矩阵后(具体看Games101 Math笔记),z会被推向远平面
$M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right)$用于比较的$Depth$ 可以是经过MVP中的深度值(即Depth Buffer中的深度值);
- 也可以是该点在同一空间(如模型空间)中,该点到相机/光源的线性距离;
Games202-1 Recap of CG Basics
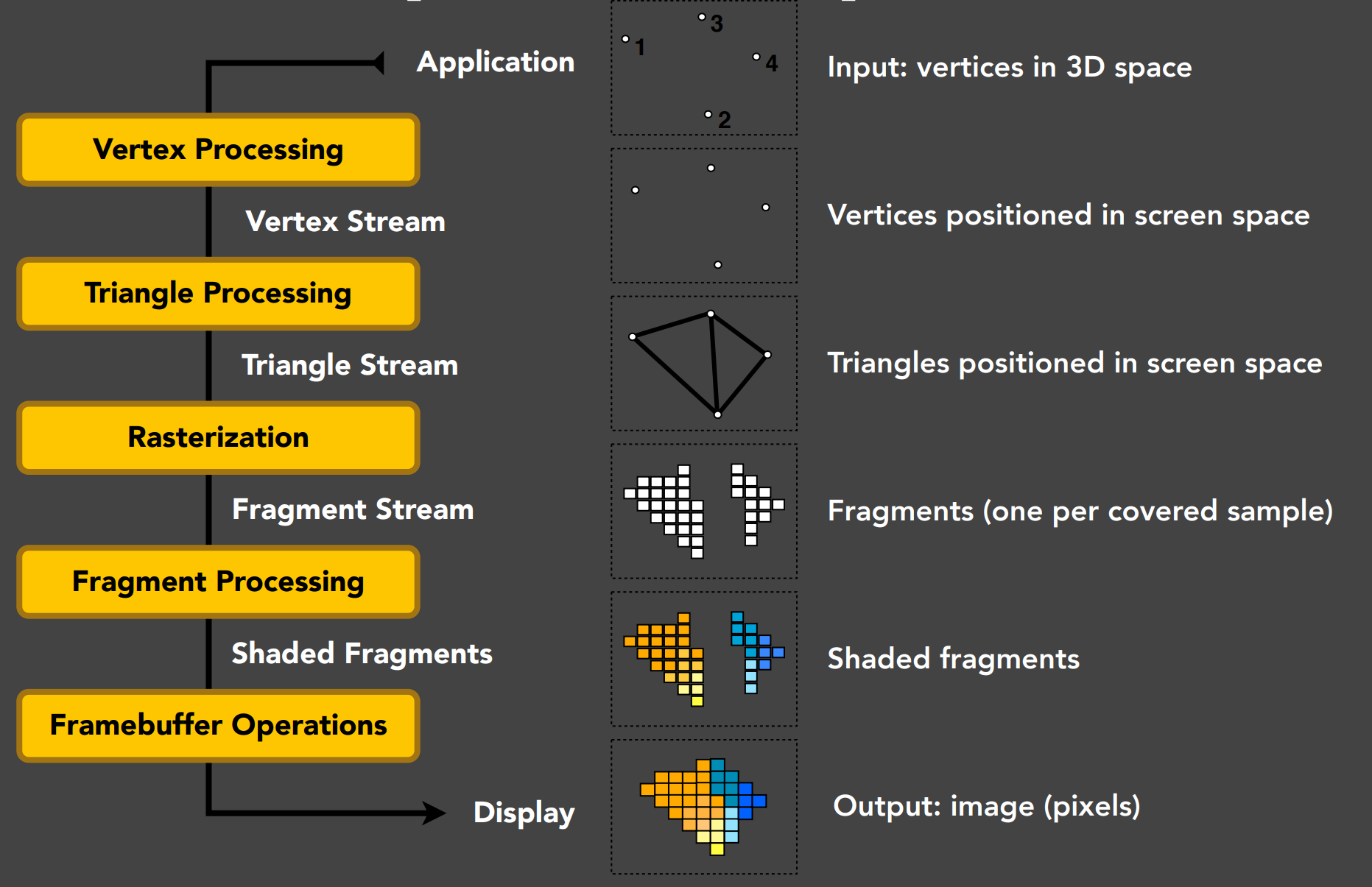
a). Graphics Pipeline
b). OpenGL

A. Place objects/models
- Model specification(模型信息)
- Model transformation

B. Set up an easel(画架)
- View transformation
- Create /use a framebuffer

C. Attach a canvas to the easel
指定Pass到framebuffer,就和Unity中FS的SV_TARGET一样。
E. you can also paint multiple pictures using the same easel
一个Rendering Pass,使用一个framebuffer,渲染一个或多个texture(shading, depth, etc.)作为输出
即一个framebuffer可以绑定多个纹理(MRT)
Multiple Render Target(MRT)是一种指可以使绘制程序在单帧中同时渲染多个Render Target
D. Paint to the canvas
- This is when vertex / fragment shaders will be used
- For each vertex in parallel
- OpenGL calls user-specified vertex shader: Transform vertex (ModelView, Projection), other ops
- For each primitive, OpenGL rasterizes
- Generates a fragment for each pixel the fragment covers
- For each fragment in parallel
- OpenGL calls user-specified fragment shader: Shading and lighting calculations
- OpenGL handles z-buffer depth test unless overwritten
Summary: in each pass
Specify objects, camera, MVP, etc.
Specify framebuffer and input/output textures
Specify vertex / fragment shaders
(When you have everything specified on the GPU) Render
Games101_19_20 Cameras Lenses and Light Fileds
Lecture19
讲相机的,老本行笔记直接看别人的吧;
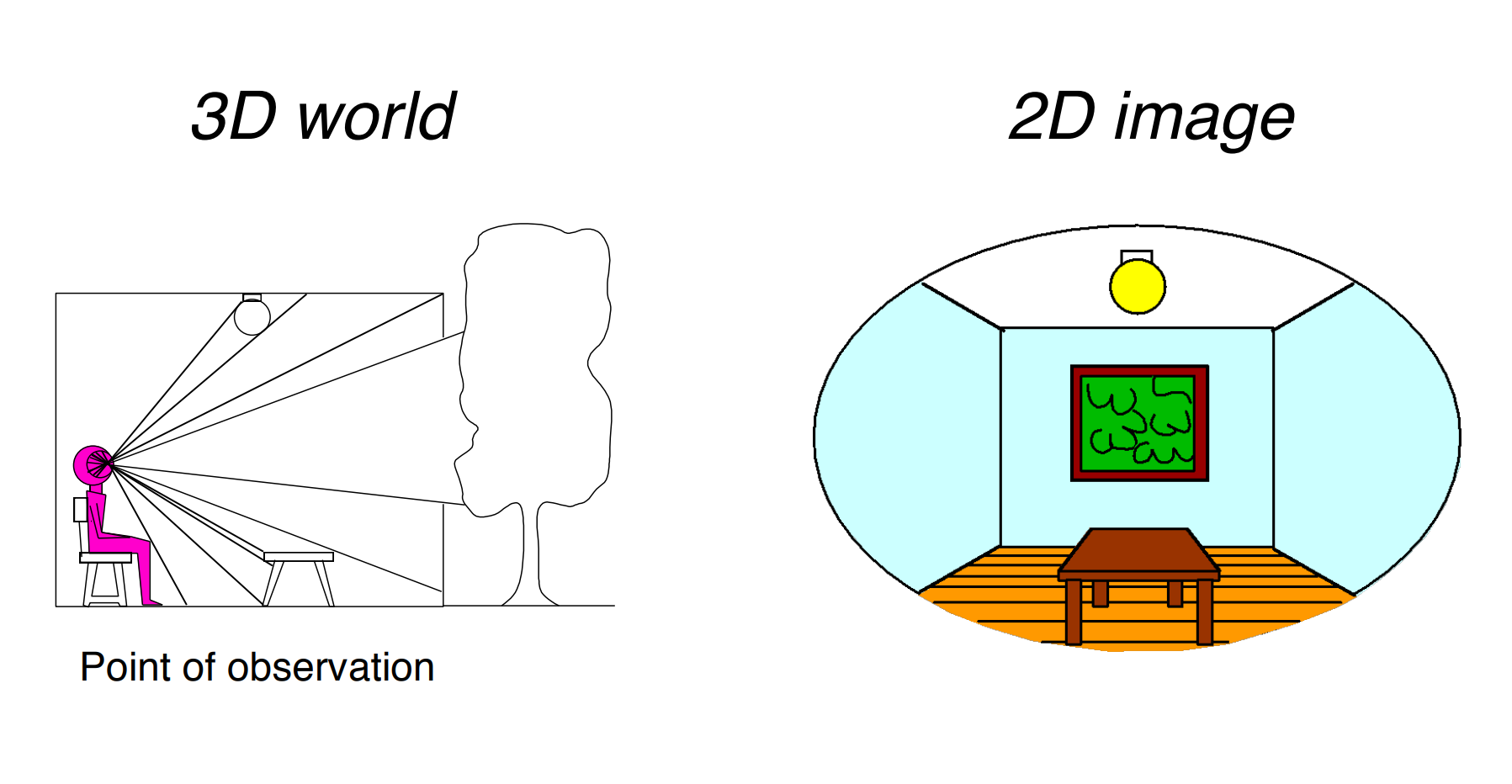
b). Light Field / Lumingraph(光场)
 |
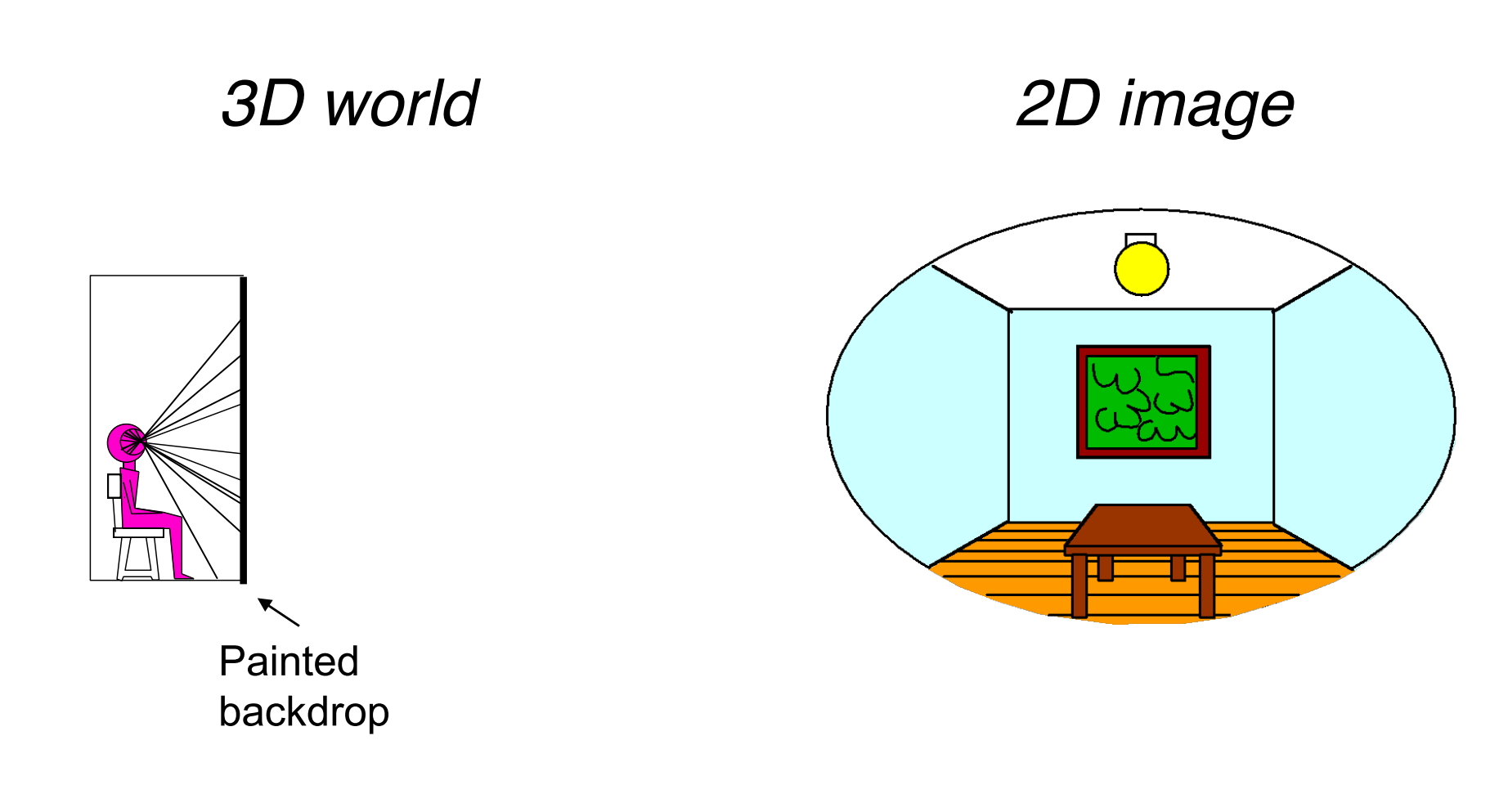 |
- 两者看到的光线信息完全相同,那人眼中的世界就完全相同;
b.1). The Plenoptic Function(全光函数)

- 现实世界可以用一个七维的全光函数进行描述,记录了任意时间,不同位置的不同方向接收光的波长
- 参数:
- $\theta$ :方位角
- $\phi$:俯仰角
- $\lambda$:波长
- $t$:时间
- $V_X,V_Y,V_Z$:位置
b.2). Light Field
光场则可以认为是记录了任何一个点所接收的任何一个方向的irradiance。
- 可用四维函数表示,二维描述位置,二维描述方向
- 光线可由两个点定义,因此这四维可改写成s,t,u,v。即两个平面上的位置;
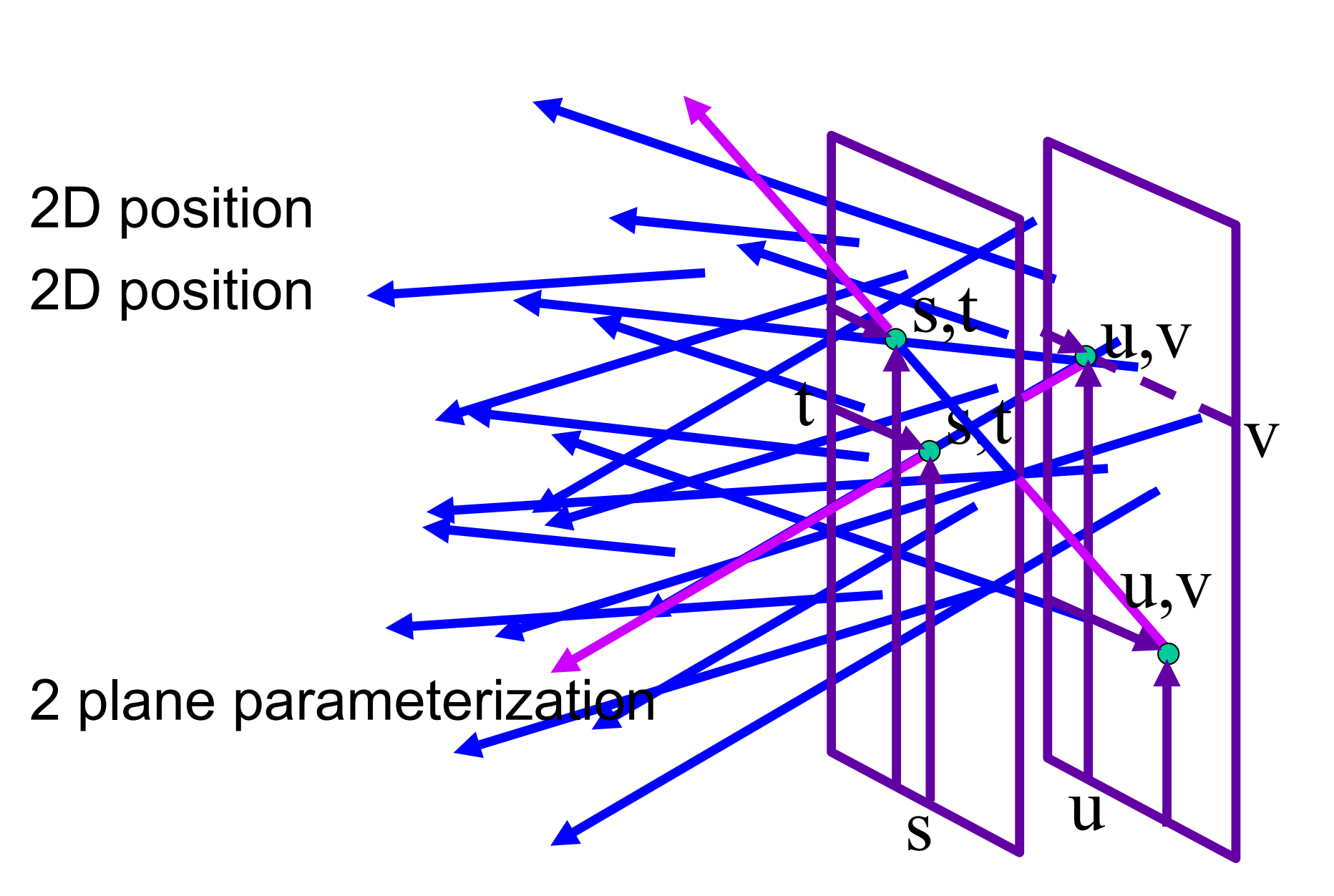
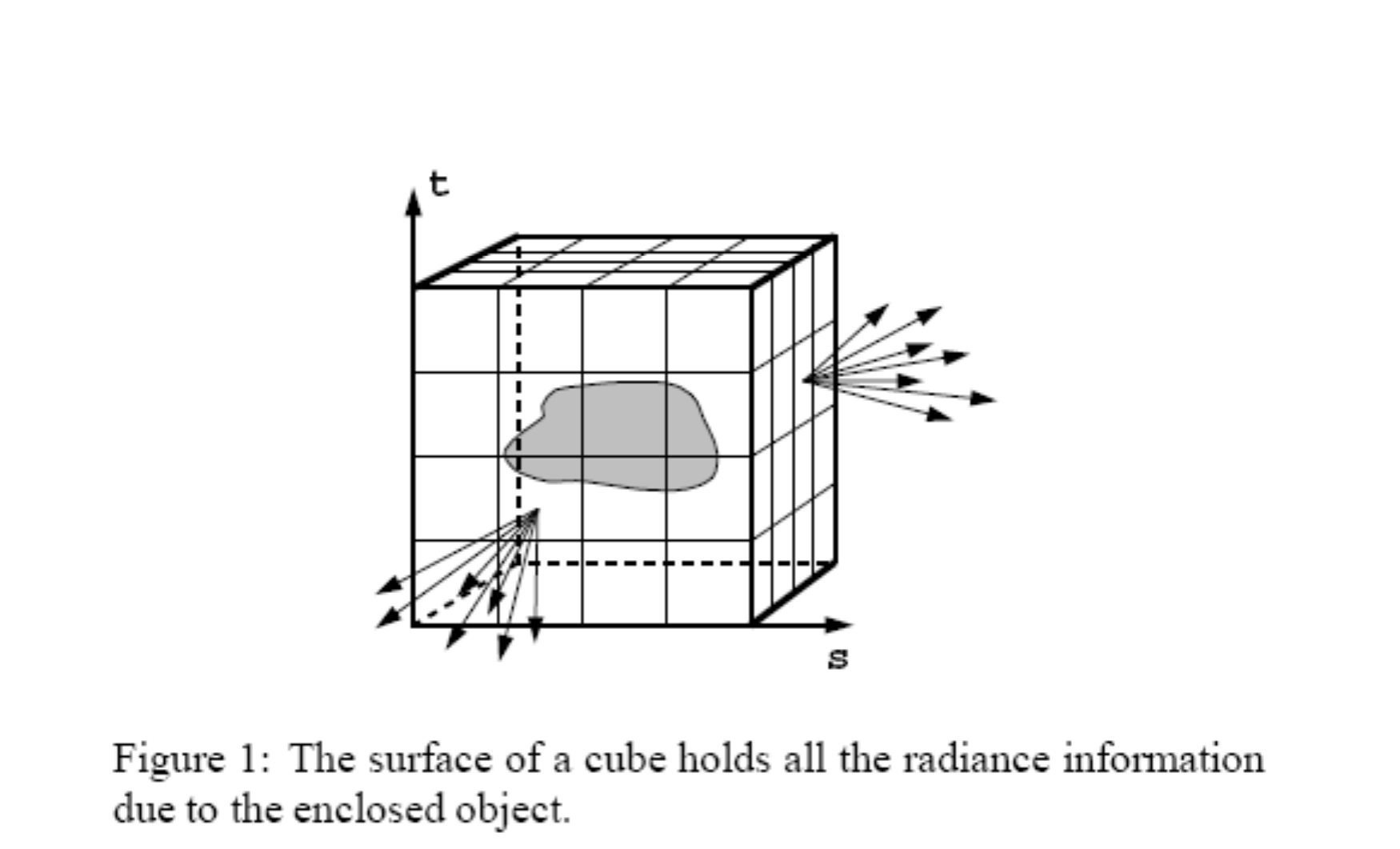
由此得出,描述一个物体的光场,只需要记录其包围盒上四维的全光函数即可
从uv平面看向st平面,得到的是这个物体从各个方向看的相应的图像;
而从st看向uv,则得到的是这个物体在这个方向的irradiance的集合(不是合起来,而是类似二维数组的集合)即radiance
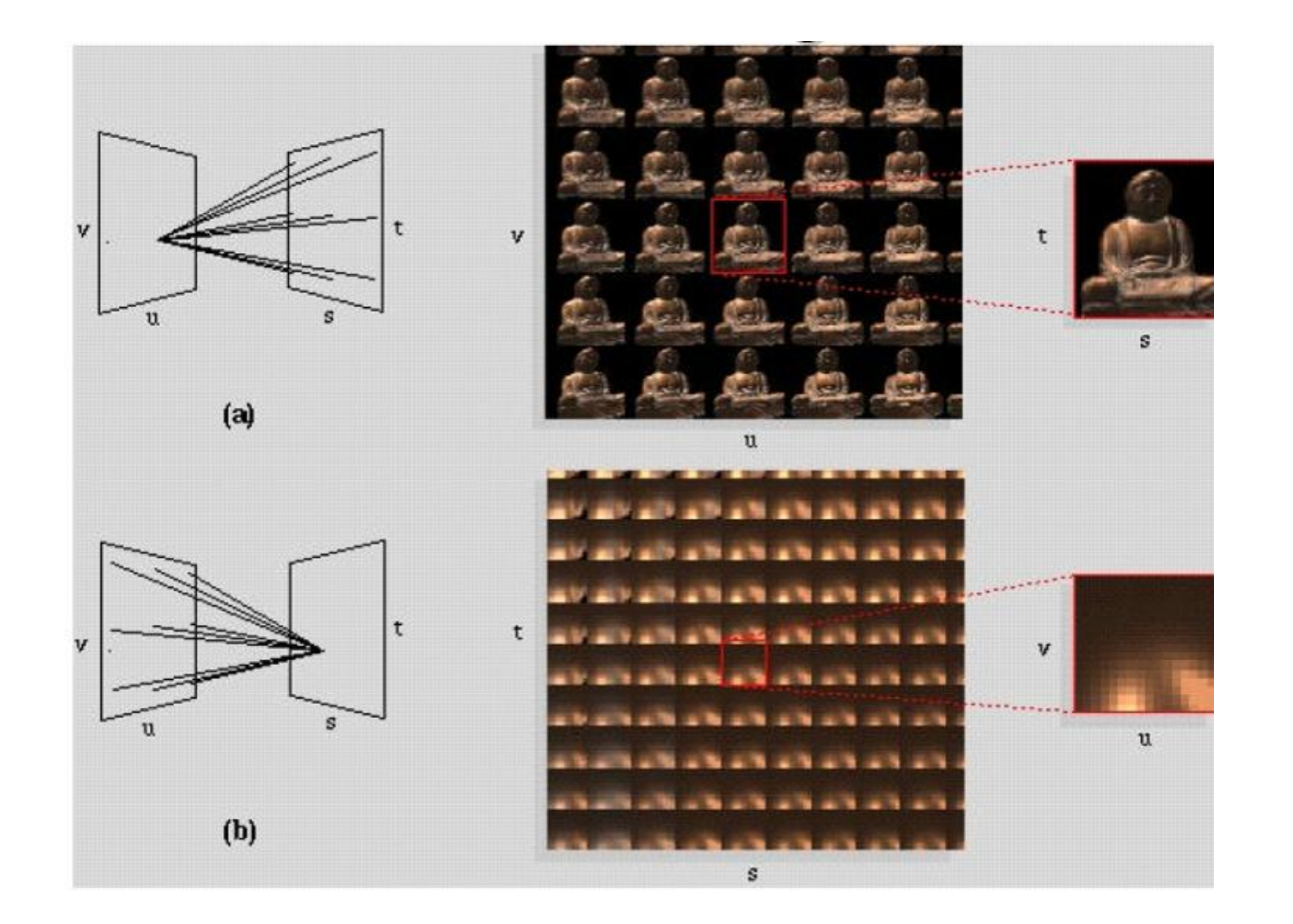
st到uv
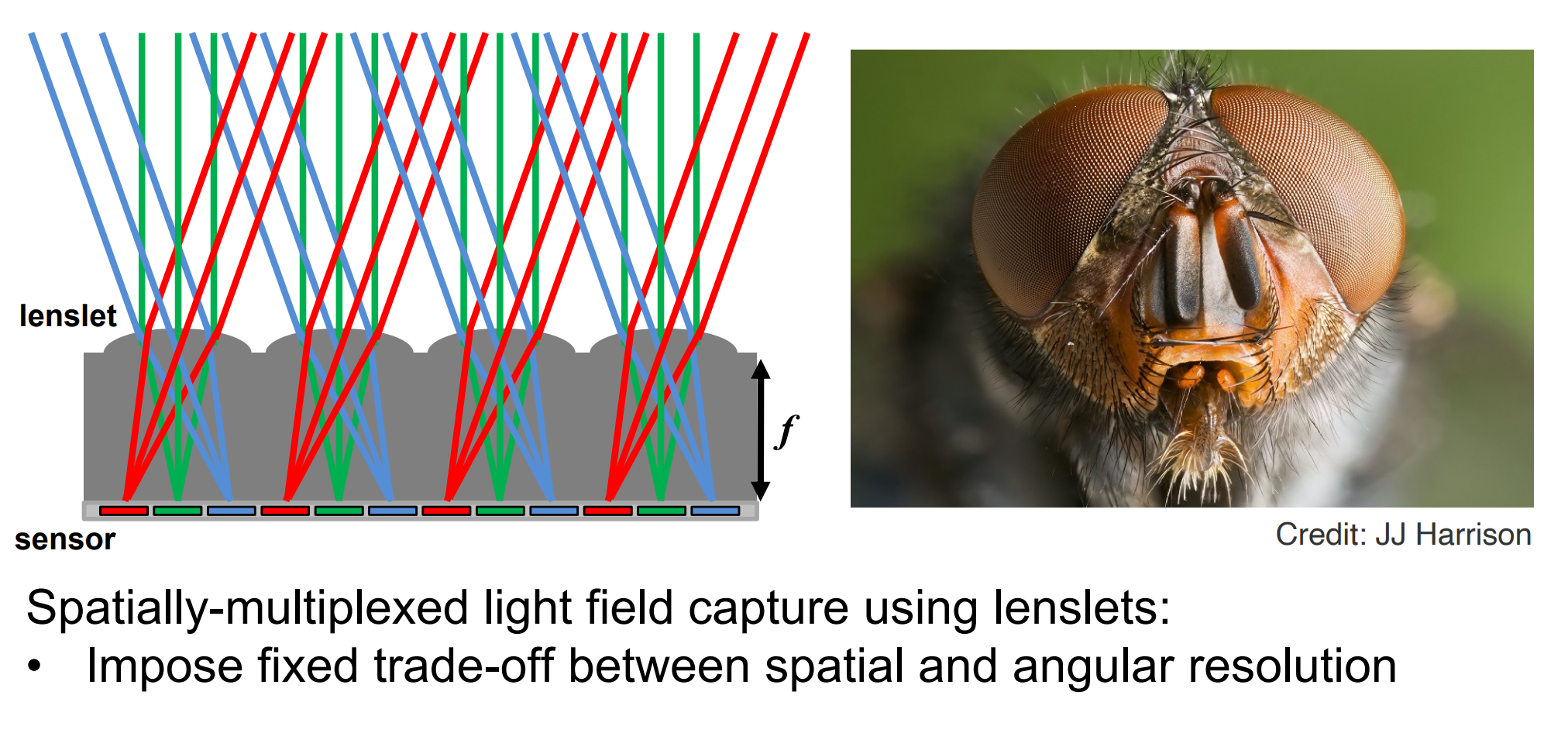
- 记录不同方向的光线radiance(注意和拜耳阵列的区分,这里三色只是代表不同方向)
Games101_17_18 Materials
Lecture 17 Materials and Appearances
Material == BRDF
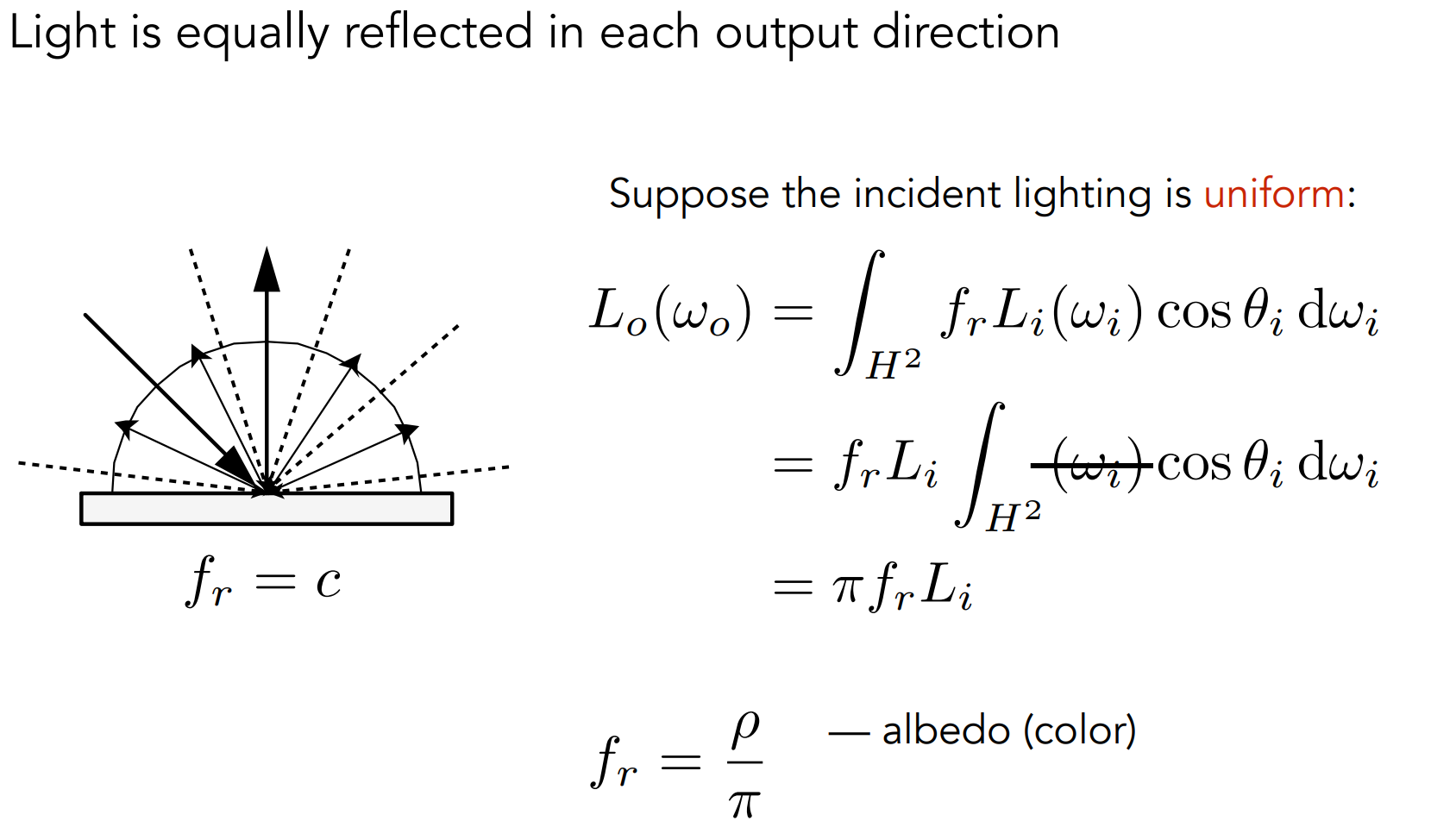
a). Diffuse / Lambertian Material
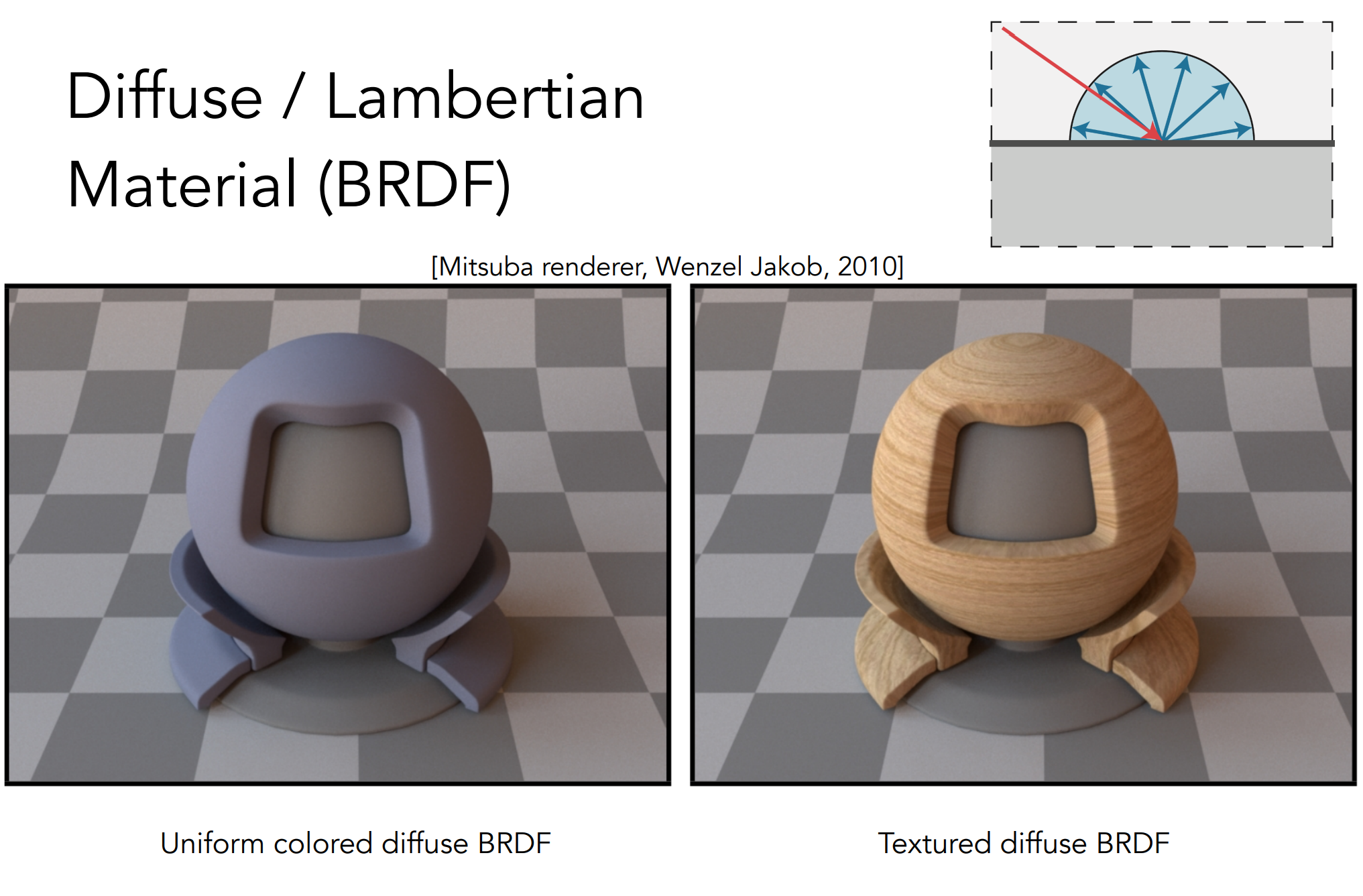
对于此类材质,当假定各方向9入射的光线radiance相同,反射的光同样是Uniform的。因为能量守恒(假定不发光,不吸收),使得进入的 Irradiance入 和出去的 Irradiance出 相同;
b). Glossy material

c). Ideal reflective / refractive material(BSDF)

计算镜面反射方向
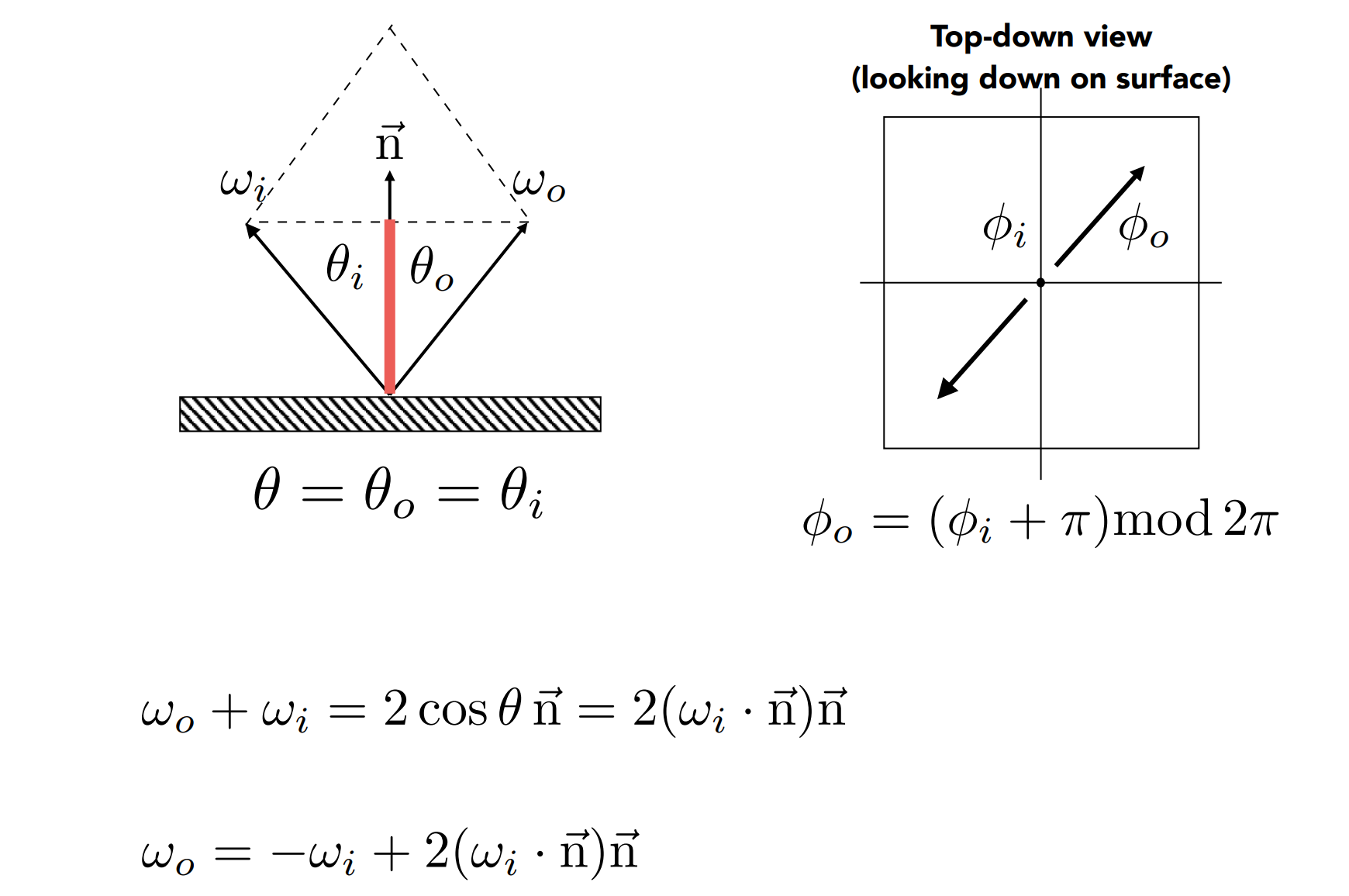
- 几何
- 方位角
c.1). Specular Refraction

现象:色散、Caustic等
Snell’s Law
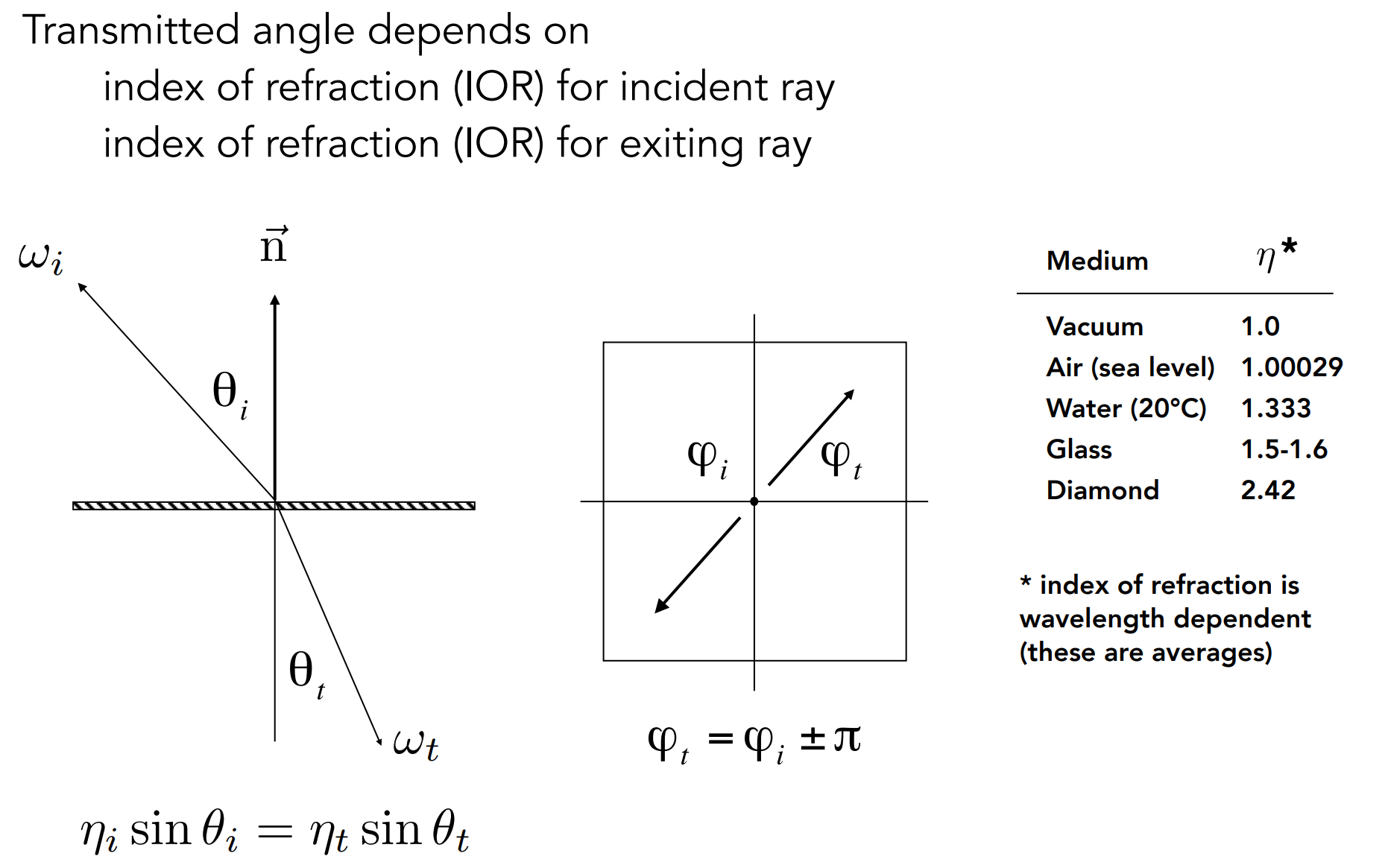
可推出只有当光密到光疏介质时,才有可能发生折射;(${n_i\over n_t}>1$)
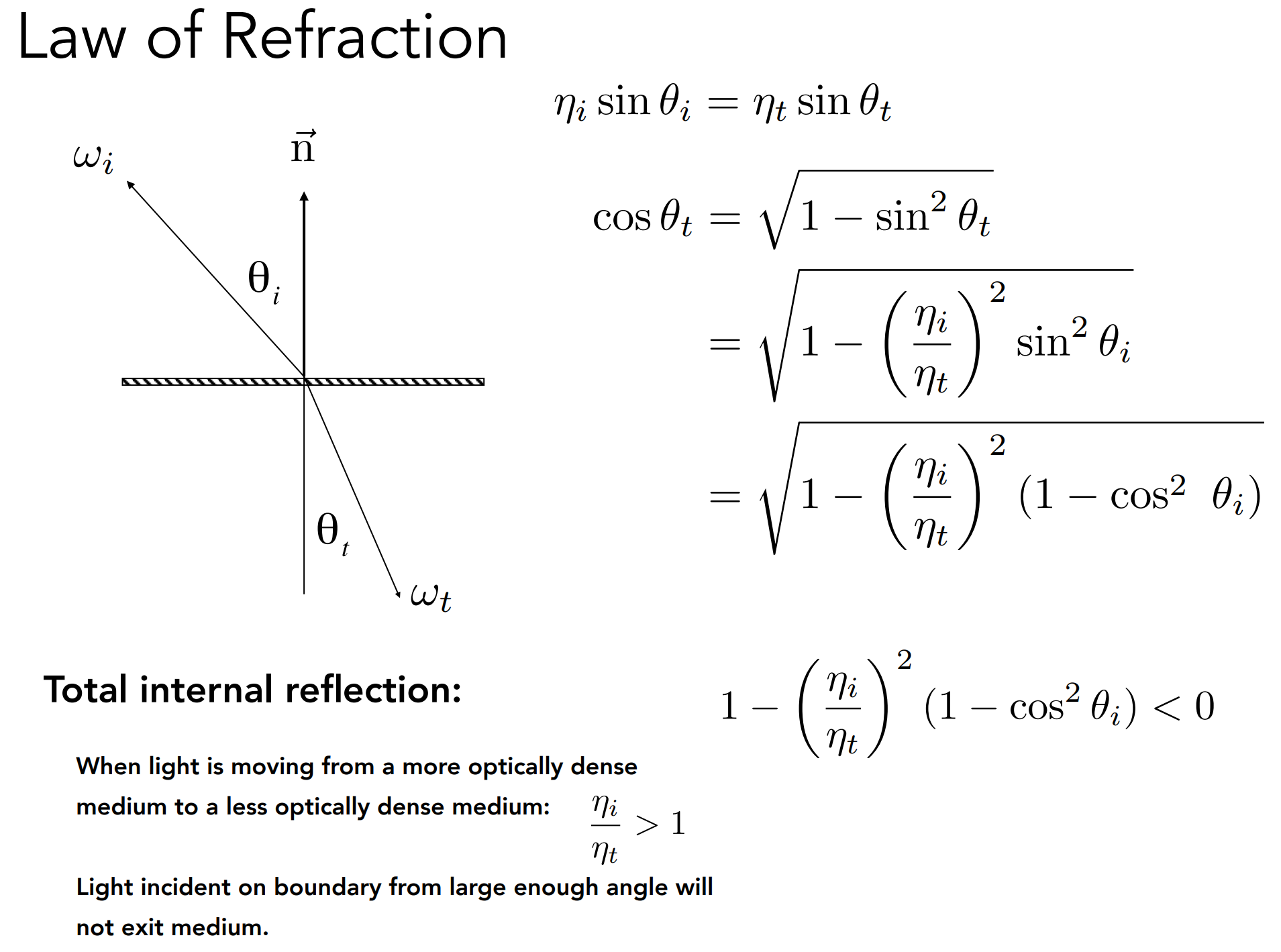
折射属于BT(Transmit)DF;
- BTDF + BRDF = BSDF
c.2). Fresnel Reflection(菲涅尔)
- 反应了特定方向的入射光的反射和折射的比例;
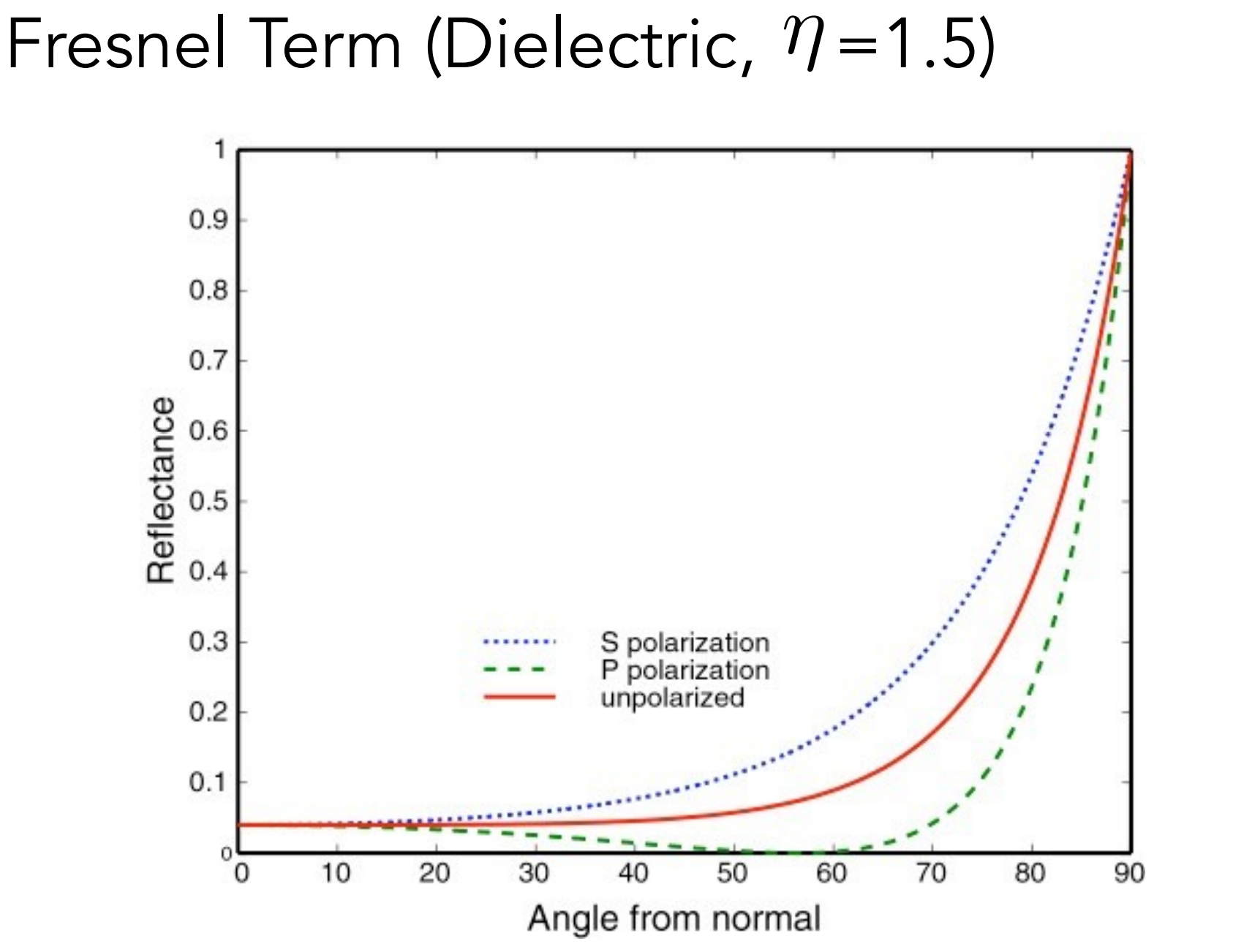 |
_Fresnel.png) |
- 左图是绝缘体的菲涅尔项,右图是导体(金属)的菲涅尔项

Games101_21_22 Animation
Lecture 21 Animation
a). History
b). Keyframe
c). Physical Simualtion

c.1). Mass Spring System
Idealized spring
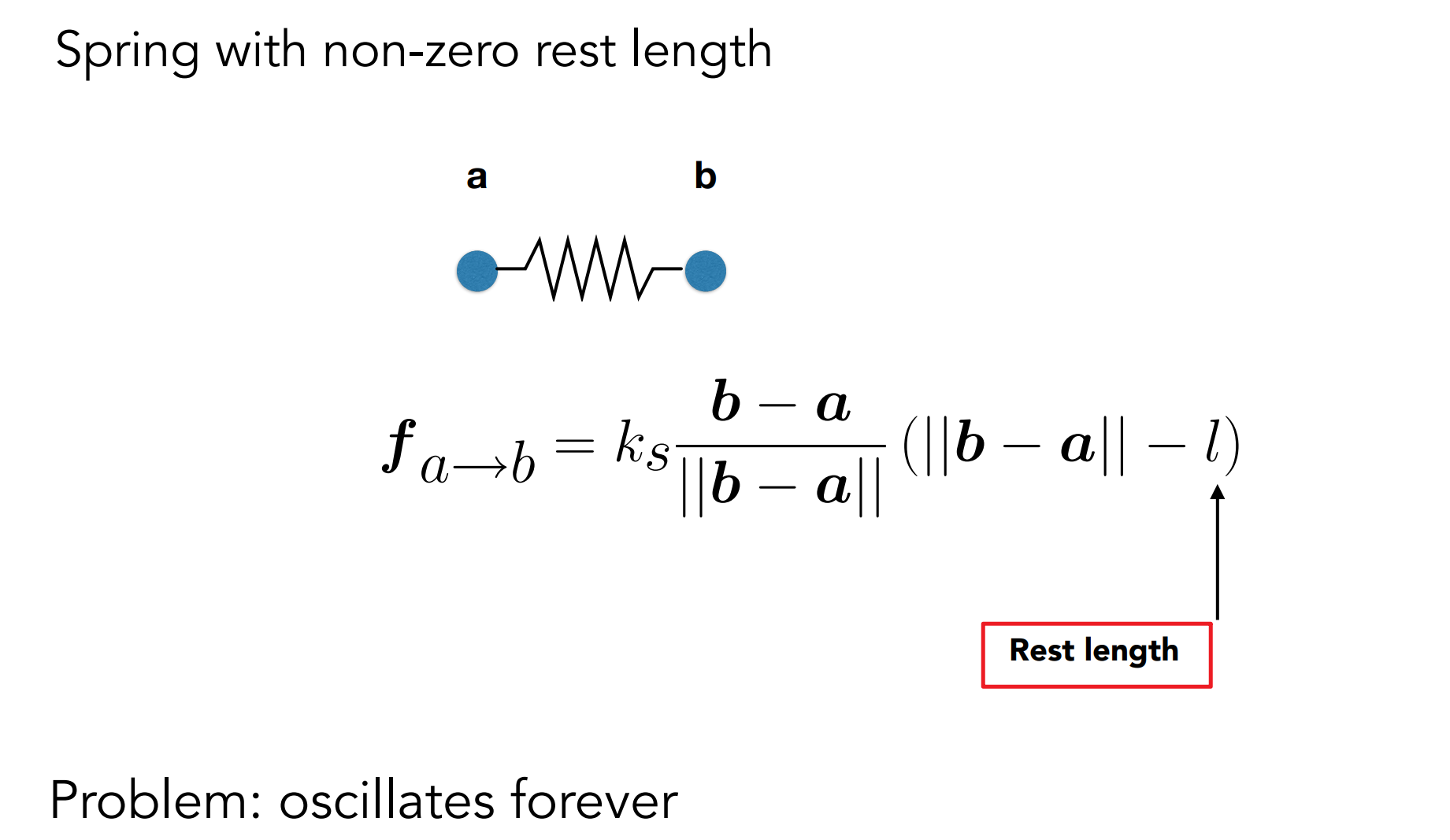
- 但永远不会停止,因此加入摩擦力
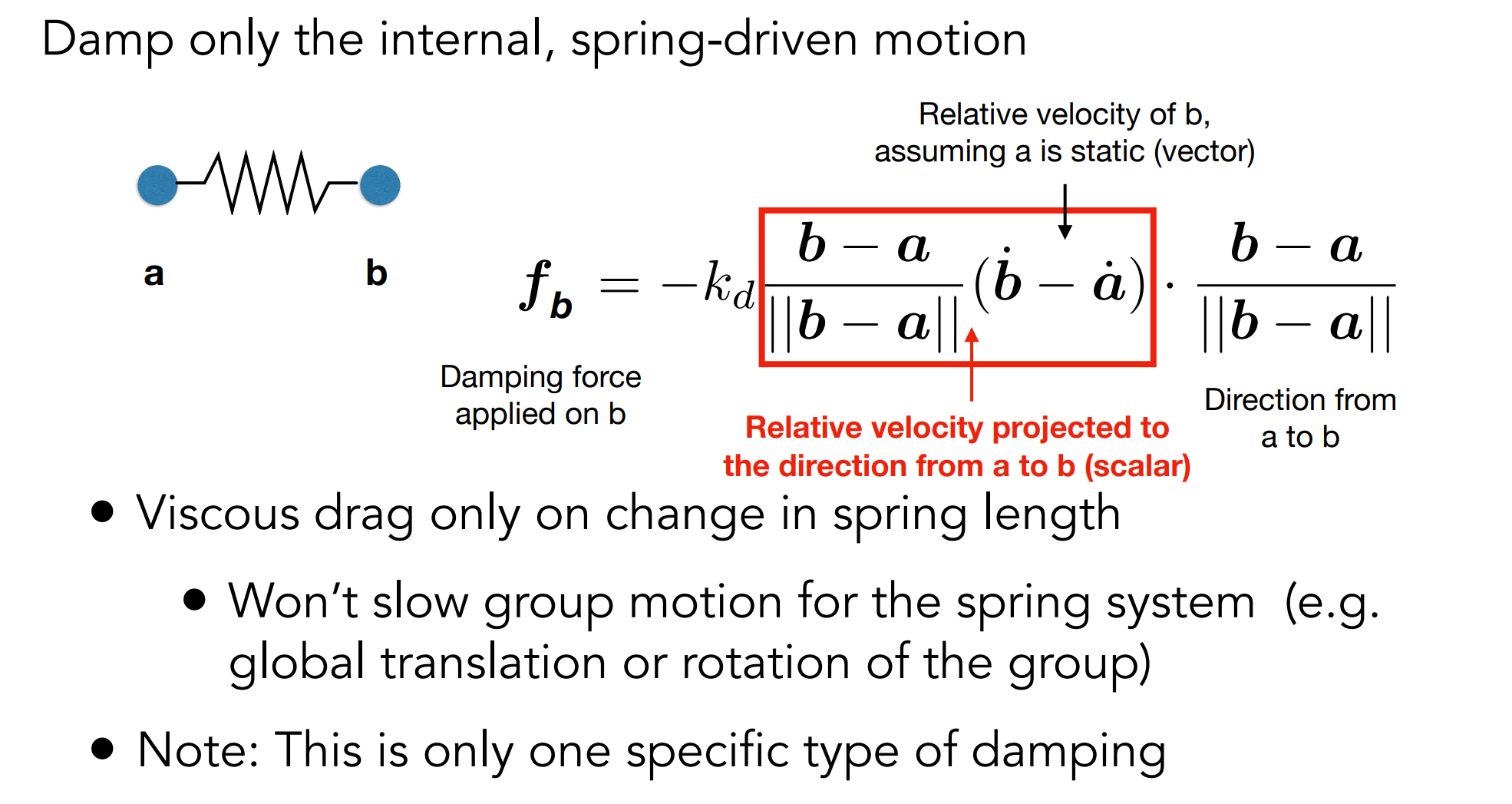
中间项为相对速度在向量$ab$方向的投影,因为(处于原长状态时)如果a点不动,b点绕a点做圆周运动,那$f_b=0$;
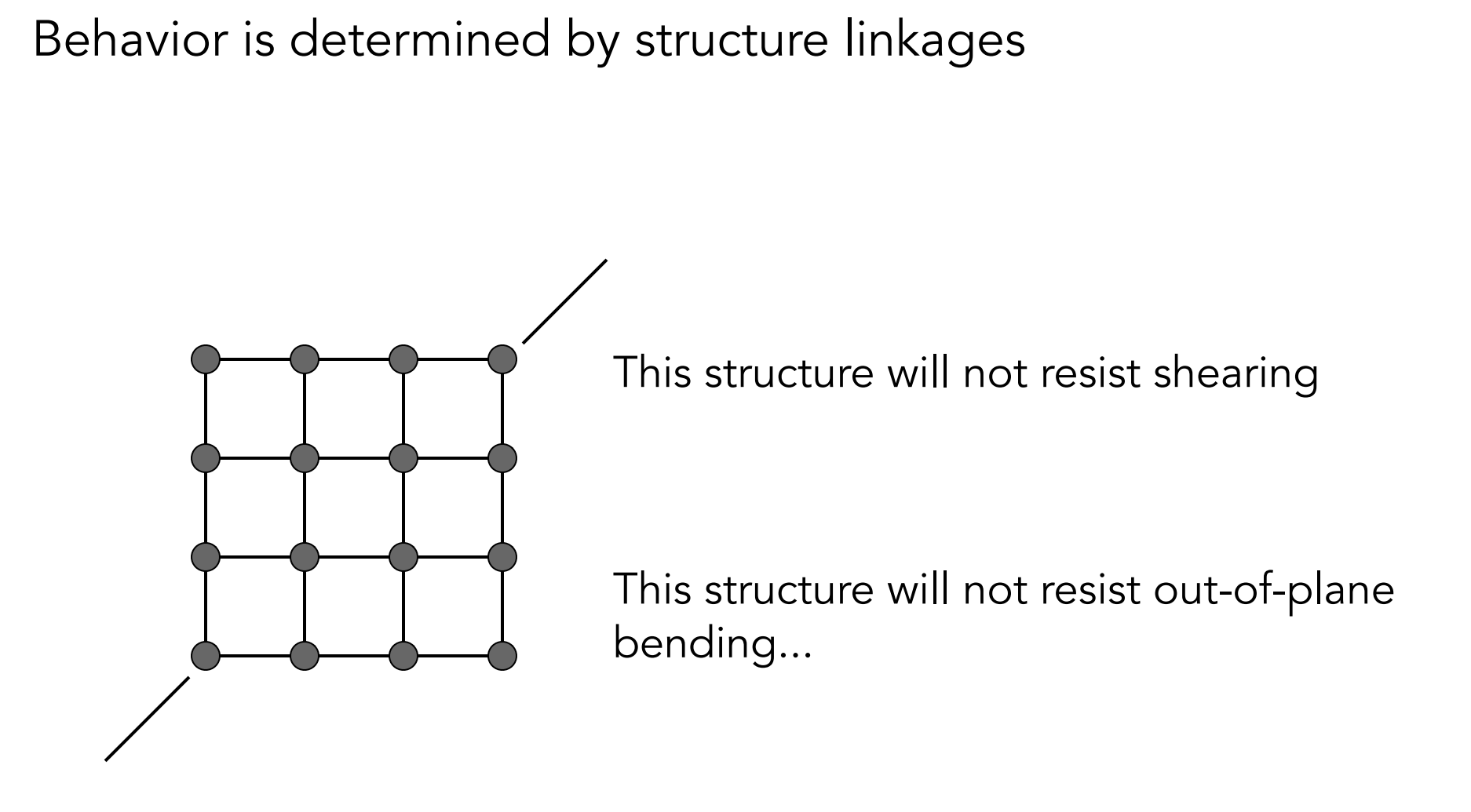
但是无法表现剪切力(如对角线拉布,布基本形状不变)、弯曲力(out-of-plane,抗拒被像纸一样完全折叠为两个三角形)等
加入两条对角线,以及skip connection
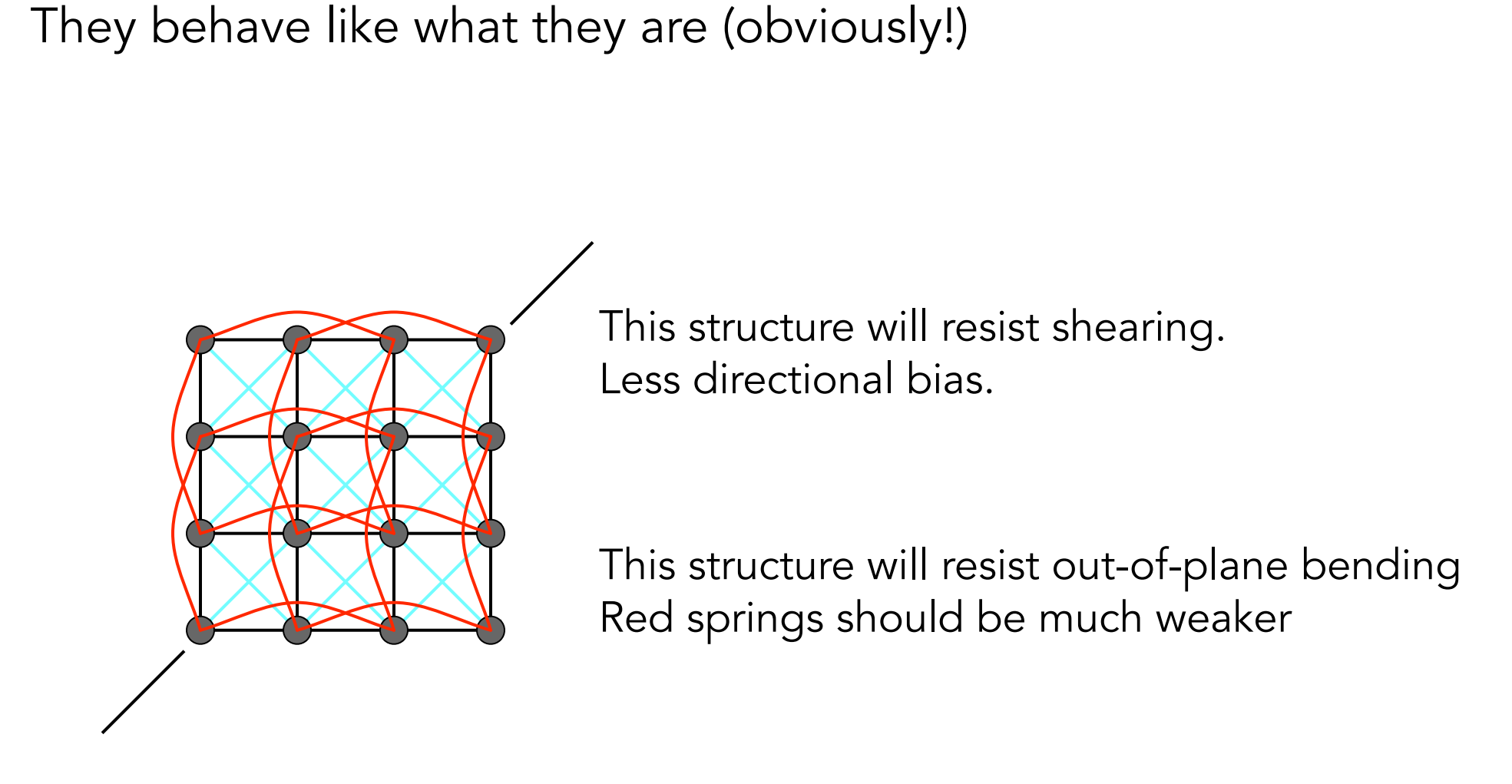
- 红色较弱,仅其辅助作用;蓝色较强,其主要作用;
其他方式:FEM (Finite Element Method, 有限元) Instead of Springs,考虑力传导
c.2). Particle System

- 粒子系统不仅可描述微小粒子,还可以描述一些群落;
d). Forward Kinematics(FK)
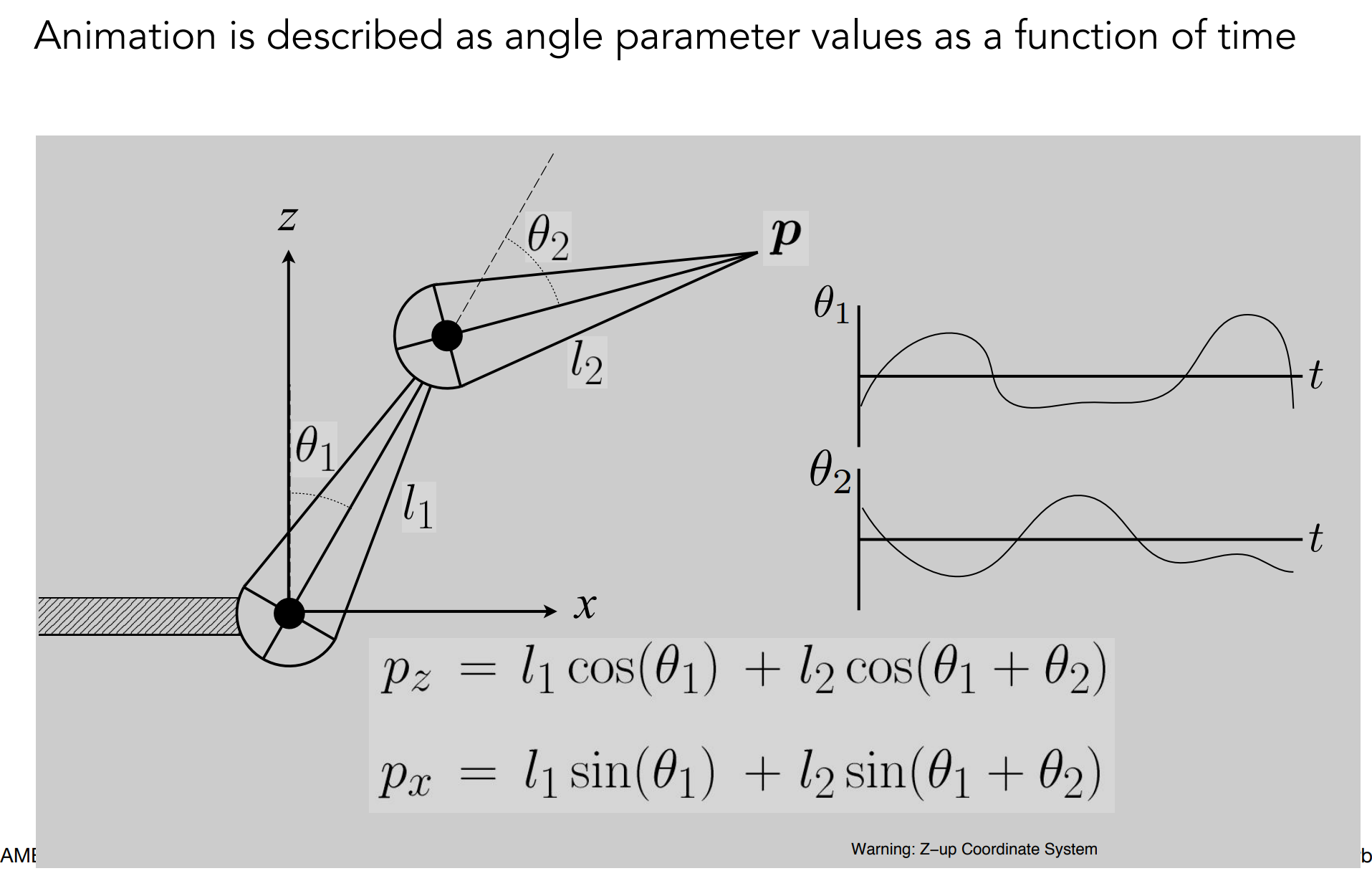
关节(Joint)分类:
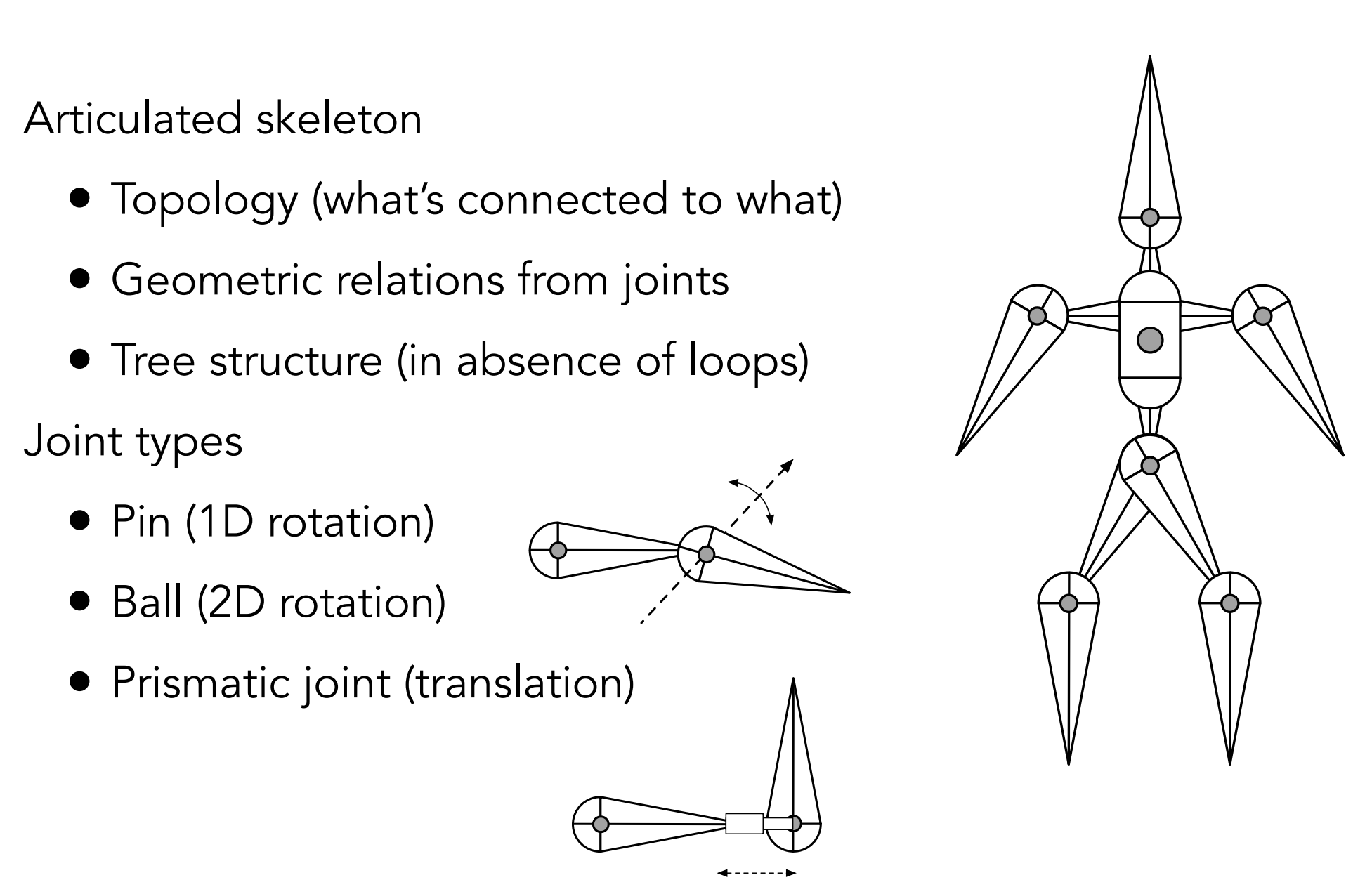
e). Inverse Kinematics(IK)
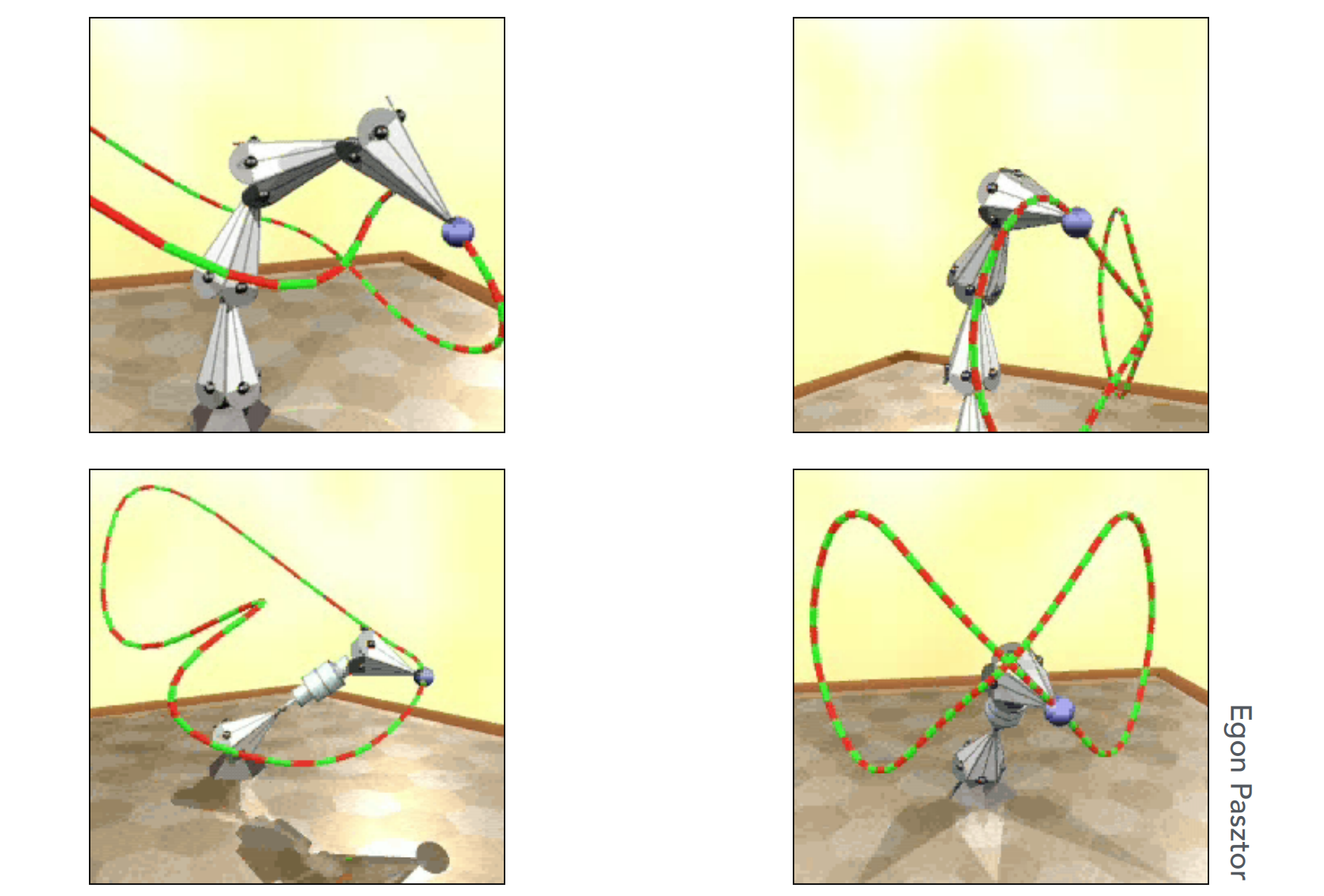

- 解决多个解的方法:梯度下降
f). Rigging

Blend shapes: 混合控制点或骨骼位置

g). Motion Capture / Facial Motion Capture
Games101-13-16 RayTracing
Lecture 13 Ray Tracing
a). vs. Rasterization
光栅化难以表现全局(global)效果,如
- (软)阴影(Soft shadows)
- 光线反弹超过一次(Glossy reflection)
- Indirect illumination(间接光照)

Rasterization is fast, but quality is relatively low;

b.). Basic Ray-Tracing Algorithm
光追中光线的性质:
- 光是沿直线传播的;
- 光相交时,并不产生干扰;
- 光从光源出发,传播到眼睛(由于光路可逆,也可是光线从眼睛出发,传播到光源)

b.1). Ray Casting
做法:
- Generate an image by casting one ray per pixel;(生成从眼睛出发的光线)
- Check for shadows by sending a ray to the light;(检查光线投射点是否可传播到光源)
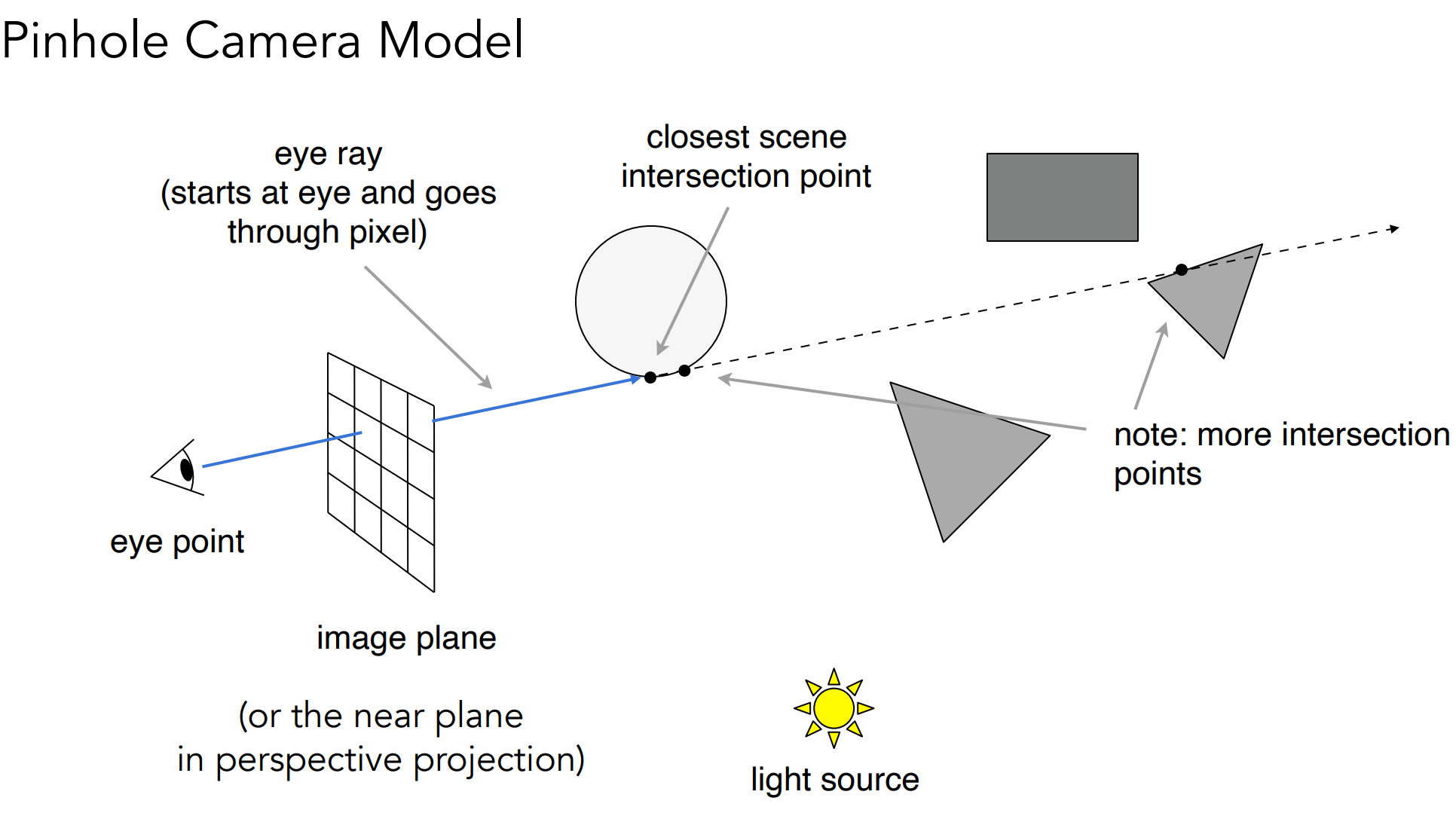
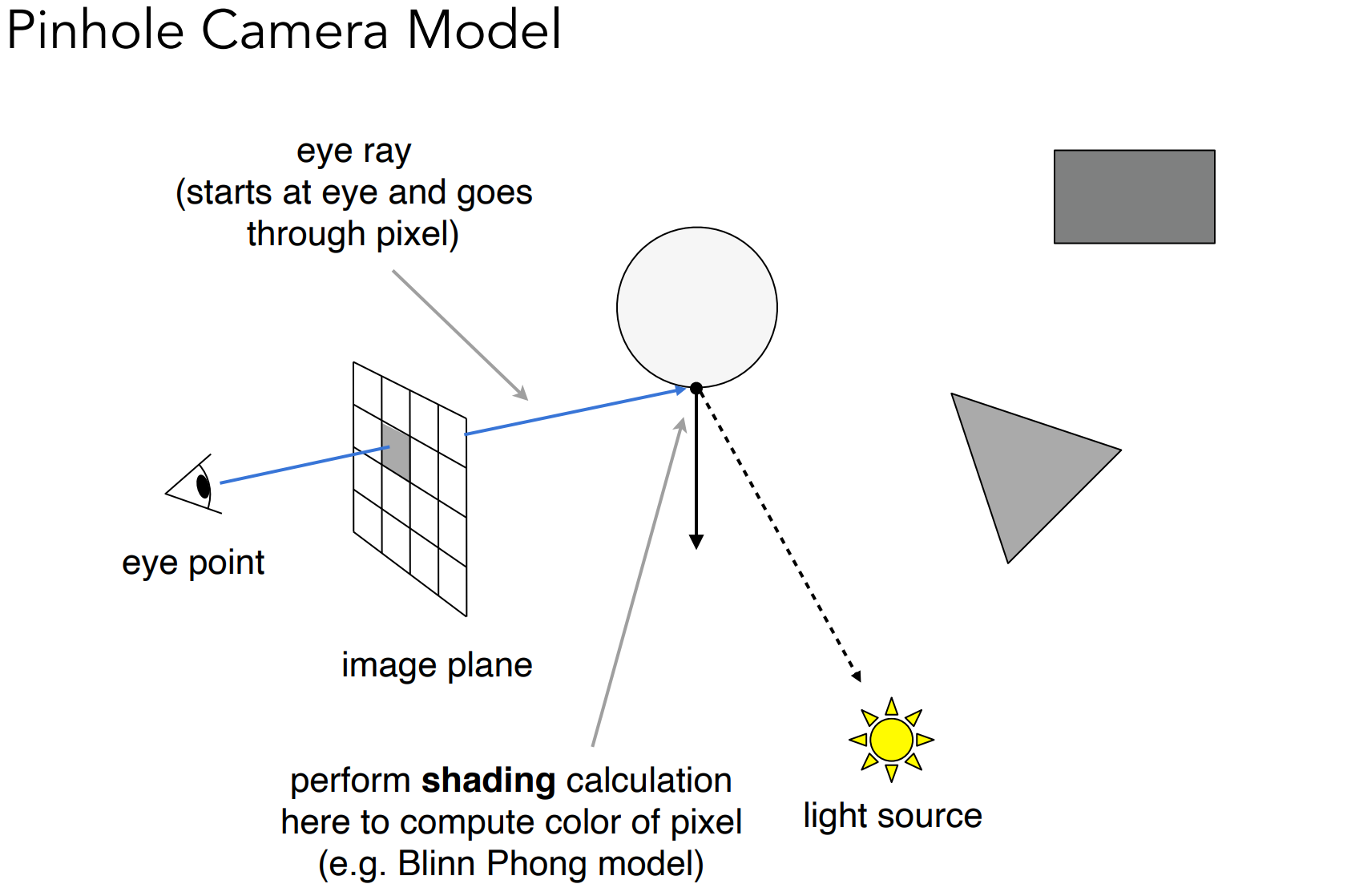
- 光线由眼睛出发,可不再使用深度缓存;
- 投射点到光源发射Shadow Ray,查看该点是否在阴影里(是否对光源可见);
Games101_10_12 Geometry
Games101-7-9 Shading
Lecture 07/08 Shading(Illumination, Shading and Graphics Pipeline)
a). Definition

b). A Simple Shading Model(Blinn-Phong Reflectance Model)
b.1). Fundamental
Blinn-Phong是一个经验模型,并不是严格基于物理的;
进入视线内的光照一般有以下构成:
- 高光(Specualr)
- 漫反射(Diffuse)
- 环境光(Ambient)
- 自发光(Emissive)
Shading is Local: Compute light reflected toward camera at a specific shading point
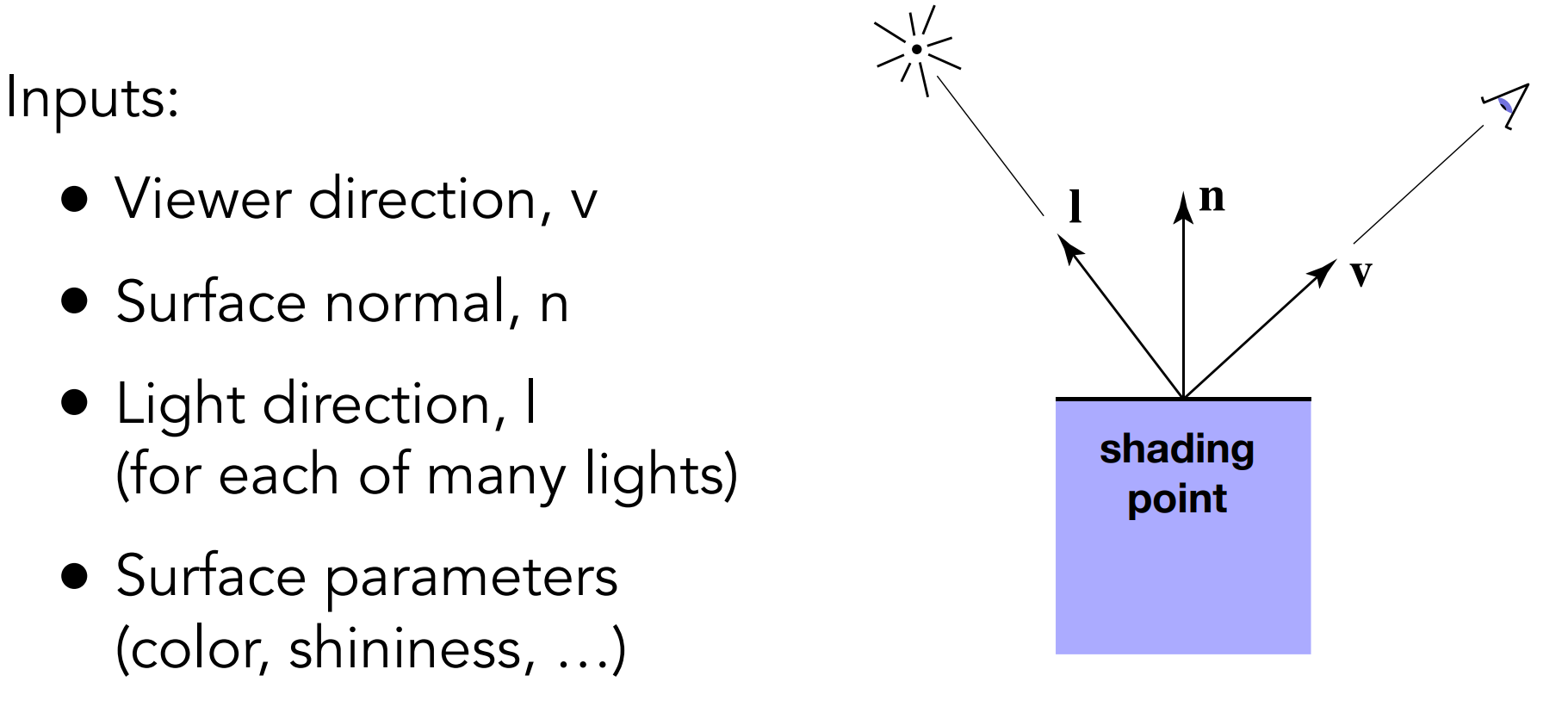
No shadows will be generated! (shading ≠ shadow)
- 阴影会由另外的Shadow Caster来着色;

b.2). Diffuse Reflection
- Blinn-Phong中,漫反射的光均匀散射到各个方向;
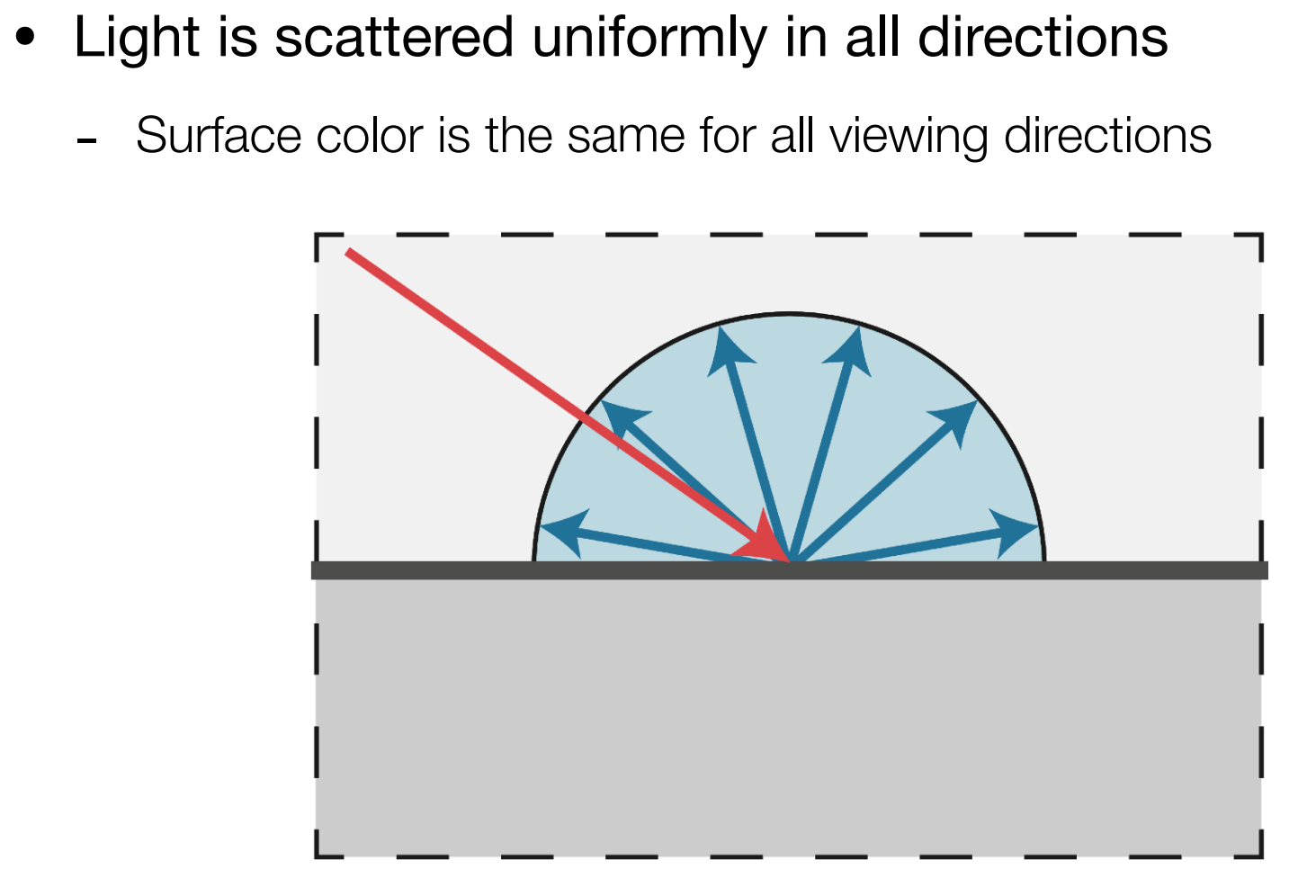
Lambert’s cosine law:接收到的能量与 $l·n$ 成正比例
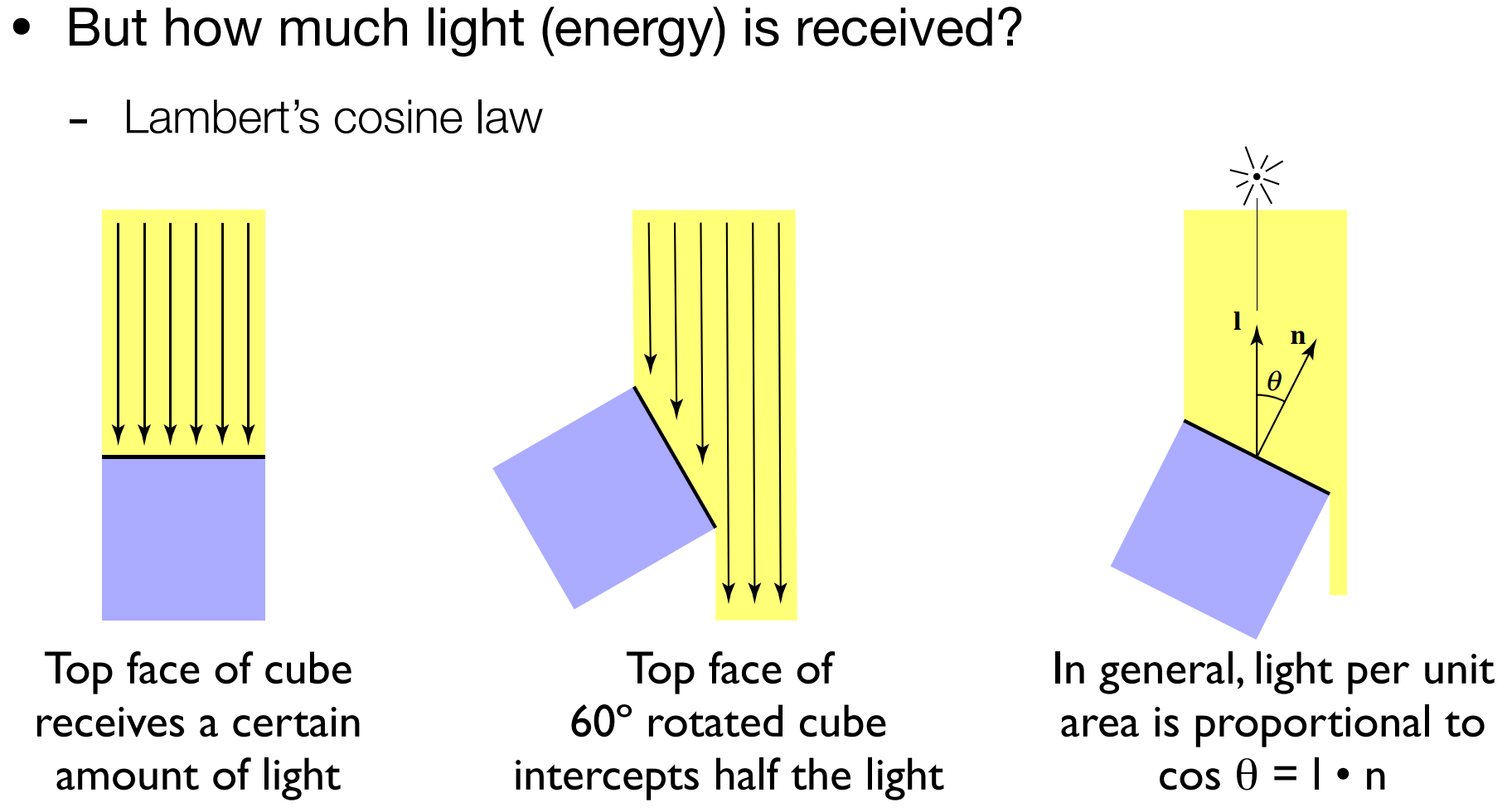
Light Falloff
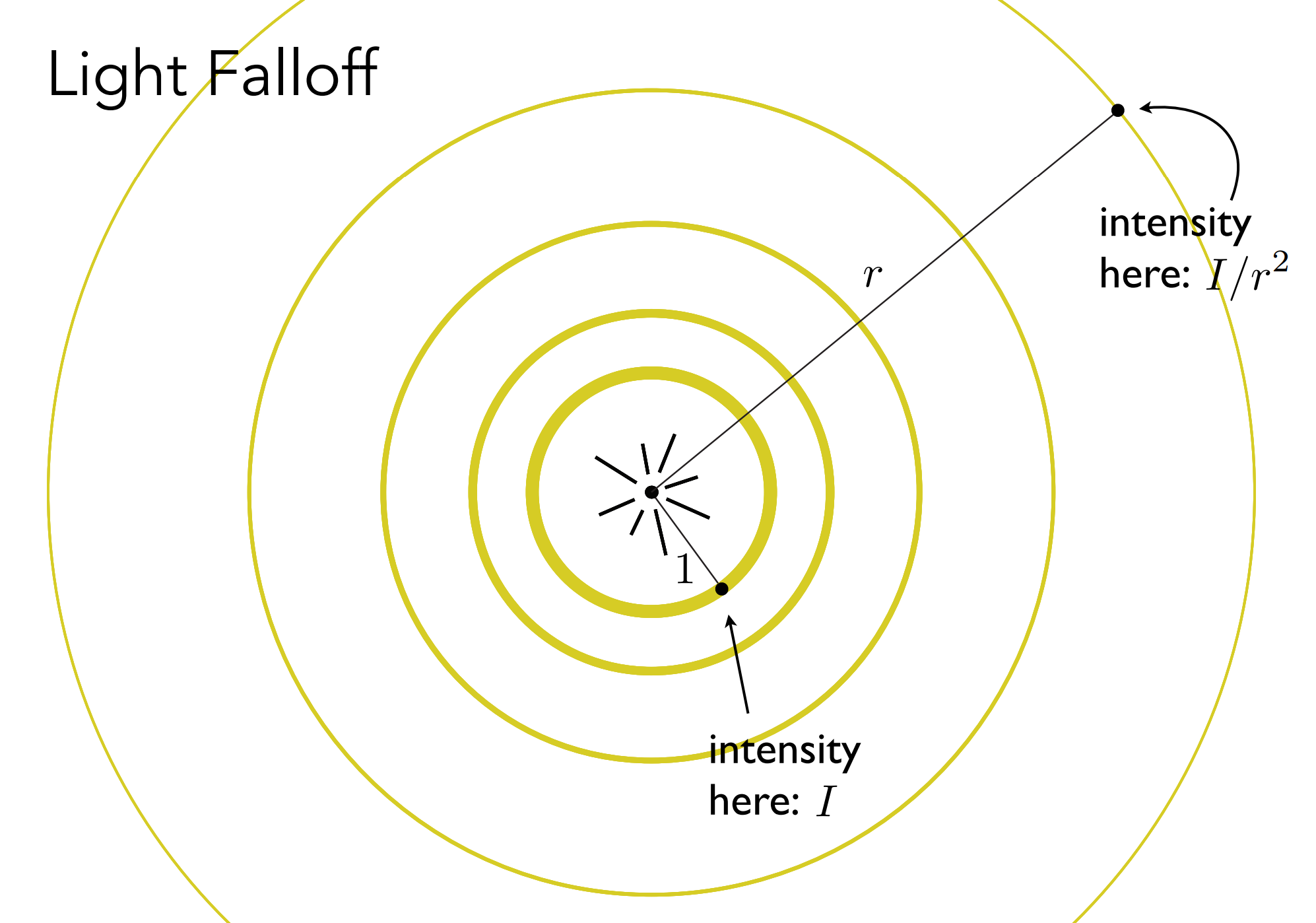
漫反射最终的着色:
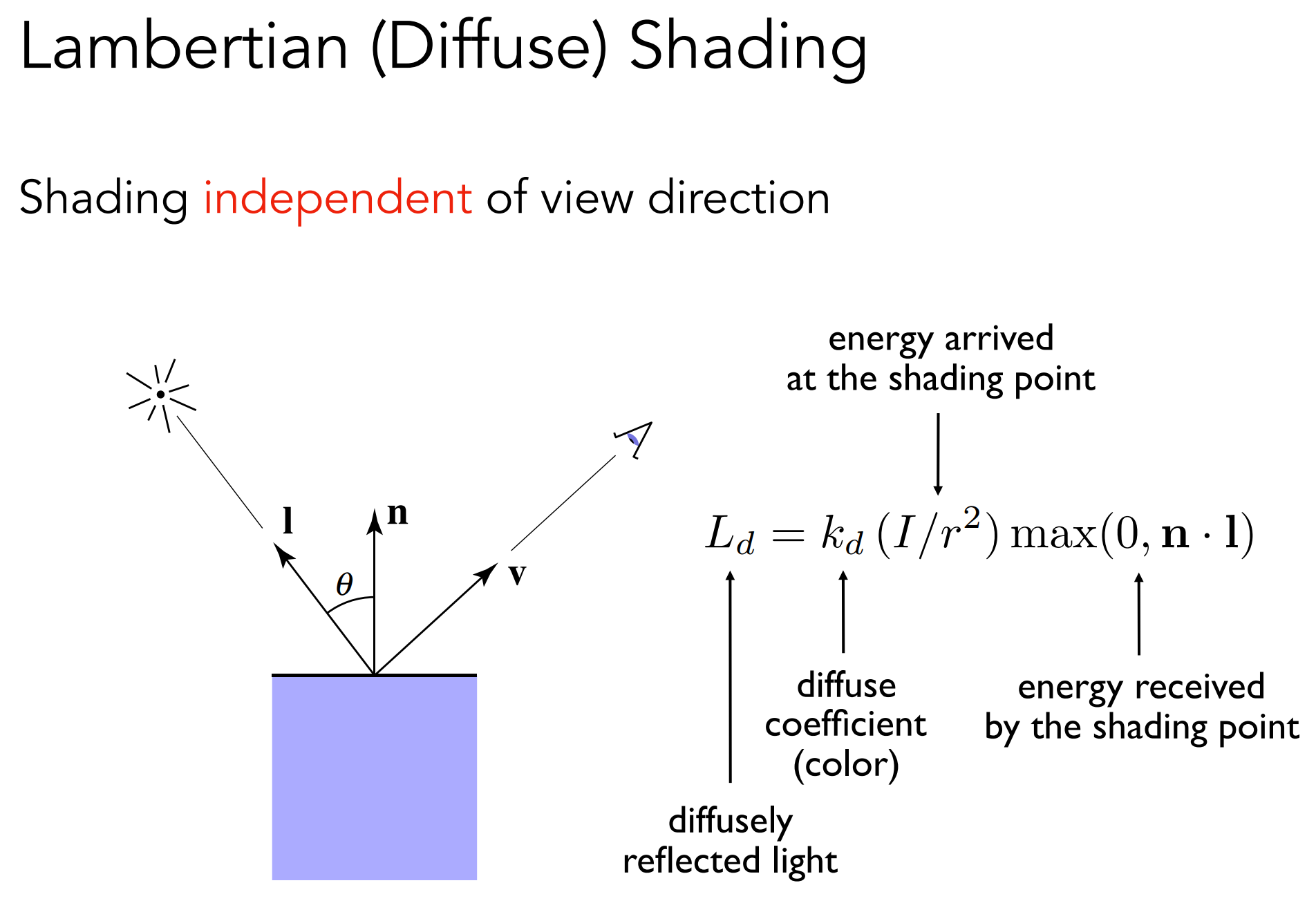

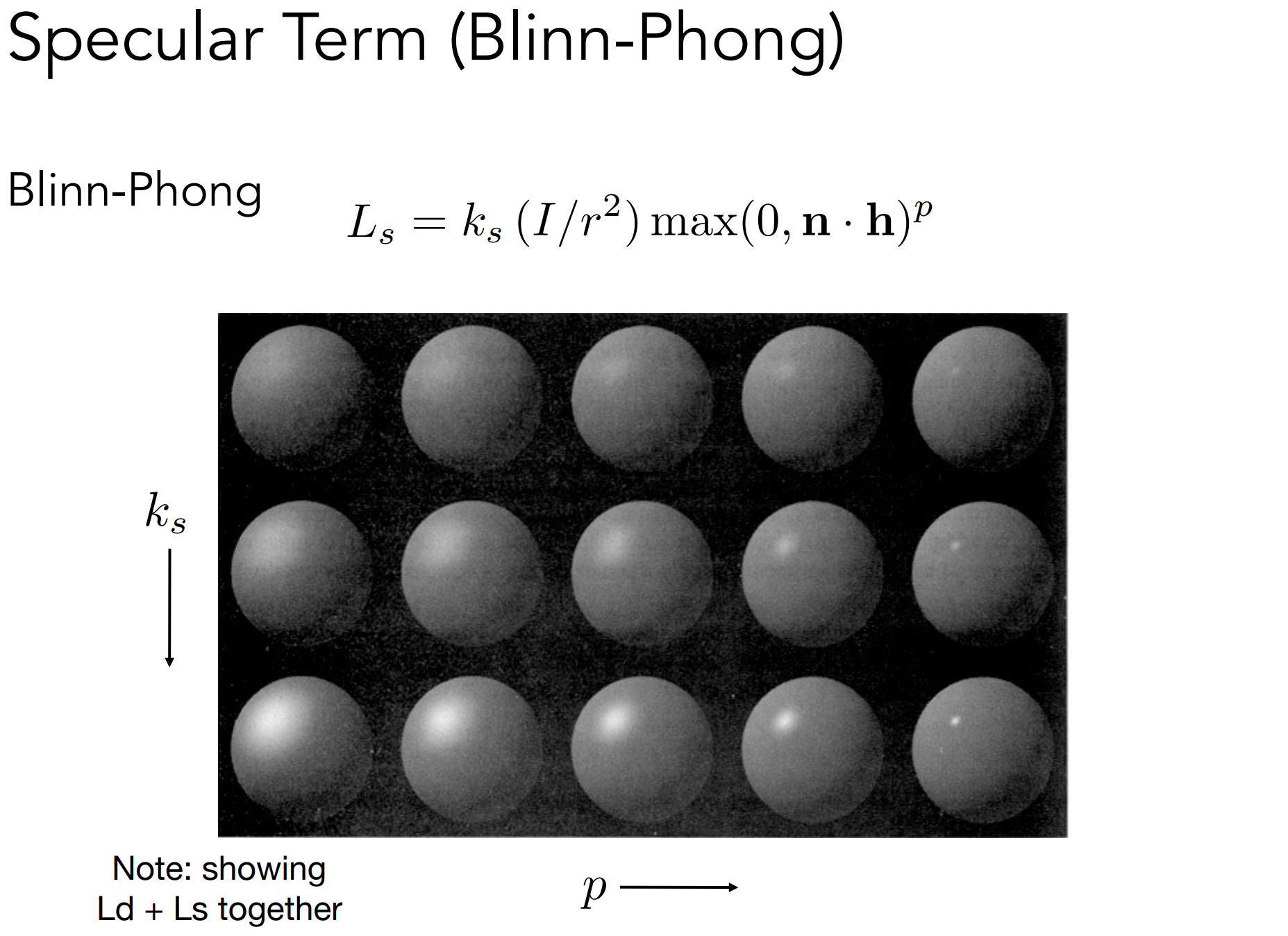
b.3). Specular Term(Blinn-Phong)
Intensity depends on view direction
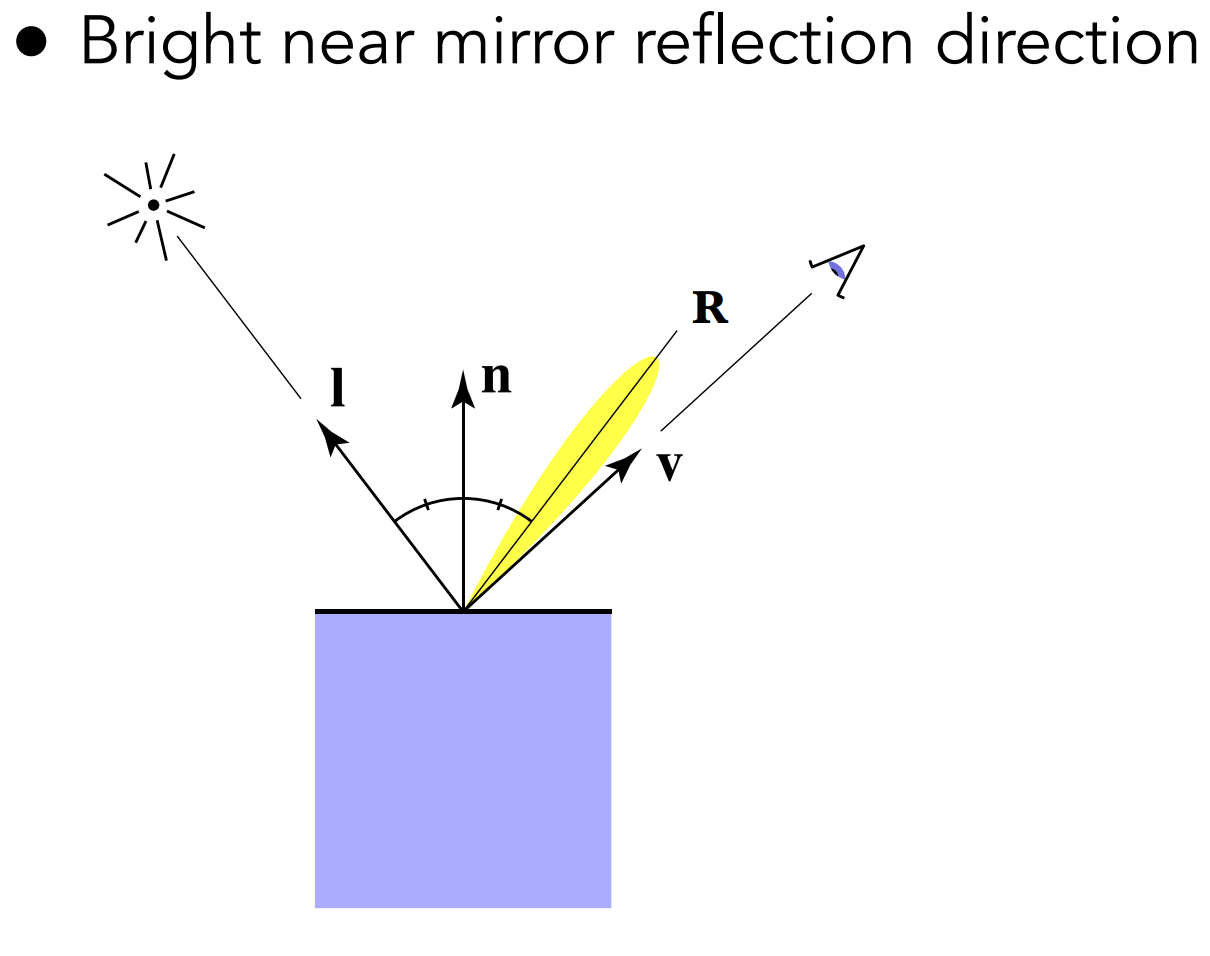
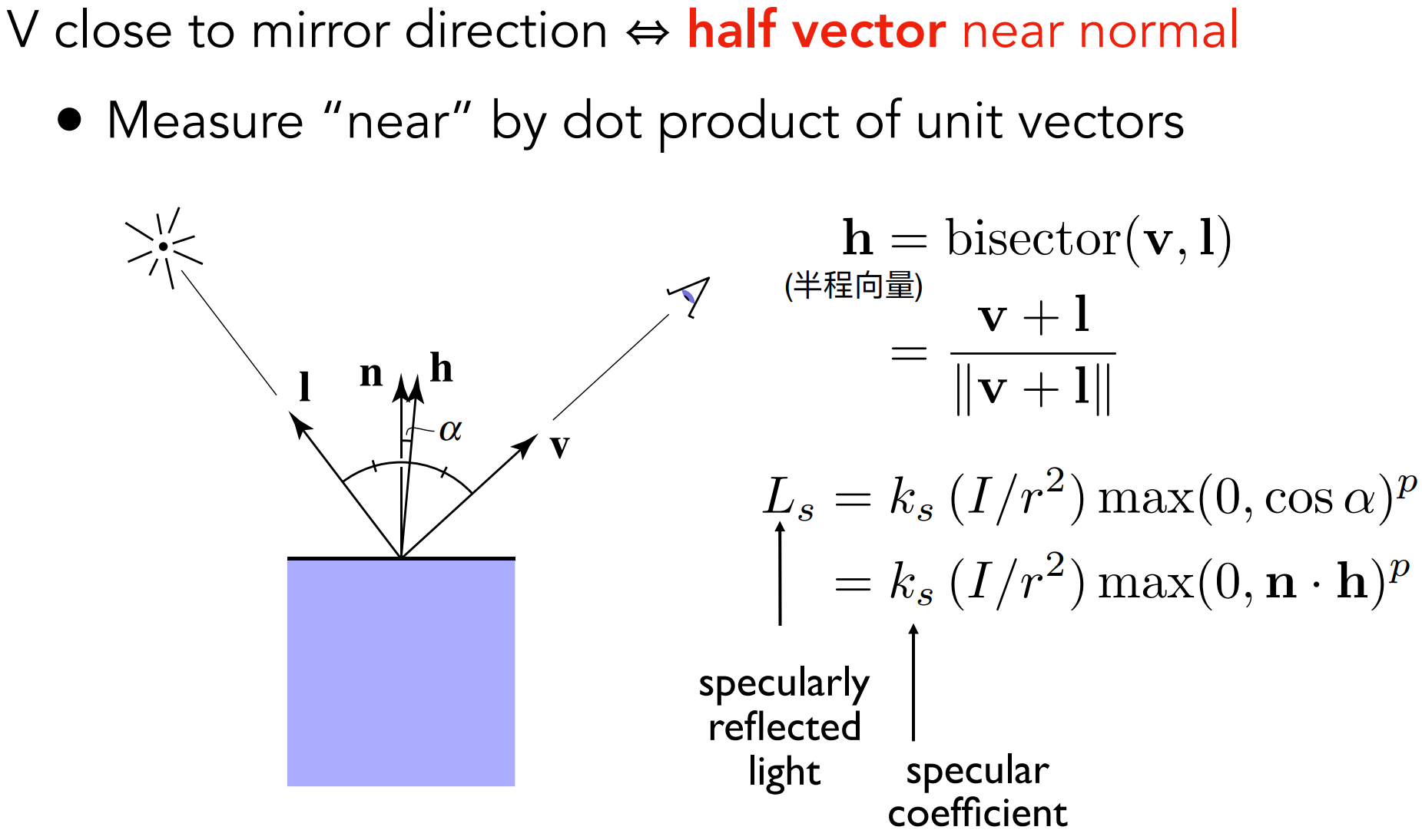
- 采用半程向量简化计算。采用半程向量$h$与$n$点乘的是Blinn-Phong模型,而采用镜面反射方向$r$和视线方向$v$点乘的是Phong模型;
- 指数$p$的作用:Increasing p narrows the reflection lobe
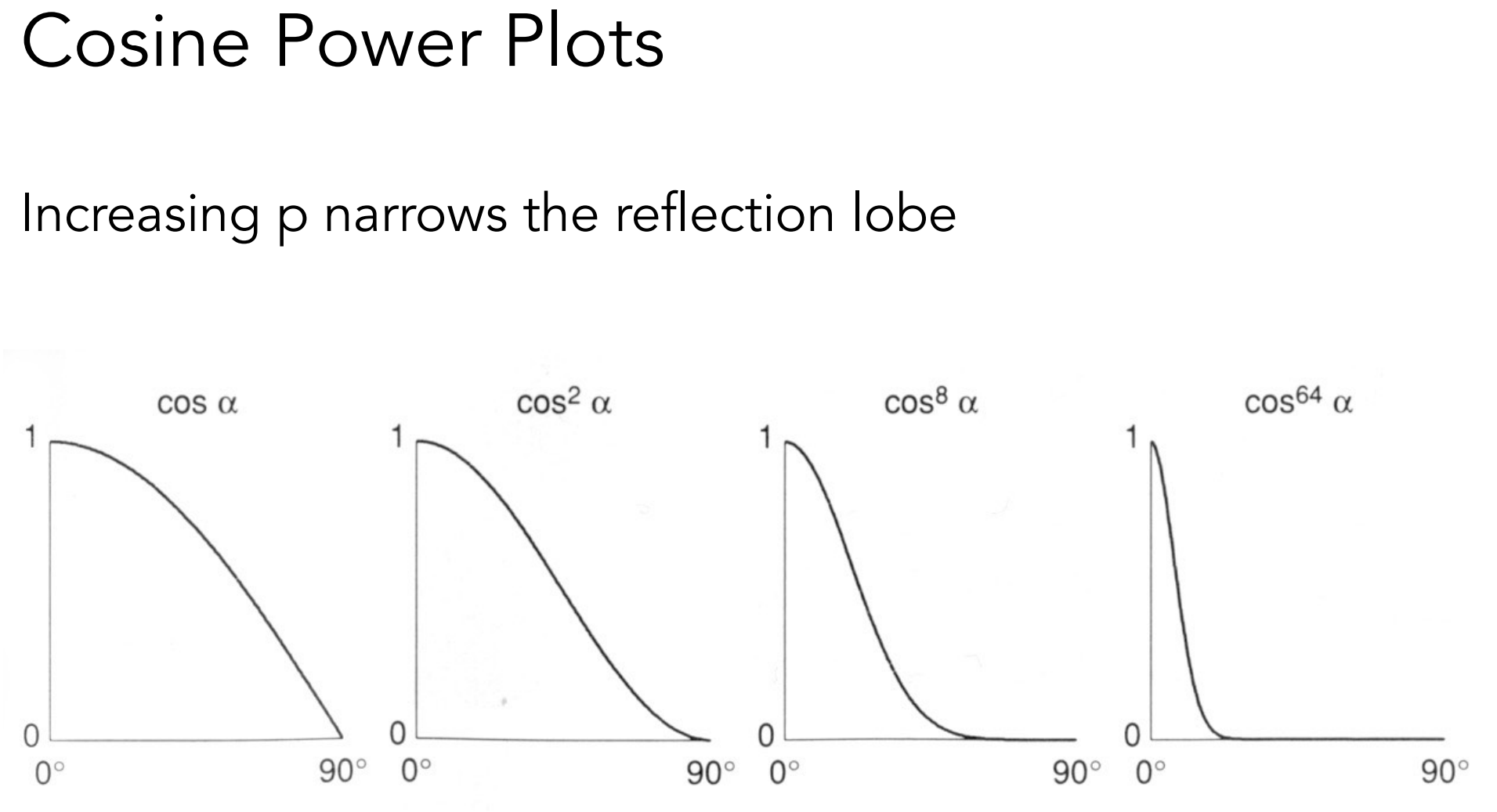
- 效果总览:
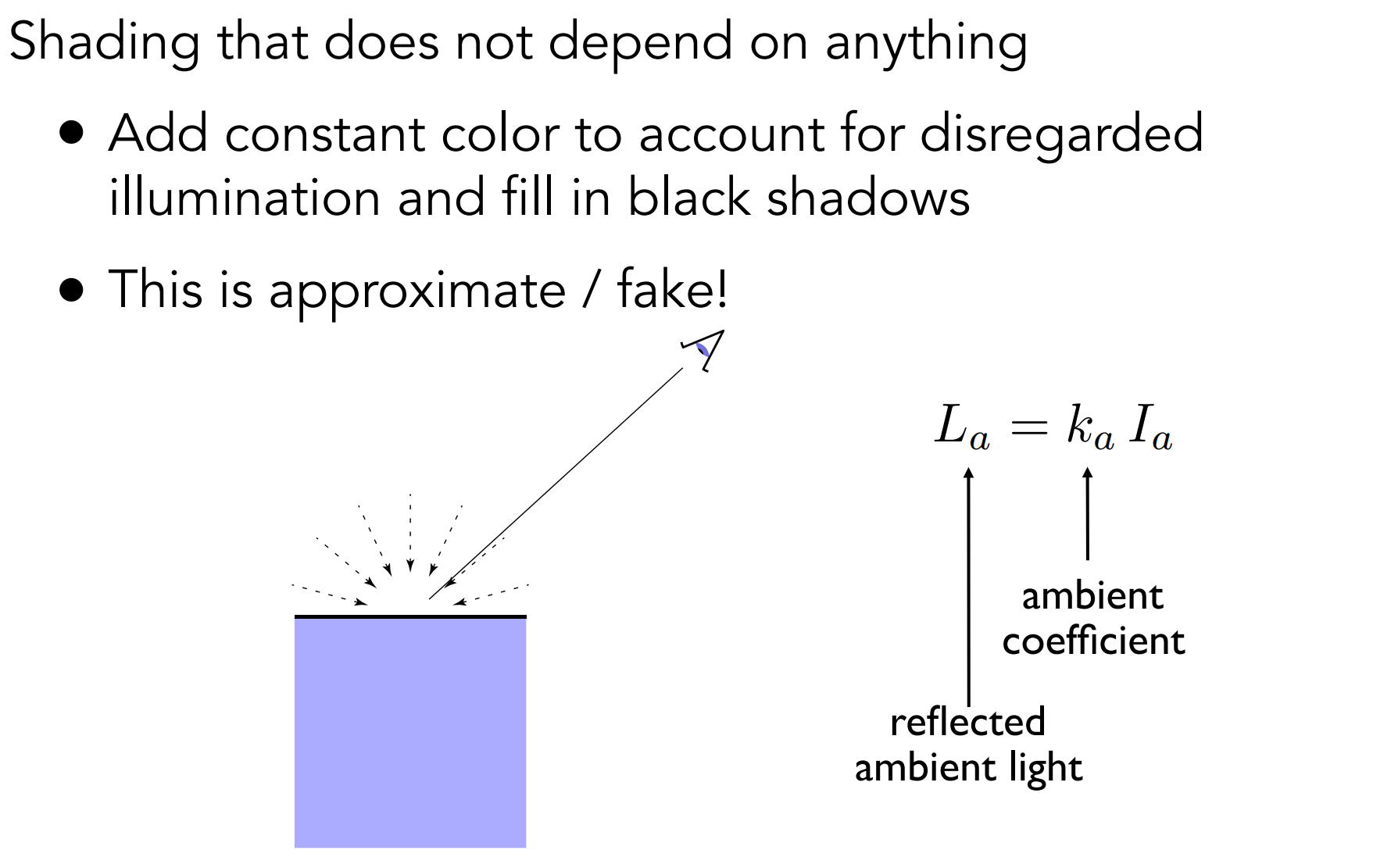
b.4). Ambient Term